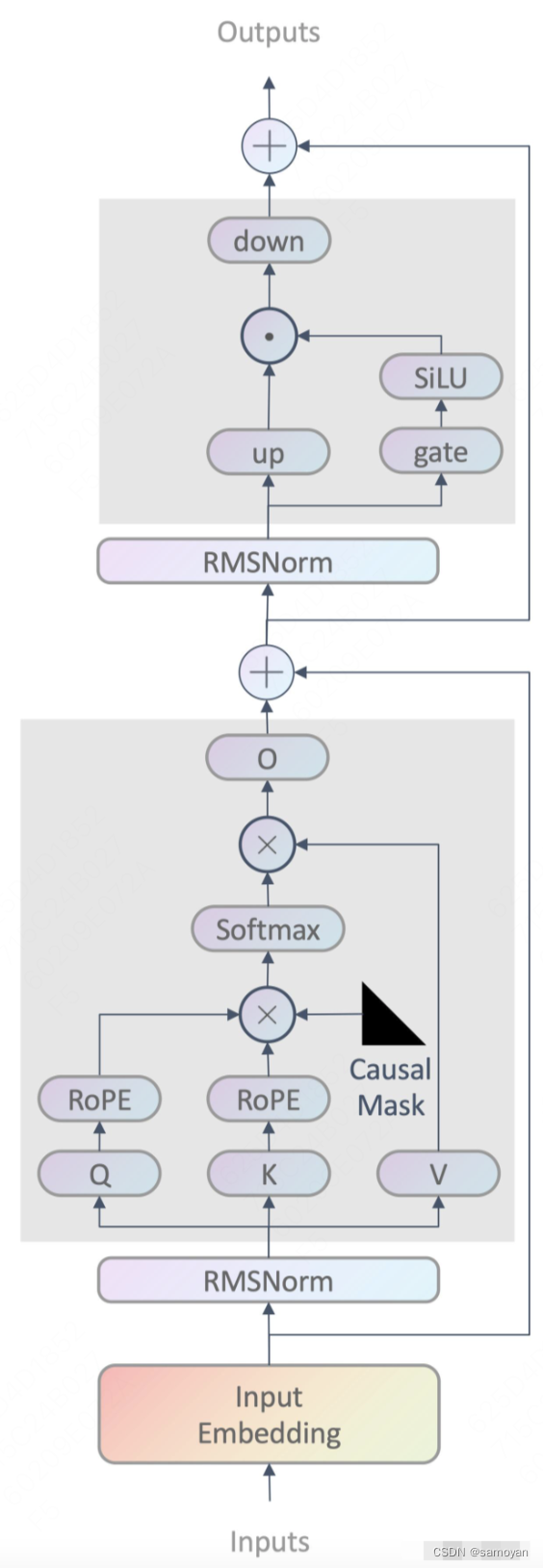
1. 最大熵原理
学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型。
假设离散随机变量X的概率分布是P(X),则其熵为
且满足0<=H(P)<=logN
当且仅当X的分布是均匀分布时右边的等号成立,即当X服从均匀分布时,熵最大。
直观地,最大熵原理认为要选择地概率模型首先必须满足已有事实(约束条件)。在没有更多信息的情况下,那些不确定的部分都是“等可能的”。
2. 最大熵模型的定义与学习
2.1 最大熵模型的定义
假设满足所有约束条件的模型集合为C,定义在条件概率分布P(Y|X)上的条件熵为
2.2 最大熵模型学的学习
其学习过程就是求解最大熵模型的过程,可以形式化为约束最优化问题。
最大熵模型与LR模型有类似的形式,它们又称为对数线性模型。这类模型的学习就是在给定训练数据条件下对模型进行极大似然估计或正则化的极大似然估计。
3. 模型学习的最优化方法
LR回归模型和最大熵模型学习归结为以似然函数为目标函数的(无约束)最优化问题,一般通过
迭代算法求解,这时的目标函数具有很好的性质(光滑的凸函数),多种最优化方法都适用,保证能找到全局最优解。
常用的方法有改进的迭代尺度法、梯度下降法、牛顿法或拟牛顿法。其中牛顿法或拟牛顿法一般收敛速度更快。
原文地址:https://blog.csdn.net/MusicDancing/article/details/134684586
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_11001.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!