智能优化算法 | Matlab实现金豺优化算法（GJO）（内含完整源码）

效果一览

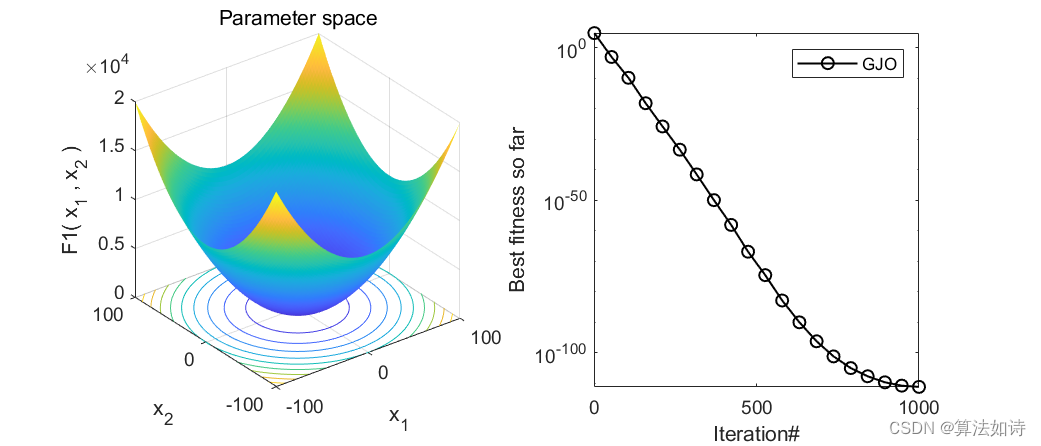
文章概述

智能优化算法 | Matlab实现金豺优化算法（GJO）（内含完整源码）

源码设计

%%

clear
clc
close
SearchAgents_no=30; % Number of search agents
Max_iteration=1000; % Maximum numbef of iterations

Function_name='F1';


%% Load details of the selected engineering design problem
[lb,ub,dim,fobj]=fun_info(Function_name);
[Male_Jackal_score,Male_Jackal_pos,GJO_cg_curve]=GJO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);


%%

display(['The best solution obtained by GJO for ' [num2str(Function_name)],'  is : ', num2str(Male_Jackal_pos)]);
display(['The best optimal value of the objective funciton found by GJO  for ' [num2str(Function_name)],'  is : ', num2str(Male_Jackal_score)]);

figure('Position',[454   445   694   297]);
subplot(1,2,1);
func_plot(Function_name);     % Function plot
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
subplot(1,2,2);       % Convergence plot

CNT=20;
k=round(linspace(1,Max_iteration,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:Max_iteration;
if ~strcmp(Function_name,'F16')&&~strcmp(Function_name,'F9')&&~strcmp(Function_name,'F11')  %这里是因为这几个函数收敛太快，不适用于semilogy，直接plot
    semilogy(iter(k),GJO_cg_curve(k),'k-o','linewidth',1);
else
    plot(iter(k),GJO_cg_curve(k),'k-o','linewidth',1);
end

xlabel('Iteration#');
ylabel('Best fitness so far');
legend('GJO');

%%


function [z] = levy(n,m,beta)

    num = gamma(1+beta)*sin(pi*beta/2); % used for Numerator 
    
    den = gamma((1+beta)/2)*beta*2^((beta-1)/2); % used for Denominator

    sigma_u = (num/den)^(1/beta);% Standard deviation

    u = random('Normal',0,sigma_u,n,m); 
    
    v = random('Normal',0,1,n,m);

    z =u./(abs(v).^(1/beta));

  
  end

%%


function X=initialization(SearchAgents_no,dim,ub,lb)

Boundary_no= size(ub,2); % numnber of boundaries

% If the boundaries of all variables are equal and user enter a signle
% number for both ub and lb
if Boundary_no==1
    X=rand(SearchAgents_no,dim).*(ub-lb)+lb;
end

% If each variable has a different lb and ub
if Boundary_no>1
    for i=1:dim
        ub_i=ub(i);
        lb_i=lb(i);
        X(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
    end
end

%%

function [Male_Jackal_score,Male_Jackal_pos,Convergence_curve]=GJO(SearchAgents_no,Max_iter,lb,ub,dim,fobj)

%% initialize Golden jackal pair
Male_Jackal_pos=zeros(1,dim);
Male_Jackal_score=inf; 
Female_Jackal_pos=zeros(1,dim);  
Female_Jackal_score=inf; 

%% Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iter);

l=0;% Loop counter

% Main loop
while l<Max_iter
        for i=1:size(Positions,1)  

           % boundary checking
            Flag4ub=Positions(i,:)>ub;
            Flag4lb=Positions(i,:)<lb;
            Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;               

            % Calculate objective function for each search agent
            fitness=fobj(Positions(i,:));

            % Update Male Jackal 
            if fitness<Male_Jackal_score 
                Male_Jackal_score=fitness; 
                Male_Jackal_pos=Positions(i,:);
            end  
             if fitness>Male_Jackal_score &amp;&amp; fitness<Female_Jackal_score 
                Female_Jackal_score=fitness; 
                Female_Jackal_pos=Positions(i,:);
            end
        end
    
    
    
     E1=1.5*(1-(l/Max_iter));
       RL=0.05*levy(SearchAgents_no,dim,1.5);
     
    for i=1:size(Positions,1)
        for j=1:size(Positions,2)     
                       
            r1=rand(); % r1 is a random number in [0,1]
            E0=2*r1-1;            
           E=E1*E0; % Evading energy
            
            
             if abs(E)<1
                %% EXPLOITATION
               D_male_jackal=abs((RL(i,j)*Male_Jackal_pos(j)-Positions(i,j))); 
                Male_Positions(i,j)=Male_Jackal_pos(j)-E*D_male_jackal;
                D_female_jackal=abs((RL(i,j)*Female_Jackal_pos(j)-Positions(i,j))); 
                Female_Positions(i,j)=Female_Jackal_pos(j)-E*D_female_jackal;
                
            else
                %% EXPLORATION
               D_male_jackal=abs( (Male_Jackal_pos(j)- RL(i,j)*Positions(i,j)));
                Male_Positions(i,j)=Male_Jackal_pos(j)-E*D_male_jackal;
              D_female_jackal=abs( (Female_Jackal_pos(j)- RL(i,j)*Positions(i,j)));
                Female_Positions(i,j)=Female_Jackal_pos(j)-E*D_female_jackal;
             end
             Positions(i,j)=(Male_Positions(i,j)+Female_Positions(i,j))/2;

                                
        end
    end
    l=l+1;    
        
    Convergence_curve(l)=Male_Jackal_score;
end

%%

function func_plot(func_name)

[LB,UB,Dim,F_obj]=fun_info(func_name);

switch func_name 
    case 'F1' 
        x=-100:2:100; y=x; %[-100,100]
        
    case 'F2' 
        x=-100:2:100; y=x; %[-10,10]
        
    case 'F3' 
        x=-100:2:100; y=x; %[-100,100]
        
    case 'F4' 
        x=-100:2:100; y=x; %[-100,100]
    case 'F5' 
        x=-200:2:200; y=x; %[-5,5]
    case 'F6' 
        x=-100:2:100; y=x; %[-100,100]
    case 'F7' 
        x=-1:0.03:1;  y=x  %[-1,1]
    case 'F8' 
        x=-500:10:500;y=x; %[-500,500]
    case 'F9' 
        x=-5:0.1:5;   y=x; %[-5,5]    
    case 'F10' 
        x=-20:0.5:20; y=x;%[-500,500]
    case 'F11' 
        x=-500:10:500; y=x;%[-0.5,0.5]
    case 'F12' 
        x=-10:0.1:10; y=x;%[-pi,pi]
    case 'F13' 
        x=-5:0.08:5; y=x;%[-3,1]
    case 'F14' 
        x=-100:2:100; y=x;%[-100,100]
    case 'F15' 
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F16' 
        x=-1:0.01:1; y=x;%[-5,5]
    case 'F17' 
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F18' 
        x=-5:0.06:5; y=x;%[-5,5]
    case 'F19' 
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F20' 
        x=-5:0.1:5; y=x;%[-5,5]        
    case 'F21' 
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F22' 
        x=-5:0.1:5; y=x;%[-5,5]     
    case 'F23' 
        x=-5:0.1:5; y=x;%[-5,5]  
end    

    

L=length(x);
f=[];

for i=1:L
    for j=1:L
        if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
            f(i,j)=F_obj([x(i),y(j)]);
        end
        if strcmp(func_name,'F15')==1
            f(i,j)=F_obj([x(i),y(j),0,0]);
        end
        if strcmp(func_name,'F19')==1
            f(i,j)=F_obj([x(i),y(j),0]);
        end
        if strcmp(func_name,'F20')==1
            f(i,j)=F_obj([x(i),y(j),0,0,0,0]);
        end       
        if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
            f(i,j)=F_obj([x(i),y(j),0,0]);
        end          
    end
end

surfc(x,y,f,'LineStyle','none');

end

%%

function [lowerbound,upperbound,dimension,fitness] = fun_info(F)


switch F
    case 'F1'
        fitness = @F1;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F2'
        fitness = @F2;
        lowerbound=-10;
        upperbound=10;
        dimension=30;
        
    case 'F3'
        fitness = @F3;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F4'
        fitness = @F4;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F5'
        fitness = @F5;
        lowerbound=-30;
        upperbound=30;
        dimension=30;
        
    case 'F6'
        fitness = @F6;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F7'
        fitness = @F7;
        lowerbound=-1.28;
        upperbound=1.28;
        dimension=30;
        
    case 'F8'
        fitness = @F8;
        lowerbound=-500;
        upperbound=500;
        dimension=30;
        
    case 'F9'
        fitness = @F9;
        lowerbound=-5.12;
        upperbound=5.12;
        dimension=30;
        
    case 'F10'
        fitness = @F10;
        lowerbound=-32;
        upperbound=32;
        dimension=30;
        
    case 'F11'
        fitness = @F11;
        lowerbound=-600;
        upperbound=600;
        dimension=30;
        
    case 'F12'
        fitness = @F12;
        lowerbound=-50;
        upperbound=50;
        dimension=30;
        
    case 'F13'
        fitness = @F13;
        lowerbound=-50;
        upperbound=50;
        dimension=30;
        
    case 'F14'
        fitness = @F14;
        lowerbound=-65.536;
        upperbound=65.536;
        dimension=2;
        
    case 'F15'
        fitness = @F15;
        lowerbound=-5;
        upperbound=5;
        dimension=4;
        
    case 'F16'
        fitness = @F16;
        lowerbound=-5;
        upperbound=5;
        dimension=2;
        
    case 'F17'
        fitness = @F17;
        lowerbound=[-5,0];
        upperbound=[10,15];
        dimension=2;
        
    case 'F18'
        fitness = @F18;
        lowerbound=-2;
        upperbound=2;
        dimension=2;
        
    case 'F19'
        fitness = @F19;
        lowerbound=0;
        upperbound=1;
        dimension=3;
        
    case 'F20'
        fitness = @F20;
        lowerbound=0;
        upperbound=1;
        dimension=6;     
        
    case 'F21'
        fitness = @F21;
        lowerbound=0;
        upperbound=10;
        dimension=4;    
        
    case 'F22'
        fitness = @F22;
        lowerbound=0;
        upperbound=10;
        dimension=4;    
        
    case 'F23'
        fitness = @F23;
        lowerbound=0;
        upperbound=10;
        dimension=4;            
end

end

% F1

function R = F1(x)
R=sum(x.^2);
end

% F2

function R = F2(x)
R=sum(abs(x))+prod(abs(x));
end

% F3

function R = F3(x)
dimension=size(x,2);
R=0;
for i=1:dimension
    R=R+sum(x(1:i))^2;
end
end

% F4

function R = F4(x)
R=max(abs(x));
end

% F5

function R = F5(x)
dimension=size(x,2);
R=sum(100*(x(2:dimension)-(x(1:dimension-1).^2)).^2+(x(1:dimension-1)-1).^2);
end

% F6

function R = F6(x)
R=sum(floor((x+.5)).^2);
end

% F7

function R = F7(x)
dimension=size(x,2);
R=sum([1:dimension].*(x.^4))+rand;
end

% F8

function R = F8(x)
R=sum(-x.*sin(sqrt(abs(x))));
end

% F9

function R = F9(x)
dimension=size(x,2);
R=sum(x.^2-10*cos(2*pi.*x))+10*dimension;
end

% F10

function R = F10(x)
dimension=size(x,2);
R=-20*exp(-.2*sqrt(sum(x.^2)/dimension))-exp(sum(cos(2*pi.*x))/dimension)+20+exp(1);
end

% F11

function R = F11(x)
dimension=size(x,2);
R=sum(x.^2)/4000-prod(cos(x./sqrt([1:dimension])))+1;
end

% F12

function R = F12(x)
dimension=size(x,2);
R=(pi/dimension)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dimension-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dimension)+1)./4)))).^2))+((x(dimension)+1)/4)^2)+sum(Ufun(x,10,100,4));
end

% F13

function R = F13(x)
dimension=size(x,2);
R=.1*((sin(3*pi*x(1)))^2+sum((x(1:dimension-1)-1).^2.*(1+(sin(3.*pi.*x(2:dimension))).^2))+...
((x(dimension)-1)^2)*(1+(sin(2*pi*x(dimension)))^2))+sum(Ufun(x,5,100,4));
end

% F14

function R = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];

for j=1:25
    bS(j)=sum((x'-aS(:,j)).^6);
end
R=(1/500+sum(1./([1:25]+bS))).^(-1);
end

% F15

function R = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
R=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end

% F16

function R = F16(x)
R=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end

% F17

function R = F17(x)
R=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end

% F18

function R = F18(x)
R=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
    (30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end

% F19

function R = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
R=0;
for i=1:4
    R=R-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end

% F20

function R = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
R=0;
for i=1:4
    R=R-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end

% F21

function R = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

R=0;
for i=1:5
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F22

function R = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

R=0;
for i=1:7
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F23

function R = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

R=0;
for i=1:10
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

function R=Ufun(x,a,k,m)
R=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end

参考资料

[1] https://blog.csdn.net/qq_59771180/article/details/131502581?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/qq_59771180/article/details/131503342?spm=1001.2014.3001.5502

代码007普通

打赏 收藏 海报 链接