【KNN算法详解（用法，优缺点，适用场景）及应用】

本文介绍: KNN（K Ne ar Ne i g h bor）：k个最近的邻居，即每个样本都可以用它最接近的k个邻居来代表。KNN算法属于监督学习方式的分类算法，我的理解就是计算某给点到每个点的距离作为相似度的反馈。简单来讲，KNN就是“近朱者赤，近墨者黑”的一种分类算法。KNN是一种基于实例的学习，属于懒惰学习，即没有显式学习过程。要区分一下聚类（如Kmeans等），KNN是监督学习分类，而Kmeans是无监督学习的聚类，聚类将无标签的数据分成不同的簇。

KNN算法介绍

KNN（K Near Nei g h bor）：k个最近的邻居，即每个样本都可以用它最接近的k个邻居来代表。KNN算法属于监督学习方式的分类算法，我的理解就是计算某给点到每个点的距离作为相似度的反馈。

简单来讲，KNN就是“近朱者赤，近墨者黑”的一种分类算法。
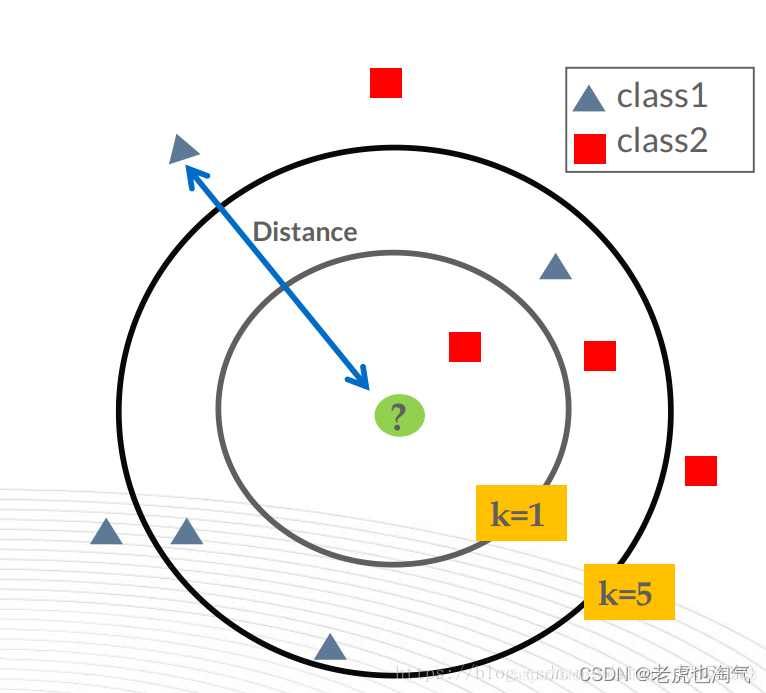
在这里插入图片描述

KNN是一种基于实例的学习，属于懒惰学习，即没有显式学习过程。

要区分一下聚类（如Kmeans等），KNN是监督学习分类，而Kmeans是无监督学习的聚类，聚类将无标签的数据分成不同的簇。
在这里插入图片描述

KNN算法三要素

距离度量

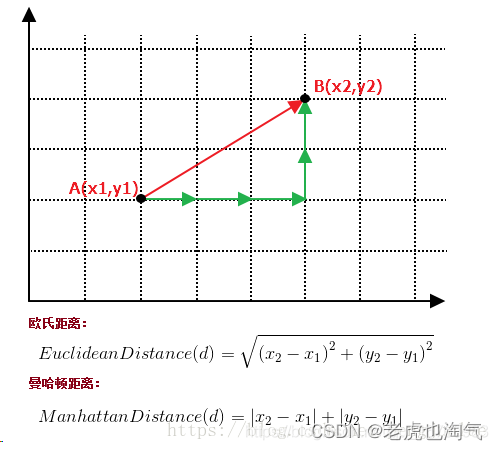
特征连续：距离函数选用曼哈顿距离（L1距离）/欧氏距离（L2距离）在这里插入图片描述
当p=1 的时候，它是曼哈顿距离
当p=2的时候，它是欧式距离
当p不选择的时候，它是切比雪夫
特征离散：汉明距离

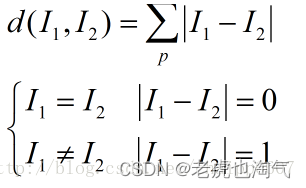
举最简单的例子来说明欧式/曼哈顿距离公式是什么样的。

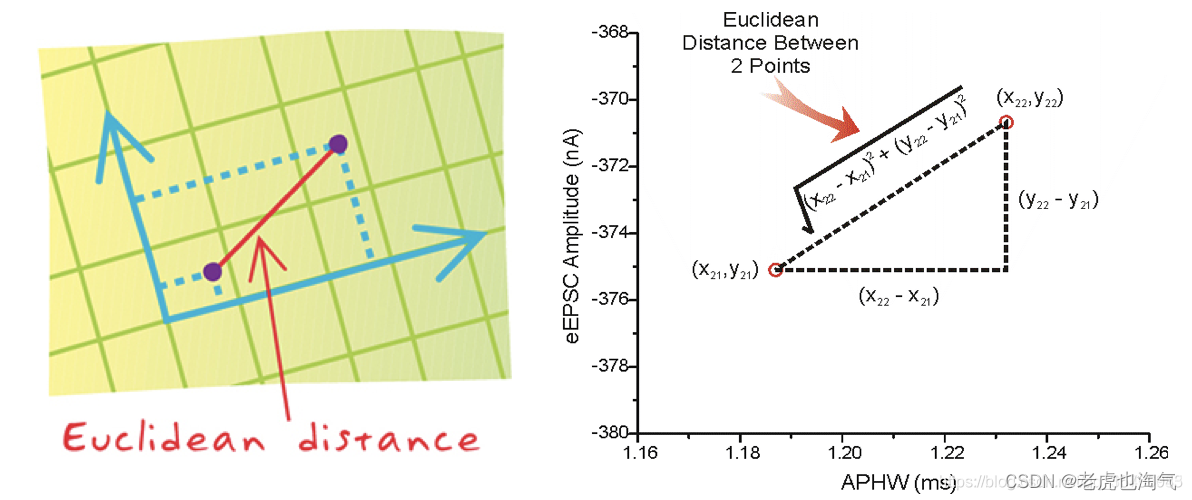
K取值

在sci kit-learn重KNN算法的K值是通过n_neighbors 参数来调节的，默认值是5。

参考李航博士一书统计学习方法中写道的K值选择：

K值小，相当于用较小的领域中的训练实例进行预测，只要与输入实例相近的实例才会对预测结果，模型变得复杂，只要改变一点点就可能导致分类结果出错，泛化性不佳。（学习近似误差小，但是估计误差增大，过拟合）
K值大，相当于用较大的领域中的训练实例进行预测，与输入实例较远的实例也会对预测结果产生影响，模型变得简单，可能预测出错。（学习近似误差大，但是估计误差小，欠拟合）
极端情况：K=0，没有可以类比的邻居；K=N，模型太简单，输出的分类就是所有类中数量最多的，距离都没有产生作用。
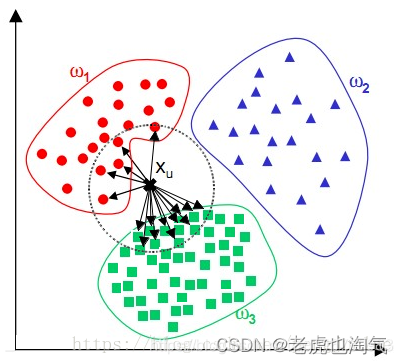
在这里插入图片描述
什么是近似误差和估计误差：

近似误差：训练集上的误差
估计误差：测试集上的误差

分类规则

knn 使用的分类决策规则是多数表决，如果损失函数为0-1损失函数，那么要使误分类率最小即使经验风险最小，多数表决规则实际上就等同于经验风险最小化。

KNN实际应用

案例引入
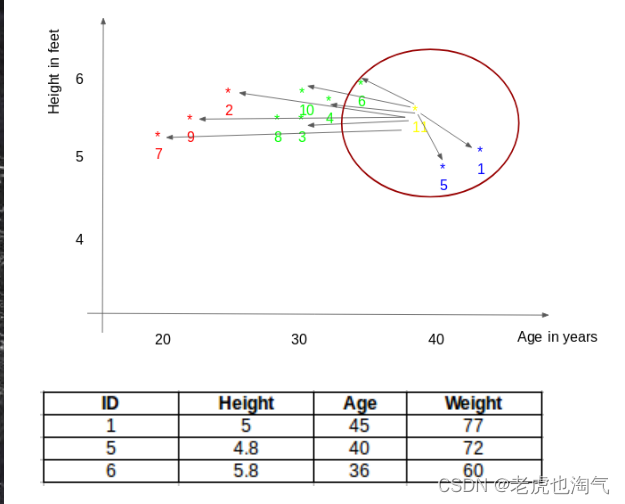
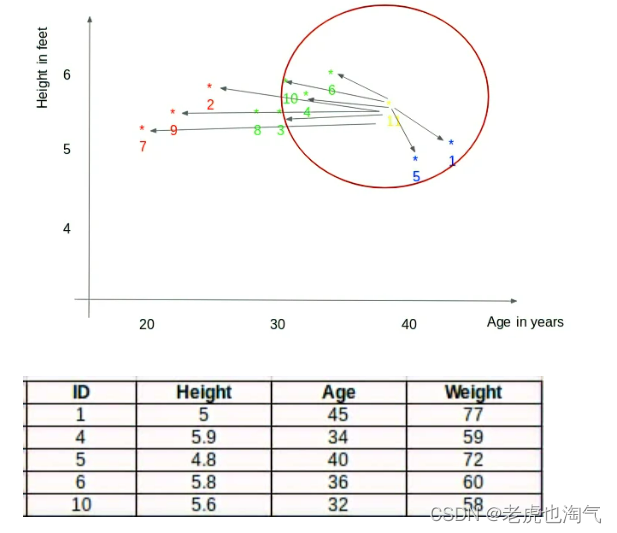
我们先看一个案例，这样可以更直观的理解KNN算法。数据如下表，其中包括10个人的身高、体重和年龄数据，然后预测第十一个人的体重。
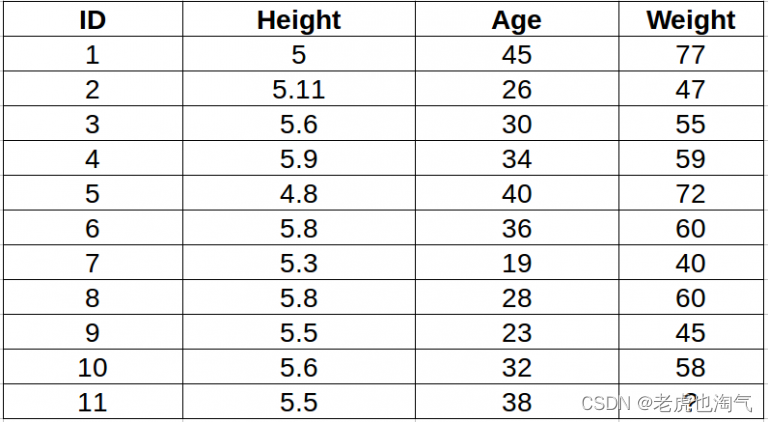
在这里插入图片描述
为了更清晰地了解数据间的关系，我们用坐标轴将身高和年龄表示出来，其中横坐标为年龄(a ge)、纵坐标为身高(Height)。
通过上图可以看到，11点的值是需要求解的，那么怎么求呢？我们可以看到在图中11点更接近于5点和1点，所以其体重应该更接近于5点和1点的值，也就是在72-77之间，这样我们就可以大致得到11点的体重值。下面我们用算法来实现这一过程。
KNN算法工作

如上所述，KNN可以用于分类和回归问题，通过样本间的某些相似特征来进行预测未知元素的值，即“物以类聚”：相同或相似的事物之间具有一些相似的特征。

在分类问题中，我们可以直接将其最近的样本值作为预测结果，那么在回归问题中怎么计算最终的预测结果呢？就像上面的例子，11点取值介于72-77之间，最终结果应该取多少合适呢？一般来说，我们将其平均值作为最终的预测结果。

1、计算待测点到已知点的距离
在这里插入图片描述
2、选择距离待测点最近的K个点，k值为人工设置的，至于k值如何设置合适在后边讨论。在这个例子中，我们假设 k=3，即点1、5、6被选择。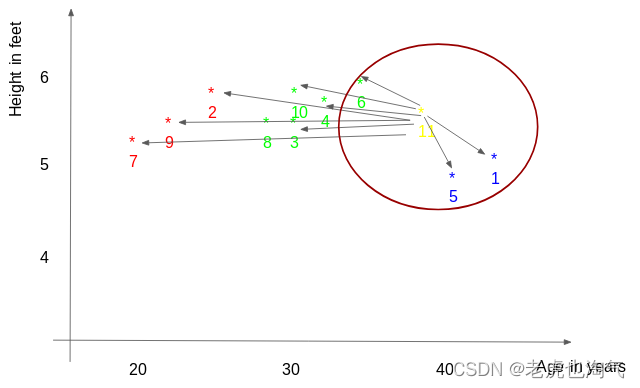
3、将点1、5、6的值取平均值作为最终的预测结果。即11点的Weight=(77+72+60)/3 = 69.66 kg
K值选择

K值代表最近邻的个数，k值的选择对预测结果有较大影响。

在上面的例子中，我们选择k=3时
在这里插入图片描述
最终的预测结果为

ID11 = (77+72+60)/3
ID11 = 69.66 kg

当我们选择k=5时
在这里插入图片描述
最终的预测结果为

ID 11 = (77+59+72+60+58)/5
ID 11 = 65.2 kg
我们可以看到k值不同结果也将不同，因此我们需要选择一个合适的k值来获得最佳的预测结果。我们的目标就是获得预测值与真实值之间最小的误差。

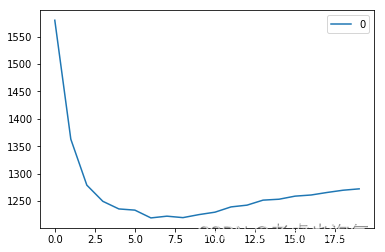
下面我们看一下k值与误差的关系曲线

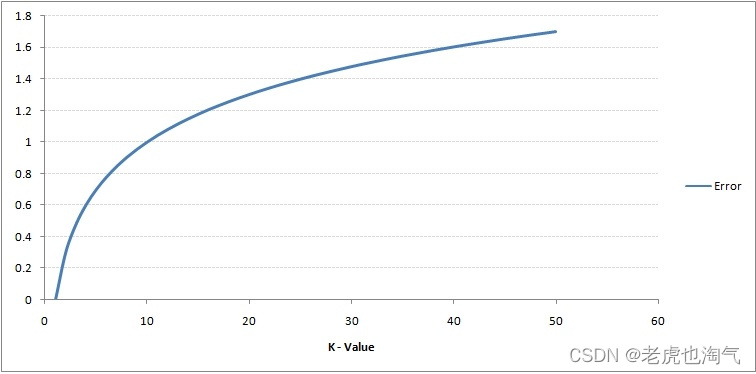
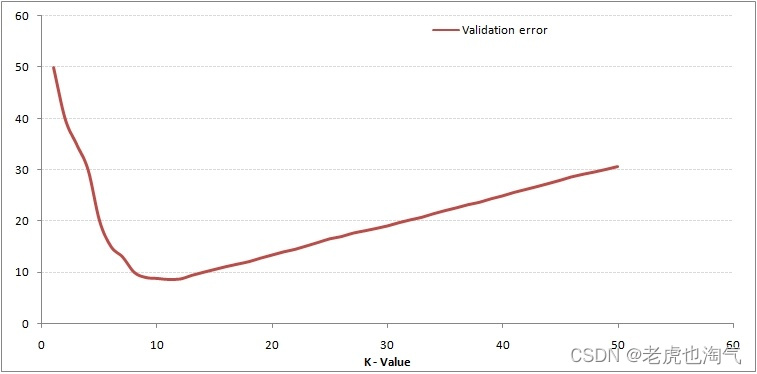
在这里插入图片描述

由曲线可得，如果K值太小，则会发生过拟合；如果k值太大，则会发生欠拟合。因此我们根据误差曲线选择最佳k值为9，你也可以使用其他方法寻找最佳k值。

python 实现 代码

1、读取数据

import pandas as pd
df = pd.read_csv('train.csv')
df.head()

2、处理缺失值

df.isnull().sum()
#missing values in Item_weight and Outlet_size needs to be imputed
mean = df['Item_Weight'].mean() #imputing item_weight with mean
df['Item_Weight'].fillna(mean, inplace =True)
 
mode = df['Outlet_Size'].mode() #imputing outlet size with mode
df['Outlet_Size'].fillna(mode[0], inplace =True)

3、处理分类变量并删除ID列

df.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1, inplace=True)
df = pd.get_dummies(df)

4、划分训练集与测试

df.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1, inplace=True)from sklearn.model_selection import train_test_split
train , test = train_test_split(df, test_size = 0.3)
 
x_train = train.drop('Item_Outlet_Sales', axis=1)
y_train = train['Item_Outlet_Sales']
 
x_test = test.drop('Item_Outlet_Sales', axis = 1)
y_test = test['Item_Outlet_Sales']
df = pd.get_dummies(df)

5、特征标准化

from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
 
x_train_scaled = scaler.fit_transform(x_train)
x_train = pd.DataFrame(x_train_scaled)
 
x_test_scaled = scaler.fit_transform(x_test)
x_test = pd.DataFrame(x_test_scaled)

6、查看误差曲线

from sklearn import neighbors
from sklearn.metrics import mean_squared_error 
from math import sqrt
import matplotlib.pyplot as plt
%matplotlib inline
rmse_val = [] #to store rmse values for different k
for K in range(20):
    K = K+1
    model = neighbors.KNeighborsRegressor(n_neighbors = K)
 
    model.fit(x_train, y_train)  #fit the model
    pred=model.predict(x_test) #make prediction on test set
    error = sqrt(mean_squared_error(y_test,pred)) #calculate rmse
    rmse_val.append(error) #store rmse values
    print('RMSE value for k= ' , K , 'is:', error)
curve = pd.DataFrame(rmse_val) #elbow curve 
curve.plot()

输出
在这里插入图片描述
由误差曲线可得我们选择k=7可以获得最优结果

预测结果

test = pd.read_csv('test.csv')
submission = pd.read_csv('SampleSubmission.csv')
submission['Item_Identifier'] = test['Item_Identifier']
submission['Outlet_Identifier'] = test['Outlet_Identifier']
 
#preprocessing test dataset
test.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1, inplace=True)
test['Item_Weight'].fillna(mean, inplace =True)
test = pd.get_dummies(test)
test_scaled = scaler.fit_transform(test)
test = pd.DataFrame(test_scaled)
 
#predicting on the test set and creating submission file
predict = model.predict(test)
submission['Item_Outlet_Sales'] = predict
submission.to_csv('submit_file.csv',index=False)