03、K-means聚类实现步骤与基于K-means聚类的图像压缩（2）

本文介绍: 对于一张RGB888的彩色图像，假设其大小为1920 * 1080，那么其存储所需的大小为1920*1080 * 24（因为RGB分别用8位来表示，因此每个像素点有24位来表示其颜色）。此处有24位来表示颜色，可表示的颜色个数为2^24种，假设此处使用K=16的K-m e ans 聚类算法对其进行压缩，则代表压缩后的图像只包含K种颜色。

03、K-means 聚类 实现 步骤与基于K-means聚类的图像压缩（2）

工程下载：K-means聚类实现步骤与基于K-means聚类的图像压缩

其他：
03、K-means聚类实现步骤与基于K-means聚类的图像压缩（1）
03、K-means聚类实现步骤与基于K-means聚类的图像压缩（2）

K-means聚类的图像压缩

开始学习机器学习啦，已经把吴恩达的课全部刷完了，现在开始熟悉一下复现代码。对这个手写数字实部比较感兴趣，作为入门的素材非常合适。

1、K-means聚类 图像压缩基本思路

我的想法是：这副图像存在许多很大一块区域的颜色相近，既然相近，我们就用一种颜色替代一大块区域中的各色。我们可以人为的用8、16、24、32种颜色表示整幅图像的颜色，也即说明聚类的个数为8、16、24、32。

上述说法是不准确的，准确的说法是：这副图像虽然很大，但是其有些部分颜色相近，这些颜色相近的部分不论是否出自同一位置，我们都可以用一种颜色进行替代。我们可以使用8、16、24、32种颜色来代替原来图中的所有颜色。

在使用K-means聚类进行图像压缩时，聚类的对象仅仅是颜色而已，和颜色的所在位置是否相近无关，也就是说这种压缩不改变像素的大小，只改变色彩的鲜艳程度而已。具体来讲，聚类是在三维坐标下进行的，三个坐标轴分别为R G B 的具体数值。

下面简单介绍这种压缩算法的压缩效果。对于一张RGB888的彩色图像，假设其大小为1920 * 1080，那么其存储所需的大小为1920*1080 * 24（因为RGB分别用8位来表示，因此每个像素点有24位来表示其颜色）。

此处有24位来表示颜色，可表示的颜色个数为2^24种，假设此处使用K=16的K-means聚类算法对其进行压缩，则代表压缩后的图像只包含K种颜色。

那么对于每个像素点而言，则需要 log2（K）=4位来进行表示，此外还需要K*24的空间来存储对应的24位RGB颜色，因此压缩后的总空间为1920 * 1080 * log2（K）+ K * 24。

对于一张1920 * 1080 的图像，压缩比例和K的对应关系如下所示：
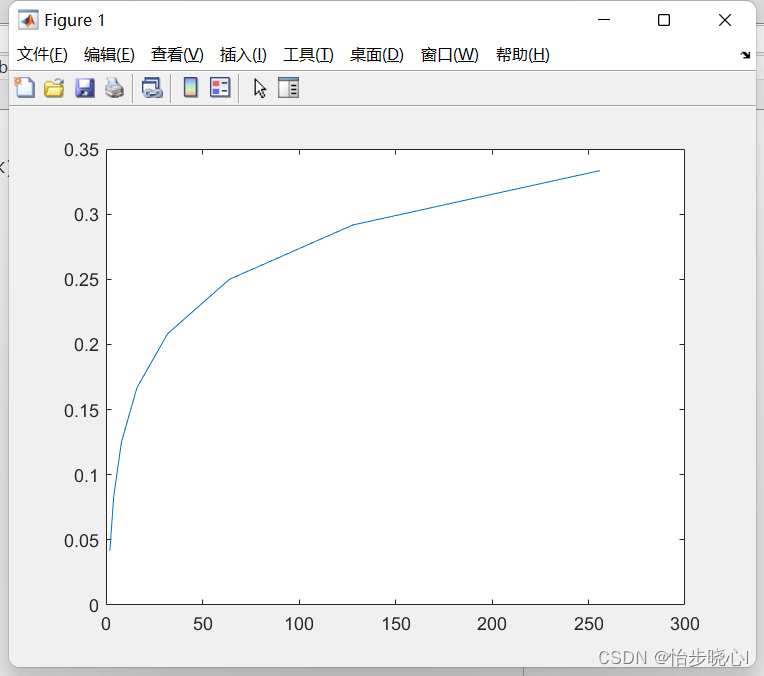
在这里插入图片描述

2、K-means聚类图像压缩底层 实现

此处从K-means聚类的底层原理进行实现，不调用库函数：

import numpy as np
from matplotlib import pyplot as plt


# 随机初始化聚类初始优化点
def kMeans_init_centroids(X, K):
    # 随机重新排序样本的索引
    randidx = np.random.permutation(X.shape[0])
    # 取前K个样本作为聚类中心
    centroids = X[randidx[:K]]
    return centroids


def find_closest_centroids(X, centroids):
    # 获取聚类中心的数量，也即K值
    K = centroids.shape[0]

    # 初始化一个数组用于存储每个样本所属的聚类中心的索引
    idx = np.zeros(X.shape[0], dtype=int)
    # 遍历数据集中的每个样本
    for i in range(X.shape[0]):
        # 初始化一个列表用于存储当前样本到每个聚类中心的距离
        distance = []
        # 计算当前样本到每个聚类中心的距离
        for j in range(centroids.shape[0]):
            # 使用欧几里得距离公式计算样本i与聚类中心j之间的距离
            norm_ij = np.linalg.norm(X[i] - centroids[j])
            distance.append(norm_ij)
            # 找出距离列表中的最小值，该最小值对应的索引就是当前样本所属的聚类中心
        idx[i] = np.argmin(distance)
        # 返回每个样本所属的聚类中心的索引数组
    return idx


def compute_centroids(X, idx, K):
    # 获取数据集X的行数m和列数n
    # m表示样本数量，n表示每个样本的特征数量
    m, n = X.shape
    # 初始化一个K x n的零矩阵，用于存储K个聚类中心
    # K表示聚类数量，n表示特征数量
    centroids = np.zeros((K, n))
    # 遍历每个聚类中心
    for k in range(K):
        # 从数据集X中选择属于当前聚类k的所有样本
        # idx是一个长度为m的数组，存储了每个样本所属的聚类中心的索引
        points = X[idx == k]
        # 计算属于当前聚类k的所有样本的平均值，得到聚类中心
        # axis=0表示按列计算平均值
        centroids[k] = np.mean(points, axis=0)
        # 返回计算得到的K个聚类中心
    return centroids


def run_kMeans(X, initial_centroids, max_iters=10):
    # 获取数据集X的行数m和列数n
    # m表示样本数量，n表示每个样本的特征数量
    m, n = X.shape
    # 获取初始聚类中心的数量K
    K = initial_centroids.shape[0]
    # 将初始聚类中心赋值给centroids变量
    centroids = initial_centroids
    # 将初始聚类中心复制给previous_centroids变量，用于后续比较聚类中心是否发生变化
    previous_centroids = centroids
    # 初始化一个长度为m的零数组，用于存储每个样本所属的聚类中心的索引
    idx = np.zeros(m)
    # 开始运行K-means算法，最多迭代max_iters次
    for i in range(max_iters):
        # 输出当前迭代进度
        print("K-Means iteration %d/%d" % (i, max_iters - 1))
        # 调用find_closest_centroids函数，为数据集X中的每个样本找到最近的聚类中心，并返回索引数组
        idx = find_closest_centroids(X, centroids)
        # 调用compute_centroids函数，根据每个样本所属的聚类中心和索引数组，计算新的聚类中心
        centroids = compute_centroids(X, idx, K)
        # 返回最终的聚类中心和每个样本所属的聚类中心的索引
    return centroids, idx

# Load an image of a bird
original_img = plt.imread('K_means_data/bird_small.png')
# Visualizing the image
plt.imshow(original_img)
plt.show()
print("Shape of original_img is:", original_img.shape)

# Divide by 255 so that all values are in the range 0 - 1
# RGB各8位，将其归一化至0-1
original_img = original_img / 255
# Reshape the image into an m x 3 matrix where m = number of pixels
# 数组的内容是图像各个点的颜色，m x 3
X_img = np.reshape(original_img, (original_img.shape[0] * original_img.shape[1], 3))

# K就是要使用几种颜色进行表达
K = 8
max_iters = 10

# Using the function you have implemented above. 初始化的是rgb的数值，因此是包含三个元素的数组
initial_centroids = kMeans_init_centroids(X_img, K)

# Run K-Means - this takes a couple of minutes
centroids, idx = run_kMeans(X_img, initial_centroids, max_iters)

# Represent image in terms of indices
X_recovered = centroids[idx, :]

# Reshape recovered image into proper dimensions
X_recovered = np.reshape(X_recovered, original_img.shape)

# Display original image
fig, ax = plt.subplots(1, 2, figsize=(8, 8))
plt.axis('off')

ax[0].imshow(original_img * 255)
ax[0].set_title('Original')
ax[0].set_axis_off()

# Display compressed image
ax[1].imshow(X_recovered * 255)
ax[1].set_title('Compressed with %d colours' % K)
ax[1].set_axis_off()
plt.show()

3、K-means聚类图像压缩库函数 实现

此处直接使用from sklearn.cluster import KMeans来进行K-means聚类，代码更加简洁了：

import matplotlib.pyplot as plt  # plt 用于显示图片
import matplotlib.image as mpimg  # mpimg 用于读取图片
from sklearn.cluster import KMeans
import numpy as np

original_pixel = mpimg.imread('K_means_data/bird_small.png')
pixel = original_pixel.reshape((128 * 128, 3))

kmeans = KMeans(n_clusters=8, random_state=0).fit(pixel)

newPixel = []
for i in kmeans.labels_:
    newPixel.append(list(kmeans.cluster_centers_[i, :]))

newPixel = np.array(newPixel)
newPixel = newPixel.reshape((128, 128, 3))


# Display original image
fig, ax = plt.subplots(1, 2, figsize=(8, 8))
plt.axis('off')
ax[0].imshow(original_pixel)
ax[0].set_title('Original')
ax[0].set_axis_off()

# Display compressed image
ax[1].imshow(newPixel)
ax[1].set_title('Compressed with %d colours' % kmeans.n_clusters)
ax[1].set_axis_off()
plt.show()