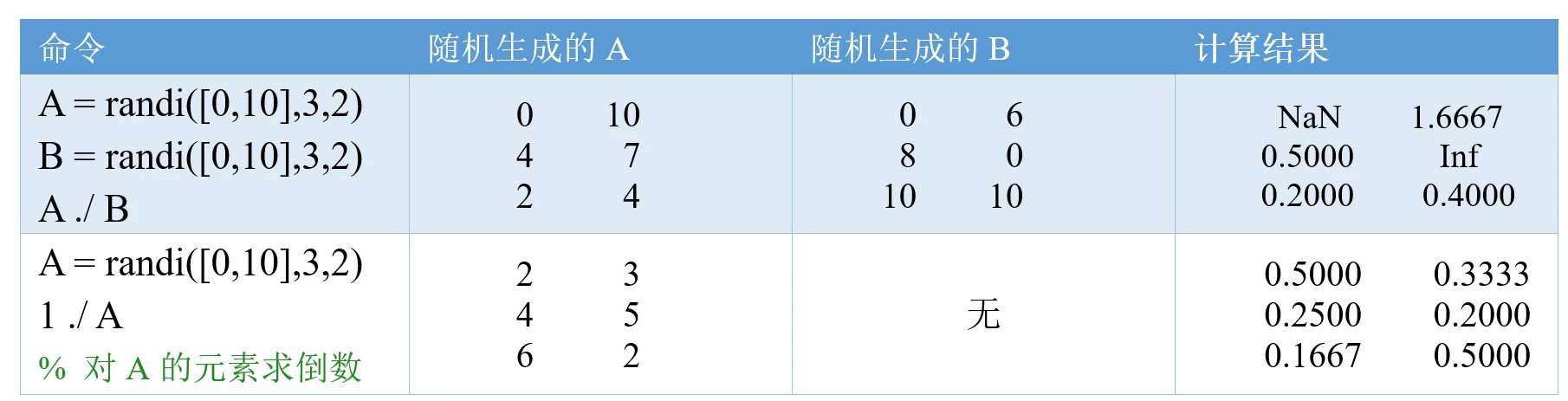
σ1−σ21∗21∗i=1∑m(yi−θ⊤xi)2
目标是让似然函数(对数变换之后)越大越好:
l
o
L
(
θ
)
→
i
n
J
(
θ
)
=
1
2
∑
i
=
1
(
y
i
−
θ
⊤
x
i
)
2
(最小二乘法)
max log L(theta)\ →min J(theta)=frac12 sum_{i=1}^m(y_i-theta^top x_i)^2(最小二乘法)
max logL(θ)→min J(θ)=21i=1∑m(yi−θ⊤xi)2(最小二乘法)
J
(
θ
)
=
1
2
∑
i
=
1
(
y
i
−
θ
⊤
x
i
)
2
J(theta)=frac12 sum_{i=1}^m(y_i-theta^top x_i)^2
J(θ)=21∑i=1m(yi−θ⊤xi)2即为最小二乘法。
J
(
θ
)
=
1
2
∑
i
=
1
m
(
y
i
−
θ
⊤
x
i
)
2
=
1
2
(
X
θ
−
y
)
⊤
(
X
θ
−
y
)
对
θ
求偏导
:
∇
θ
J
(
θ
)
=
X
⊤
X
θ
−
X
⊤
y
令
∇
θ
J
(
θ
)
=
0
得
:
θ
=
(
X
⊤
X
)
−
1
X
⊤
y
J(theta)=frac12 sum_{i=1}^m(y_i-theta^top x_i)^2= frac12(Xtheta-y)^top (Xtheta-y)\ 对theta 求偏导:\ nabla_theta J(theta)=X^top Xtheta-X^top y\ 令nabla_theta J(theta)=0得:\ theta=(X^top X)^{-1}X^top y
J(θ)=21i=1∑m(yi−θ⊤xi)2=21(Xθ−y)⊤(Xθ−y)对θ求偏导:∇θJ(θ)=X⊤Xθ−X⊤y令∇θJ(θ)=0得:θ=(X⊤X)−1X⊤y
采用微分和迹的关系
f
=
t
(
(
∂
f
∂
X
)
⊤
X
)
df= tr((frac{partial f}{partial X})^top dX)
J
(
θ
)
=
t
(
J
(
θ
)
)
=
[
1
2
(
X
θ
−
y
)
⊤
(
X
θ
−
y
)
]
=
t
[
(
1
2
(
θ
⊤
X
⊤
X
θ
−
2
y
⊤
X
θ
+
y
⊤
y
)
)
]
=
t
[
(
1
2
θ
⊤
X
⊤
X
θ
)
]
−
t
r
(
d
(
2
y
⊤
X
θ
)
)
+
t
r
(
d
(
y
⊤
y
)
)
=
t
r
(
1
2
d
θ
⊤
X
⊤
X
θ
)
+
t
r
(
1
2
θ
⊤
X
⊤
X
d
θ
)
−
t
r
(
2
y
⊤
X
d
θ
)
+
0
=
t
r
(
1
2
θ
⊤
X
⊤
X
d
θ
)
+
t
r
(
1
2
θ
⊤
X
⊤
X
d
θ
)
−
t
r
(
2
y
⊤
X
d
θ
)
=
t
r
(
θ
⊤
X
⊤
X
d
θ
−
2
y
⊤
X
d
θ
)
=
t
r
(
(
θ
⊤
X
⊤
X
−
2
y
⊤
X
)
d
θ
)
=
t
r
(
(
X
⊤
X
θ
−
2
X
⊤
y
)
⊤
d
θ
)
故:
∂
J
(
θ
)
∂
θ
=
X
⊤
X
θ
−
2
X
⊤
y
dJ(theta)= tr(dJ(theta))=d[frac12(Xtheta-y)^top (Xtheta-y)]\ =tr[d(frac12(theta^top X^top Xtheta-2y^top Xtheta+y^top y))]\ =tr[d(frac12theta^top X^top Xtheta)]-tr(d(2y^top Xtheta))+tr(d(y^top y))\ =tr(frac12dtheta^top X^top Xtheta)+tr(frac12theta^top X^top Xdtheta)-tr(2y^top Xdtheta)+0\ =tr(frac12theta^top X^top Xdtheta)+tr(frac12theta^top X^top Xdtheta)-tr(2y^top Xdtheta)\ =tr(theta^top X^top Xdtheta-2y^top Xdtheta)=tr((theta^top X^top X-2y^top X)dtheta)\ =tr(( X^top Xtheta – 2X^top y)^top dtheta)\ 故:\ frac{partial J(theta)}{partial theta}=X^top Xtheta – 2X^top y\
dJ(θ)=tr(dJ(θ))=d[21(Xθ−y)⊤(Xθ−y)]=tr[d(21(θ⊤X⊤Xθ−2y⊤Xθ+y⊤y))]=tr[d(21θ⊤X⊤Xθ)]−tr(d(2y⊤Xθ))+tr(d(y⊤y))=tr(21dθ⊤X⊤Xθ)+tr(21θ⊤X⊤Xdθ)−tr(2y⊤Xdθ)+0=tr(21θ⊤X⊤Xdθ)+tr(21θ⊤X⊤Xdθ)−tr(2y⊤Xdθ)=tr(θ⊤X⊤Xdθ−2y⊤Xdθ)=tr((θ⊤X⊤X−2y⊤X)dθ)=tr((X⊤Xθ−2X⊤y)⊤dθ)故:∂θ∂J(θ)=X⊤Xθ−2X⊤y
当
X
⊤
X
X^top X
∂
J
(
θ
)
∂
θ
=
X
⊤
X
θ
−
2
X
⊤
y
=
0
frac{partial J(theta)}{partial theta}=X^top Xtheta – 2X^top y=0
∂θ∂J(θ)=X⊤Xθ−2X⊤y=0得到:
θ
=
(
X
⊤
X
)
−
1
X
⊤
y
theta=(X^top X)^{-1}X^top y
θ=(X⊤X)−1X⊤y
其中
(
X
⊤
X
)
−
1
(X^top X)^{-1}
(X⊤X)−1是矩阵
X
⊤
X
X^top X
X⊤X的逆矩阵。但是现实任务中,
X
⊤
X
X^top X
X⊤X通常不是满秩矩阵,例如在许多任务中会遇到大量的变量,其数目甚至超过样例数,导致X的列数多于行数,
X
⊤
X
X^top X
X⊤X ,
X
⊤
X
X^top X
θ
theta
θ,他们都能使均方差最小化。选择哪一个解作为输出,将由机器学习算法的归纳偏好决定,常见的做法是引入正则化项。
原文地址:https://blog.csdn.net/Gaowang_1/article/details/134577250
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_14635.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!