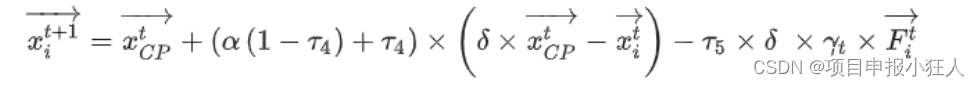基于DCT变换的图像压缩解压缩算法matlab仿真

本文介绍: 基于DCT（离散余弦变换）的图像压缩与解压缩算法。我们深入探讨了DCT变换的原理、其在图像编码中的应用，并给出了相应的数学公式和算法实现细节。随着数字技术的快速发展，图像数据在日常生活中呈现爆炸性增长。因此，如何有效地压缩图像数据，同时确保良好的图像质量，成为了一个重要的研究课题。DCT变换由于其良好的能量集中特性和与人类视觉系统的匹配度，被广泛应用于图像压缩标准中，如JPEG。

1.算法运行效果图预览

1.算法运行 效果图 预览

2.算法运行 软件 版本

MATLAB2022a

3.部分核心 程序

....................................................................
%调用8x8矩阵的量化等级  
load Q10.mat

% 对R、G、B通道应用压缩函数func_ys，得到压缩后的图像Rys、Gys、Bys  
Rys  = func_ys(R1,Coff_dct,Q_dct,Bsize);
Gys  = func_ys(G1,Coff_dct,Q_dct,Bsize);
Bys  = func_ys(B1,Coff_dct,Q_dct,Bsize);

% 将压缩后的通道数据合并成一个新的图像I1ys  
I1ys(:,:,1) = Rys;
I1ys(:,:,2) = Gys;
I1ys(:,:,3) = Bys;
imwrite(I1ys,'TMPSIys.jpg');% 将图像I1ys写入到文件'TMPSIys.jpg'中  

% 对压缩后的图像应用解压缩函数func_deys，得到解压缩后的图像Rdeys、Gdeys、Bdeys  
Rdeys        = func_deys(Rys,Coff_dct,Q_dct,Bsize);
Gdeys        = func_deys(Gys,Coff_dct,Q_dct,Bsize);
Bdeys        = func_deys(Bys,Coff_dct,Q_dct,Bsize);
% 将解压缩后的通道数据合并成一个新的图像I2deys，并转换为uint8类型  
I2deys(:,:,1) = uint8(Rdeys);
I2deys(:,:,2) = uint8(Gdeys);
I2deys(:,:,3) = uint8(Bdeys);
imwrite(I2deys,'TMPSIdeys.jpg');% 将图像I2deys写入到文件'TMPSIdeys.jpg'中  



% 获取原始图像文件和压缩后的图像文件的大小（字节） 

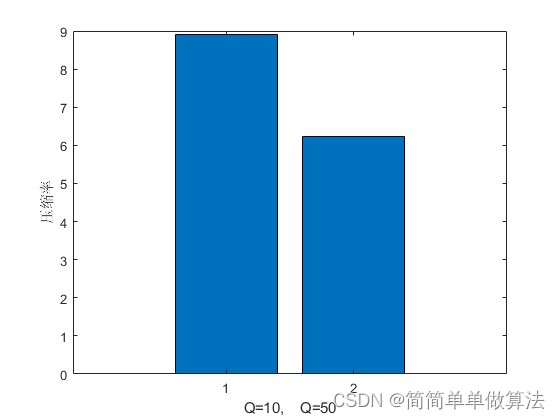
%压缩率
ys_rate = SIZE1/SIZE2;

% 显示三个图像：压缩后的图像、解压后的图像、原始图像  
figure(1)
subplot(131)
imshow(I1ys);
title('压缩图像')
subplot(132)
imshow(I2deys);
title('解压图像')
subplot(133)
imshow(I0);
title('原始图像')


I00 = imread('TMPSIdeys.jpg');
err = (double(I0) - double(I00)) .^ 2;
mse1= sum(err(:)) / (64*64); 
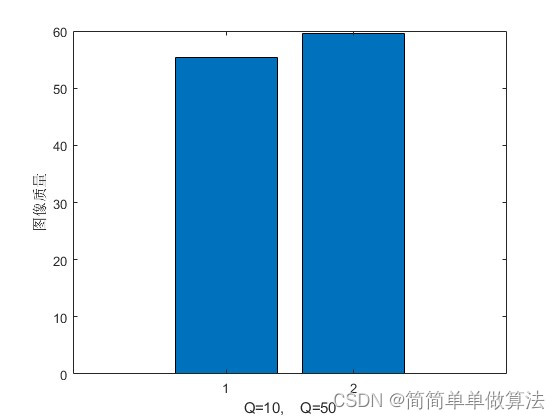
%PSNR 
Max_pixel = 255;
PSNR      = 20*log10((Max_pixel^2)./sqrt(mse1));
 

save R1.mat ys_rate PSNR
00084

4.算法理论概述

基于DCT（离散余弦变换）的图像压缩与解压缩算法。我们深入探讨了DCT变换的原理、其在图像编码中的应用，并给出了相应的数学公式和算法实现细节。随着数字技术的快速发展，图像数据在日常生活中呈现爆炸性增长。因此，如何有效地压缩图像数据，同时确保良好的图像质量，成为了一个重要的研究课题。DCT变换由于其良好的能量集中特性和与人类视觉系统的匹配度，被广泛应用于图像压缩标准中，如JPEG。

4.1、DCT变换原理

离散余弦变换（DCT）是傅里叶变换的一种变种。它将信号从时域变换到频域，使得信号的能量大部分集中在几个频率分量上。对于图像而言，DCT可以有效地将图像的能量集中在左上角的低频部分。

一维DCT变换公式如下：

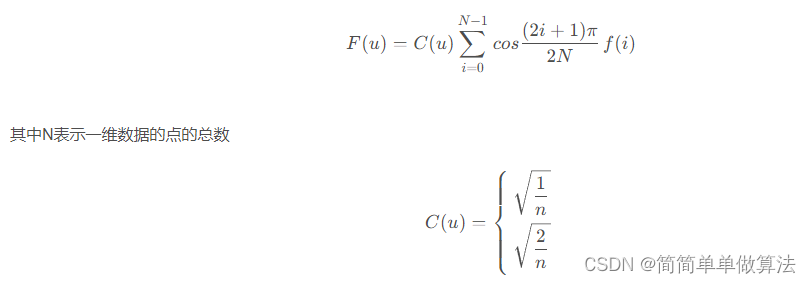
二维DCT变换（通常用于图像处理）可以通过两次一维DCT变换实现，首先对行进行变换，再对列进行变换。

可以发现，二维DCT变换其实是在一维DCT变换的基础上，再做一次一维DCT变换。二维DCT也可以写成矩阵相乘的形式：

二维DCT变换的复杂度达到O(n^4)，所以进行DCT变换的矩阵不宜过大。在实际处理图片的过程中，需要先把矩阵分块，一般分为8×8或16×16大小，这样DCT变换不至于耗费过多的时间。

4.2、基于DCT的图像压缩

基于DCT的图像压缩主要步骤如下：

分块：将原始图像分为8×8或16×16的小块。
DCT变换：对每个小块进行二维DCT变换。
量化：使用预定的量化表对DCT系数进行量化，这一步骤是有损的，会丢失部分信息。
编码：采用Zig-Zag 扫描将量化后的系数排列为一维序列，并使用霍夫曼编码进行进一步压缩。
通过以上的步骤，我们可以实现图像的压缩。需要注意的是，量化步骤是有损的，因此解压后的图像与原始图像会存在一定的差异。