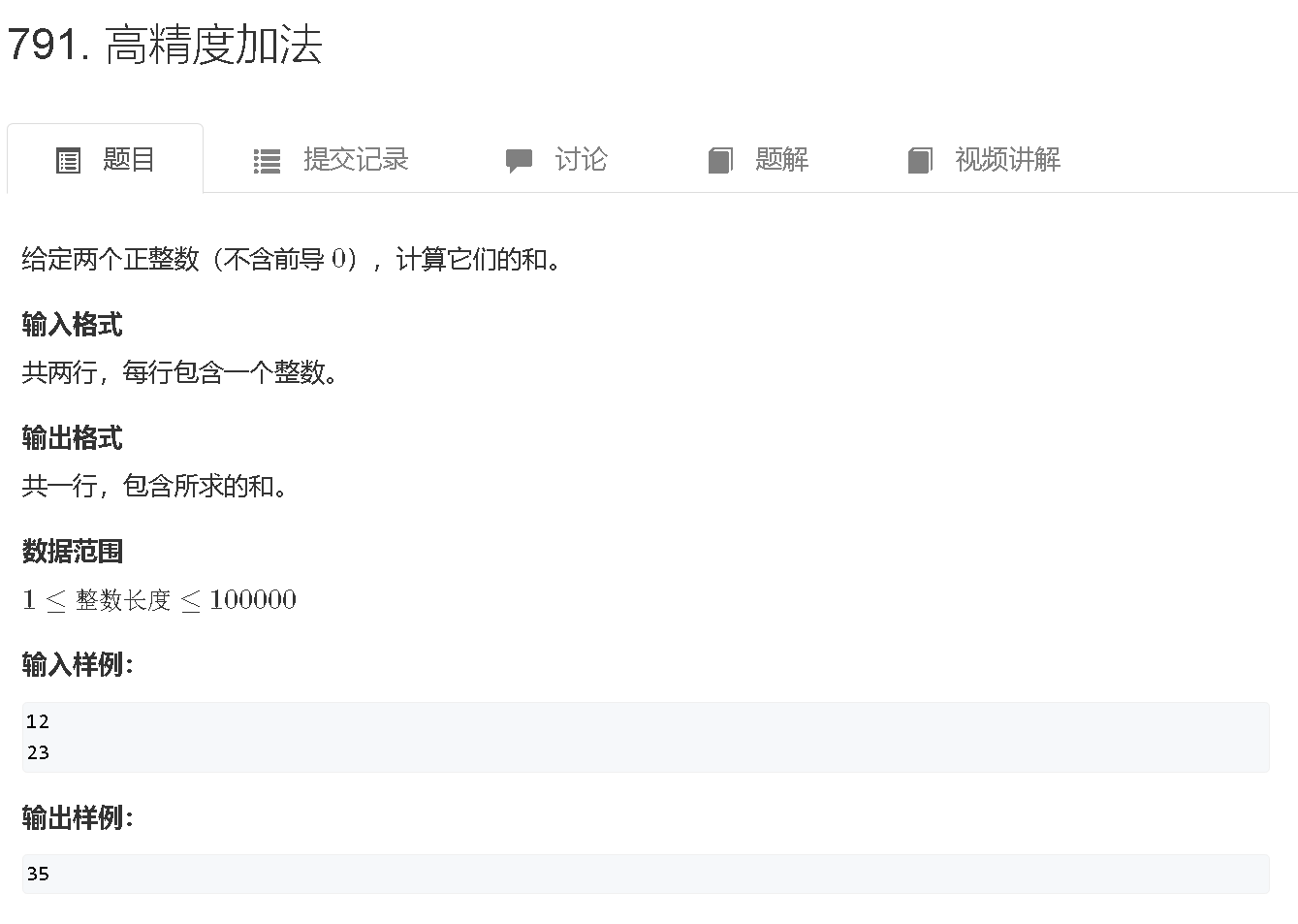
Long long ago, there lived two rabbits Tom and Jerry in the forest. On a sunny afternoon, they planned to play a game with some stones. There were n stones on the ground and they were arranged as a clockwise ring. That is to say, the first stone was adjacent to the second stone and the n-th stone, and the second stone is adjacent to the first stone and the third stone, and so on. The weight of the i-th stone is ai.
The rabbits jumped from one stone to another. Tom always jumped clockwise, and Jerry always jumped anticlockwise.
At the beginning, the rabbits both choose a stone and stand on it. Then at each turn, Tom should choose a stone which have not been stepped by itself and then jumped to it, and Jerry should do the same thing as Tom, but the jumping direction is anti-clockwise.
For some unknown reason, at any time , the weight of the two stones on which the two rabbits stood should be equal. Besides, any rabbit couldn’t jump over a stone which have been stepped by itself. In other words, if the Tom had stood on the second stone, it cannot jump from the first stone to the third stone or from the n-the stone to the 4-th stone.
Please note that during the whole process, it was OK for the two rabbits to stand on a same stone at the same time.
Now they want to find out the maximum turns they can play if they follow the optimal strategy.
Input
The input contains at most 20 test cases.
For each test cases, the first line contains a integer n denoting the number of stones.
The next line contains n integers separated by space, and the i-th integer ai denotes the weight of the i-th stone.(1 <= n <= 1000, 1 <= ai <= 1000)
The input ends with n = 0.
Output
For each test case, print a integer denoting the maximum turns.
1
1
4
1 1 2 1
6
2 1 1 2 1 3 0
1
4
5
Hint
For the second case, the path of the Tom is 1, 2, 3, 4, and the path of Jerry is 1, 4, 3, 2.
For the third case, the path of Tom is 1,2,3,4,5 and the path of Jerry is 4,3,2,1,5.
解析 :
性质:想要满足题目的意思,两只兔子只能在所给序列的最长回文子串上行走
子集划分:f[i][j]:表示区间 i 到 j 内的最长回文子串的长度是多少
状态转移 :
当 a[i]==a[j]: f[i][j]=f[i+1][j-1]+2;
否则:f[i][j]=max(f[i][j-1],f[i+1][j]);
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
using namespace std;
typedef long long LL;
const int N = 1e3 + 5;
int n,a[N];
int f[N][N];
int main() {
while (cin >> n,n) {
memset(f, 0, sizeof f);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
for (int i = 1; i <= n; i++) {
f[i][i] = 1;
}
for (int len = 2; len <= n; len++) {
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
if (a[i] == a[j]) {
f[i][j] = f[i + 1][j - 1] + 2;
}
else {
f[i][j] = max(f[i + 1][j], f[i][j - 1]);
}
}
}
int ans = 0;
for (int i = 1; i <= n; i++) {
ans = max(ans, f[1][i]+ f[i + 1][n]);
}
cout << ans << endl;
}
return 0;
}
原文地址:https://blog.csdn.net/Landing_on_Mars/article/details/134614226
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_19503.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!