数据结构与算法复习笔记

6.查找 算法

查找：
设记录表L=(R1 R2……Rn)，其中Ri(l≤i≤n)为记录，对给定的某个值k，在表L中确定key=k的记录的过程，称为查找。
若表L中存在一个记录Ri的key=k，记为Ri.key=k，则查找成功，返回该记录在表L中的序号i(或Ri 的地址)，否则(查找失败)返回0(或空地址Null)。

6.1.平均查找长度

对查找算法，主要分析其T(n)。查找过程是key的比较过程，时间主要耗费在各记录的key与给定k值的比较上。比较次数越多，算法效率越差（即T(n)量级越高），故用“比较次数”刻画算法的T(n)。

一般以“平均查找长度”来衡量T(n)。
平均查找长度ASL（Av e rag e Se arc h Leng t h）：对给定k，查找表L中记录比较次数的期望值(或平均值)，即：
在这里插入图片描述
Pi为查找Ri的概率。等概率情况下Pi=1/n；Ci为查找Ri时key的比较次数(或查找次数)。

6.2.顺序表的查找

顺序表，是将表中记录(R1 R2……Rn)按其序号存储于一维数组空间
 记录Ri的类型描述如下：

typedef struct
{ 
 keytype key;    //记录key//
	     ……   //记录其他项//
} Retype;

顺序表类型描述如下:

#define maxn 1024     //表最大长度//
typedef struct 
{   
	Retype data[maxn];  //顺序表空间//
 	int len;   //当前表长，表空时len=0//
} sqlist;

若说明：sqli s t r，则（r.data[1]，……，r.data[r.len]）为记录表(R1……Rn)， Ri.key为r.d a ta[i].key, r.data[0]称为监视哨，为算法设计方便所设。

算法思路: 设给定值为k，在表(R1 R2……Rn)中，从Rn开始，查找key=k的记录。

int sqsearch(sqlist r, keytype k)  
{   
	int i;
    r.data[0].key = k;  //k存入监视哨//
	i = r.len;  //取表长//
	while(r.data[i].key != k) i--;  
	return (i);
}

设Ci(1≤i≤n)为查找第i记录的key比较次数(或查找次数)：

		若r.data[n].key = k，       Cn=1；
		若r.data[n-1].key = k，     Cn-1=2；
       		    ……
		若r.data[i].key = k，        Ci=n-i+1；
       		    ……
		若r.data[1].key = k，        C1=n

故ASL = O(n)。而查找失败时，查找次数等于n+l，同样为O(n)。

对查找算法，若ASL=O(n)，则效率是很低的，意味着查找某记录几乎要扫描整个表，当表长n很大时，会令人无法忍受。

6.3.折半查找算法

算法思路:
对给定值k，逐步确定待查记录所在区间，每次将搜索空间减少一半(折半)，直到查找成功或失败为止。
设两个游标 low、hig h，分别指向当前待查找表的上界(表头)和下界(表尾)。mid 指向中间元素。
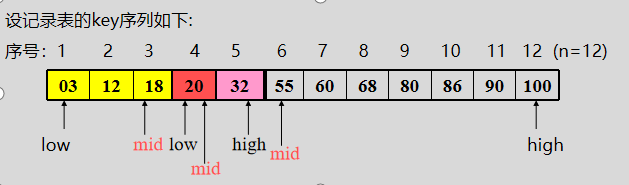
在这里插入图片描述
现查找k=20的记录。
再看查找失败的情况，设要查找k=85的记录。

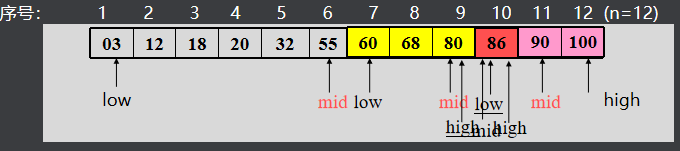
C语言实现如下：

int Binsearch(sqlist r, keytype k)    //对有序表r折半查找的算法//
{  
	int low, high, mid;  low = 1;high = r.len; 
	while (low <= high)    
	{  
		mid = (low+high) / 2;   
        if (k == r.data[mid].key)  
        	return (mid);  
        if (k < r.data[mid].key) 
        	high = mid-1;  
        else 
        	low = mid+1;
	}      
     return(0);
 }

不失一般性，设表长n=2h-l，h=log2(n+1)。记录数n恰为一棵h层的满二叉树的结点数。得出表的判定树及各记录的查找次数如图所示。
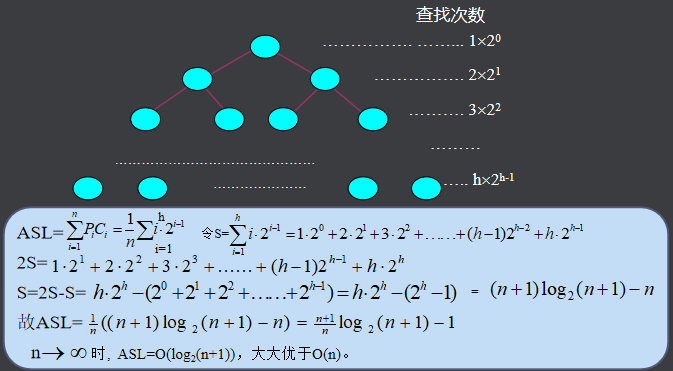
在这里插入图片描述

6.4.分块查找算法

设记录表长为n，将表的n个记录分成b=[n/s]个块，每块s个记录（最后一块记录数可以少于s个），即：
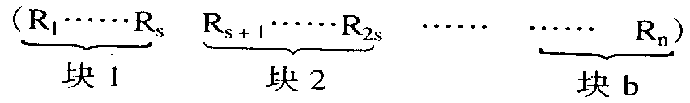
在这里插入图片描述
且表分块有序，即第i（1≤i≤b-1）块所有记录的key小于第i+1块中记录的key，但块内记录可以无序。
步骤：

建立索引
每块对应一索引项：
其中kmax为该块内记录的最大key；link为该块第一记录的序号（或指针）。
顺序、折半、分块查找和树表的查找中，其ASL的量级在O(n)～O(log2n)之间。
不论ASL在哪个量级，都与记录长度n有关。随着n的扩大，算法的效率会越来越低。
ASL与n有关是因为记录在存储器中的存放是随机的，或者说记录的key与记录的存放地址无关，因而查找只能建立在key的“比较”基础上。

7.排序算法

稳定排序和非稳定排序
设文件f=（R1……Ri……Rj……Rn）中记录Ri、Rj（i≠j，i、j=1……n）的key相等，即Ki=Kj。
若在排序前Ri领先于Rj，排序后Ri仍领先于Rj，则称这种排序是稳定的，其含义是它没有破坏原本已有序的次序。
内排序和外排序

若待排文件f在计算机的内存储器中，且排序过程也在内存中进行，称这种排序为内排序。
若排序中的文件存入外存储器，排序过程借助于内外存数据交换（或归并）来完成，则称这种排序为外排序。
各种内排序方法可归纳为以下五类：
（1）插入排序
（2）交换排序
（3）选择排序
（4）归并排序
插入排序方法可归纳为以下五类：
(1) 直接插入排序
(2) 折半插入排序
(3) 链表插入排序
(4) Shell（希尔）排序

设待排文件f=（R1 R2……Rn）相应的key集合为k={k1 k2……kn}，
排序方法:
先将文件中的（R1）看成只含一个记录的有序子文件，然后从R2起，逐个将R2至Rn按key插入到当前有序子文件中，最后得到一个有序的文件。插入的过程上是一个key的比较过程，即每插入一个记录时，将其key与当前有序子表中的key进行比较，找到待插入记录的位置后，将其插入即可。
设文件记录的key集合k={50，36，66，76，95，12，25，36}
在这里插入图片描述