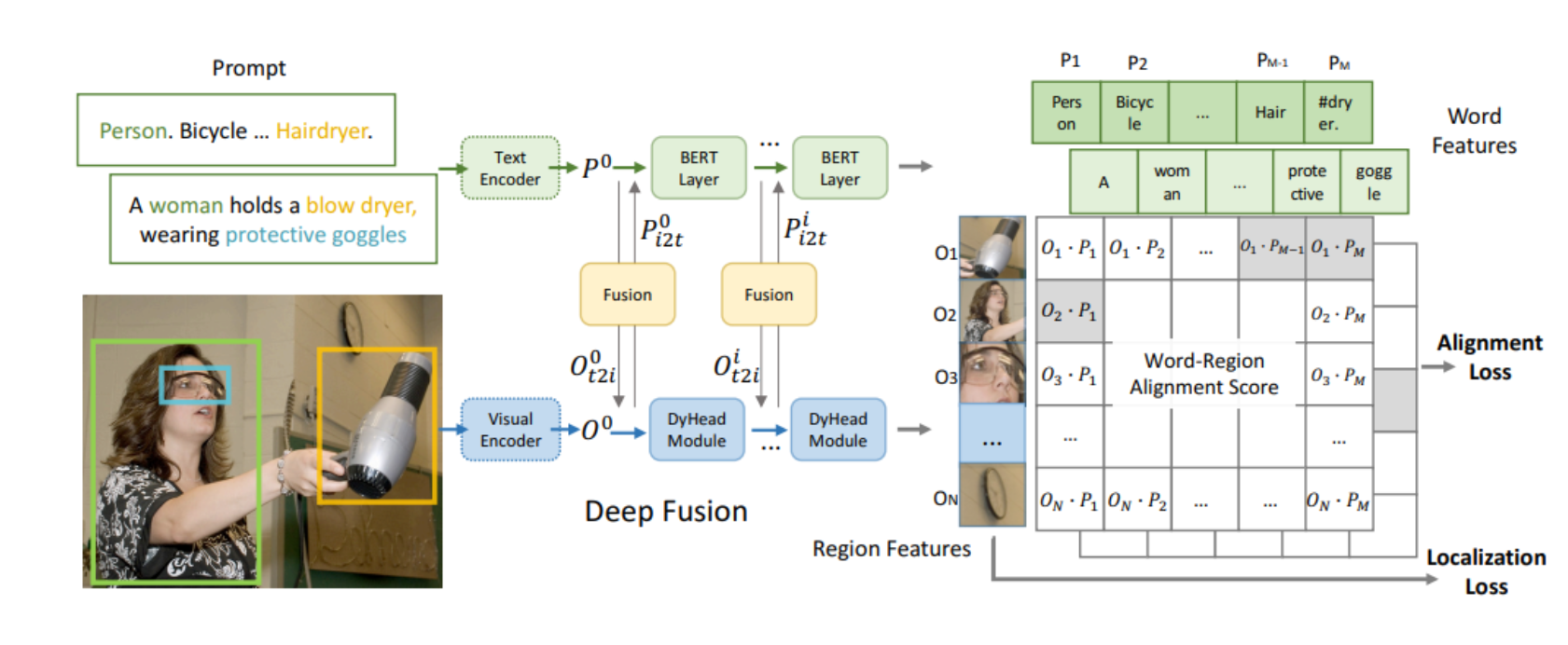
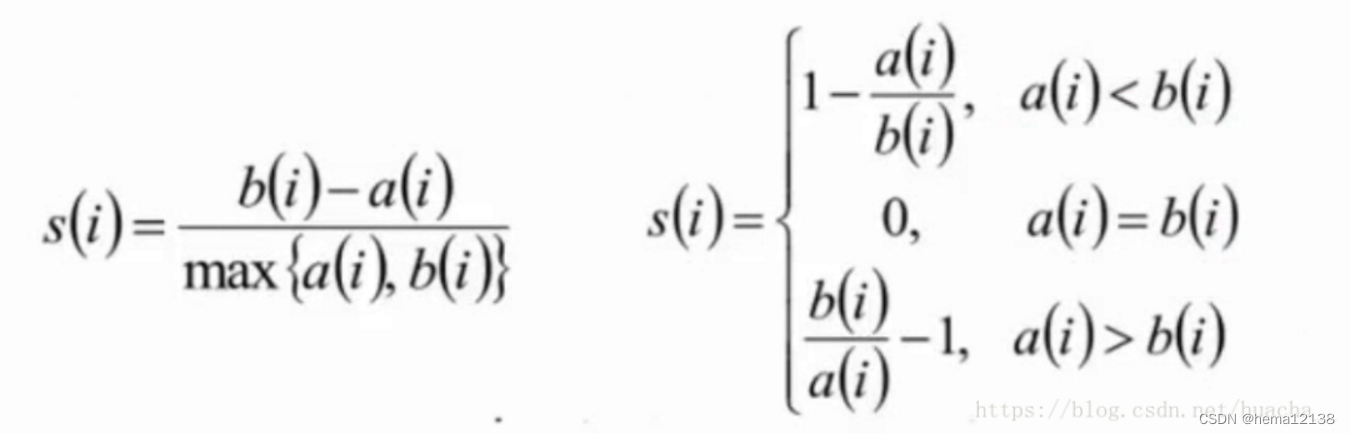本文介绍: 本文是对On the Identifiability of Nonlinear ICA: Sparsity and Beyond (NIPS 2022)中两个结构稀疏假设的总结。原文链接在Reference中。独立成分分析简单来说,就是给定很多的样本X,通过样本分离出组合成样本的源S。关于ICA的详细内容,可以参考Yifan Shen的博客:ICA简明攻略非线性独立成分分析(ICA)旨在从其可观测的非线性混合物中恢复潜在的独立源。非线性独立成分分析(ICA)是无监督学习的基础。它推广了线性ICA(Comon
0,(7)
根据(1),
U
^
hat{U}
U^应该是最小值,而(7)说明当
U
^
≠
D
P
hat{U} neq DP
U^=DP时,
U
^
hat{U}
U^ 不是最小值。与定义相违背。因此证明
U
^
=
D
P
hat{U} = DP
U^=DP,也就是
A
^
=
A
D
P
hat{A} = ADP
A^=ADP成立。
Reference
- Zheng, Yujia, Ignavier Ng, and Kun Zhang. “On the identifiability of nonlinear ica: Sparsity and beyond.” Advances in Neural Information Processing Systems 35 (2022): 16411-16422.
原文地址:https://blog.csdn.net/qq_43426078/article/details/134566566
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_2031.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。