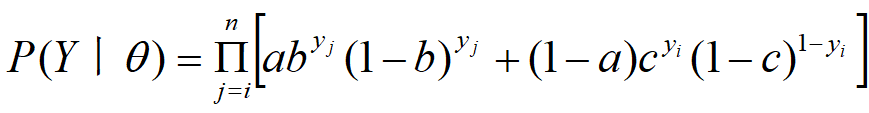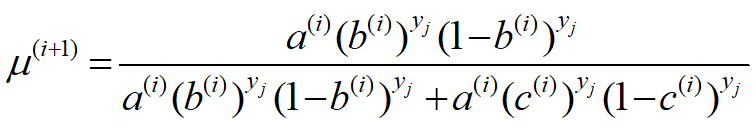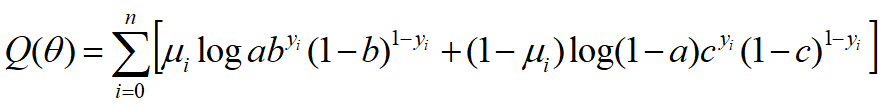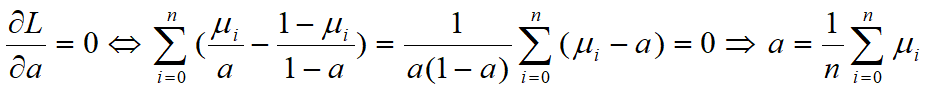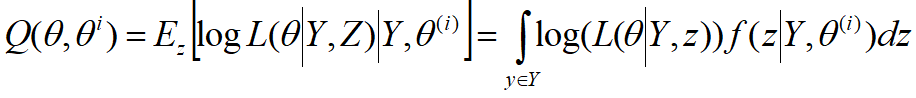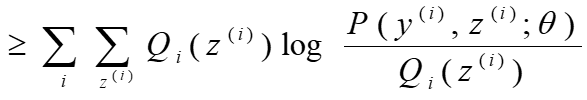本文介绍: EM算法是一种迭代算法,1977年由Dempster等人总结提出,用于含有隐变量的概率模型参。θ=θ(0)是使L(θ)取很大值,而θ中的其他θ的值使 L(θ)取值很小,自然认为取θ(0)作为未知参数。极大似然估计存在着问题是:①对于许多具体问题不能构造似然函数解析表达式 ②似然函数。极大似然估计是一种常用的参数估计方法,它是以观测值出现的概率最大作为准则。要用于非完全数据参数估计,它是通过假设隐变量的存在,极大化地简化了似然函数方程,从而解。数的极大似然估计,或极大后验概率估计。θ 的估计值较为合理。
1. 极大似然估计与EM算法
极大似然估计是一种常用的参数估计方法,它是以观测值出现的概率最大作为准则。关于极
大似然估计,假设现在已经取到样本值![]() 了,这表明取到这一样本的概率L(θ) 比较
了,这表明取到这一样本的概率L(θ) 比较
大。我们自然不会考虑那些不能使样本![]() 出现的θ作为估计值,再者,如果已知当
出现的θ作为估计值,再者,如果已知当
θ=θ(0)是使L(θ)取很大值,而θ中的其他θ的值使 L(θ)取值很小,自然认为取θ(0)作为未知参数
θ 的估计值较为合理。
在极大似然估计中,独立同分布(IID)的数据![]() , 其概率密度函数为
, 其概率密度函数为![]()
2. 3硬币模型
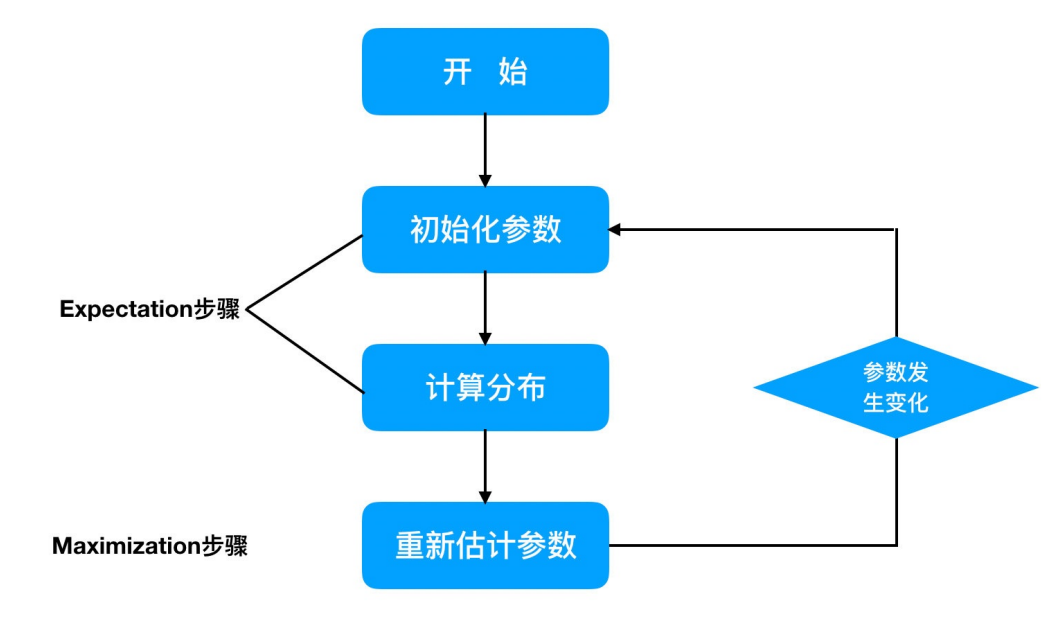
3. EM算法步骤
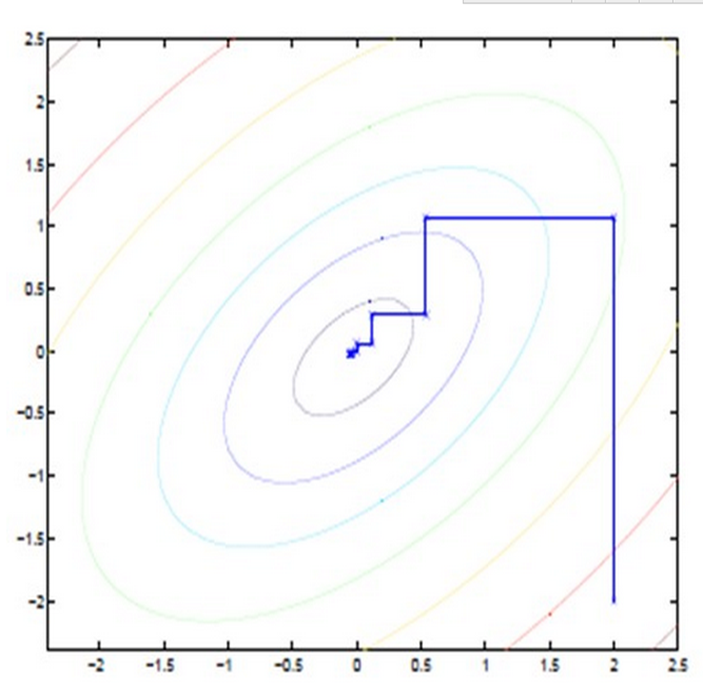
4. EM算法原理
5. EM算法补充
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。