当前位置：
  1. 首页
  2. 互联网
  3. 正文
本文介绍: 对线性代数的矩阵的运算有详细的总结，来源于B站宋浩的视频所作的学习笔记。


目录：


 一、矩阵的基本概念


 1、行矩阵与列矩阵


2、零矩阵


3、负矩阵


 4、方阵


 1）、方阵的定义


 2）、主对角线和次对角线


5、单位阵


 6、只有一个数字的矩阵


7、同型矩阵


 三、矩阵的运算


 1、加法、减法


2、数乘运算


 四、矩阵乘法


1、矩阵的乘法


2、矩阵乘法不满足的三条规律


 3、矩阵乘法的运算规律 


 4、矩阵的可交换


五、矩阵的幂运算


 六、简单的矩阵运算，学到的知识点运用起来。




一、矩阵的基本概念


矩阵本质上是一个数表，用_{}A_{m*n}表示，代表一个m*n的矩阵，有m行n列。


矩阵的运用场景非常多，例如关系的表示等。


如下图就是一个4行4列的矩阵。




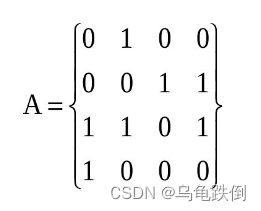
1、行矩阵与列矩阵


只有1行的矩阵叫做行矩阵




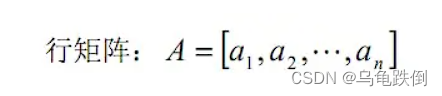
只有1列的矩阵叫做列矩阵




2、零矩阵


矩阵内的所有元素都是0，记作O




3、负矩阵


把原来矩阵的所有元素都取负号，为相反数，称为负矩阵。


例如A的负矩阵为-A。




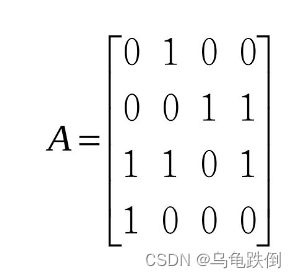
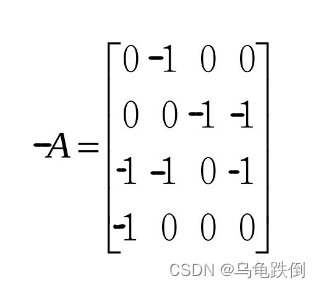
4、方阵


1）方阵的定义


行数等于列数的矩阵称为方阵，一般也称为n阶矩阵，即A_{n*n}，亦A_{n}


例如下面这个矩阵，就是三行三列的矩阵。




2）、主对角线和次对角线


只有在方阵中才有对角线的概念。如图：




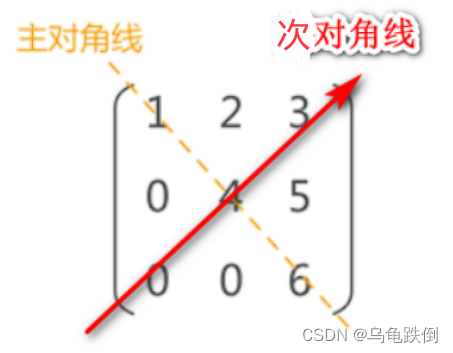
5、单位阵


对角线为1，其余元素为0，这种矩阵称为单位矩阵。记作E。




6、只有一个数字的矩阵


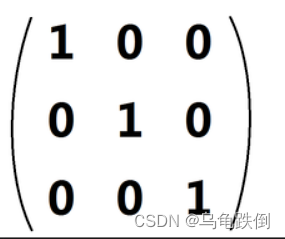
只有一个数字的矩阵也是矩阵。


例如：[5]






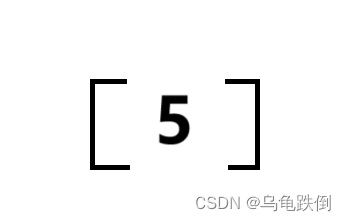
7、同型矩阵


两个矩阵形状一样，称为同型矩阵。即行数和列数相等。


例如：A_{2*3}和B_{2*3}就是同型矩阵。


如果同型矩阵的对应元素相等，那么两个矩阵相等。即相等矩阵的前提是同型矩阵。




二、矩阵与行列式的区别


1、本质上，矩阵是一个数表，而行列式是一个数。


2、符号：矩阵使用 left ( right ) 或者 [ ]，而行列式使用 left | right |


3、形状上，矩阵不一定是方阵，但是行列式一定是一个方阵，即行数等于列数。




三、矩阵的运算


1、加法、减法


对应元素相加减。（注意：只有同型矩阵才能相加减）




矩阵加减法满足的运算法则也很简单:


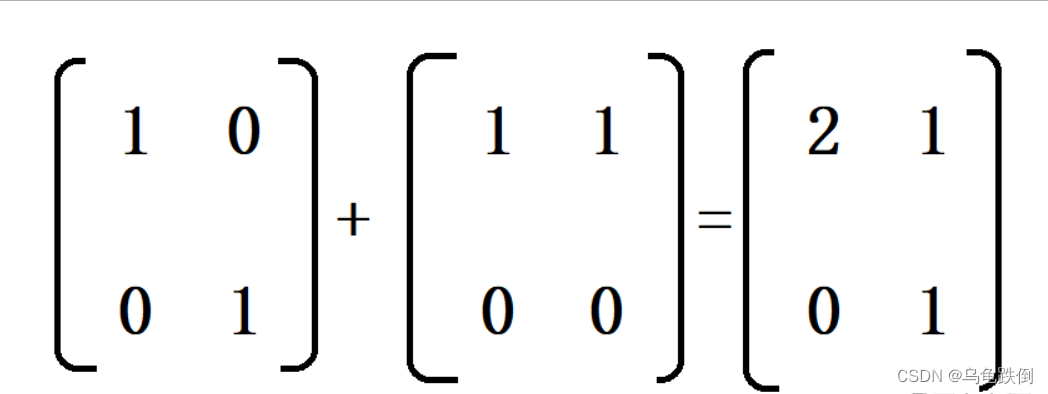
A+B=B+A


(A+B+C) = A+(B+C)


A+(-A)=0


A+B = C Leftrightarrow A = C – B


2、数乘运算


k乘以矩阵的所有元素。




矩阵数乘和行列式的区别


矩阵提公因子：矩阵所有元素均有公因子，公因子朝外提一次


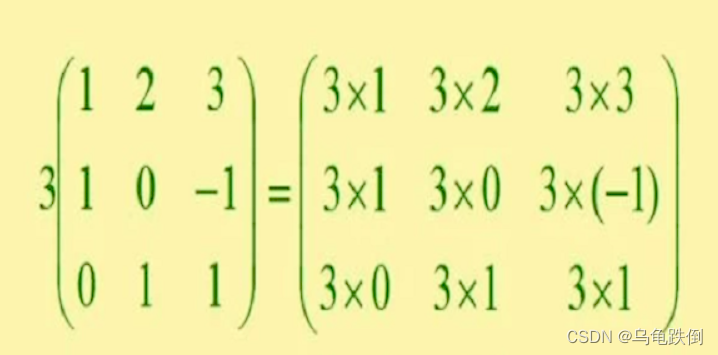
行列式提公因子：一行（或者一列）提取一次，如果所有元素都有公因子，有n行则提n次。


矩阵数乘满足的运算规律：


k(A+B) = kA + kB


(k+m)A = kA + mA


k(mA) = kmA 


四、矩阵乘法


1、矩阵的乘法


第一行乘以第一列，先相乘后相加。


矩阵相乘的前提条件：第一个矩阵的列数等于第二个矩阵的行数。


结果矩阵的形状：结果矩阵的行等于第一个矩阵的行数，结果矩阵的列数等于第二个矩阵的列数。


宋氏七字：中间相等取两头！宋浩线代飞上天！


例如：A_{2*3} * A_{3*2}的结果矩阵就是2*2的方阵。




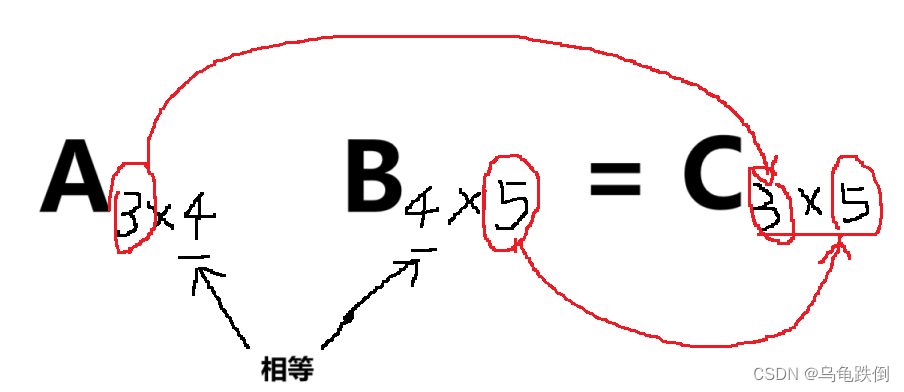
这个实在太刁了，哥们忍不住吟诗一首：


咏宋浩七字口诀


【现】


不用动脑经，不用花一秒。


捏决拿咒间，单走一个6字。


中间相等两头取，宋浩线代飞上天！


从此不愁线代妖，可喜可贺上大分！




做两个小题目练练手：


A_{99*55} * B_{55*200} = C_{99*200}


A_{s*h} * B_{h * m} = C_{s*m}


2、矩阵乘法不满足的三条规律


1）AB  !=  BA   一般不满足交换律 


例如：A_{5*2} B_{2 *3}可以相乘，满足中间相等。但是 B_{2 *3}A_{5*2} 就不可以，因为3和5中间不相等


矩阵乘法一般来说不满足交换，但是也存在交换的情况，此时满足AB = BA,这种情况叫做AB可交换


2）AB = 0 ，且A ！= 0  不能推出  B = 0


如果是数字运算中，xy = 0，可以推出x/y = 0；但是在矩阵运算中不可以


3）AB = AC ,且A ！= 0 不能推出B = C


同样的，在数字运算中，3x= 3y可以推出x=y，但是在矩阵运算中不可以


总结矩阵不满足的三条规律：


(1)AB ! = BA;      


(2)AB = AC,A!=0 不能推出 B = C;  


(3)AB = 0 不能推出A =0或B = 0; 


（任何矩阵和0矩阵相乘都等于0矩阵，由于矩阵乘法的特殊性，需要注意0矩阵的形状）




3、矩阵乘法的运算规律


1）结合律 (AB)C  = A(BC)


2)分配律 (A+B)C = AC + BC       C(A+B) =  CA + CB  （注意，由于矩阵乘法的特殊性，矩阵的左右位置是有严格意义的，不能随意换，即矩阵的乘法不满足交换律）


3）k(AB) = (kA)B = A(kB)    对于一个数字来说，位置可以随意放置


（注意，对于上述三个运算规律来说，要保持矩阵乘法的先后位置，左乘和右乘的位置不能变）


4、矩阵的可交换


当AB = BA ，即A与B可以交换。当题目给你A与B可交换时，就在提醒你AB = BA


（相等矩阵：同型矩阵对应元素相等）


可交换的前提必须是同型方阵。


否则：例如A_{2*3} B_{3*2} = C_{2*2}       AB的结果矩阵是2✖2的矩阵


                   B_{3*2}A_{2*3} = C_{3*3}        BA的结果矩阵式3✖3的矩阵


   这里结果明显是不相等的！所以，如果不是同型方阵是不可以交换的。首先结果矩阵的形状就要出错


五、矩阵的幂运算


（注意：矩阵的幂运算必须是方阵,保证连续运算）


矩阵的幂运算：A^{k} = AA…A   


其中A^{_{0}} = E


性质1）A^{^k{1}} A^{k^{_{2}}} = A^{^{k1 + k2}}


性质2）(A^{^{k1}})^{^{k2}} = A^{^{k1k2}}




(再次注意：矩阵的乘法不满足交换律)


 (AB)^{k^{}}  ! = A^{^{k}}B^{^{k}}


例如：(AB)^{^{2}} != A^{_{2}} B^{^{2}} 


 为什么不相等？


因为：(AB)^{^{2}} = ABAB


          A^{_{2}} B^{^{2}}   =  AABB


我们永远要记住：矩阵的乘法不满足交换律，因此上式明显式不相等的。


除非AB可交换，即AB = BA.




同时：


(A+B)^{^{2}} !=  A^{_{2}} + 2AB + B^{^{2}}


证明：(A+B)(A+B) = (A+B)A + (A+B)B = A^{_{2}} + BA + AB + B^{^{2}}


很明显，2AB ！= BA + AB 




同理：


(A-B)^{2^{}}  != A^{_{2}} – 2AB + B^{^{2}}


证明：(A-B)(A-B) = (A-B)A – (A-B)B = A^{_{2}} – BA – AB + B^{^{2}}


很明显，2AB ！= -BA – AB 




永远记住！！！！！！！


矩阵乘法要严格注意AB的先后位置，位置的变化是会影响运算结果的


（因为矩阵的乘法是第一个矩阵的行   乘以    第二个矩阵的列）




但是，对于(A + E)^{2^{}} =  A^{_{2}} + AE + EA + B^{^{2}}


                  (A - E)^{2^{}} = A^{_{2}} – AE – EA + B^{^{2}}


                 对于上两式来说，


任何矩阵乘以单位阵E的等于其本身，而对于单位阵来说，左乘和右乘是一样的。


故而，AE = EA , BE =EB


所以：


                  (A + E)^{2^{}} =  A^{_{2}} + 2AE + B^{^{2}}


                  (A - E)^{2^{}} = A^{_{2}} – 2AE  + B^{^{2}}


                    是成立的！




六、简单的矩阵运算，学到的知识点运用起来。


例如


给两个方程组：x1  = y1 -y2            y1 = z1 + z2 + z3


                         x2 = y1 + y2           y2 = z1 -2z2 + z3


要求x1 和 x2 用z1 z2 z3表示












 原文地址:https://blog.csdn.net/qq_51216031/article/details/134521526 


本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。


如若转载，请注明出处：http://www.7code.cn/show_30924.html 


如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！





	

		

            
                            
            			
		

		


            
			            
			                
                        
            
		

	




      

          

    

  






	

            	

            
                

                

                    上一篇
                    一文例说嵌入式 C 程序的内聚和耦合
                

             
        

                    	

            
                

                    下一篇
                    探究C语言中的分支和循环语句
                

                

            
        

            


    

        
相关文章

        

                      

              
          

                      

              
          

                      

              
          

                      

              
          

                      

              
          

                      

              
          

                      

              
          

                      

              
          

                  

    





    	

		
发表回复 
您的邮箱地址不会被公开。 必填项已用 * 标注
插入图片





 浏览器会保存昵称、邮箱和网站cookies信息，下次评论时使用。