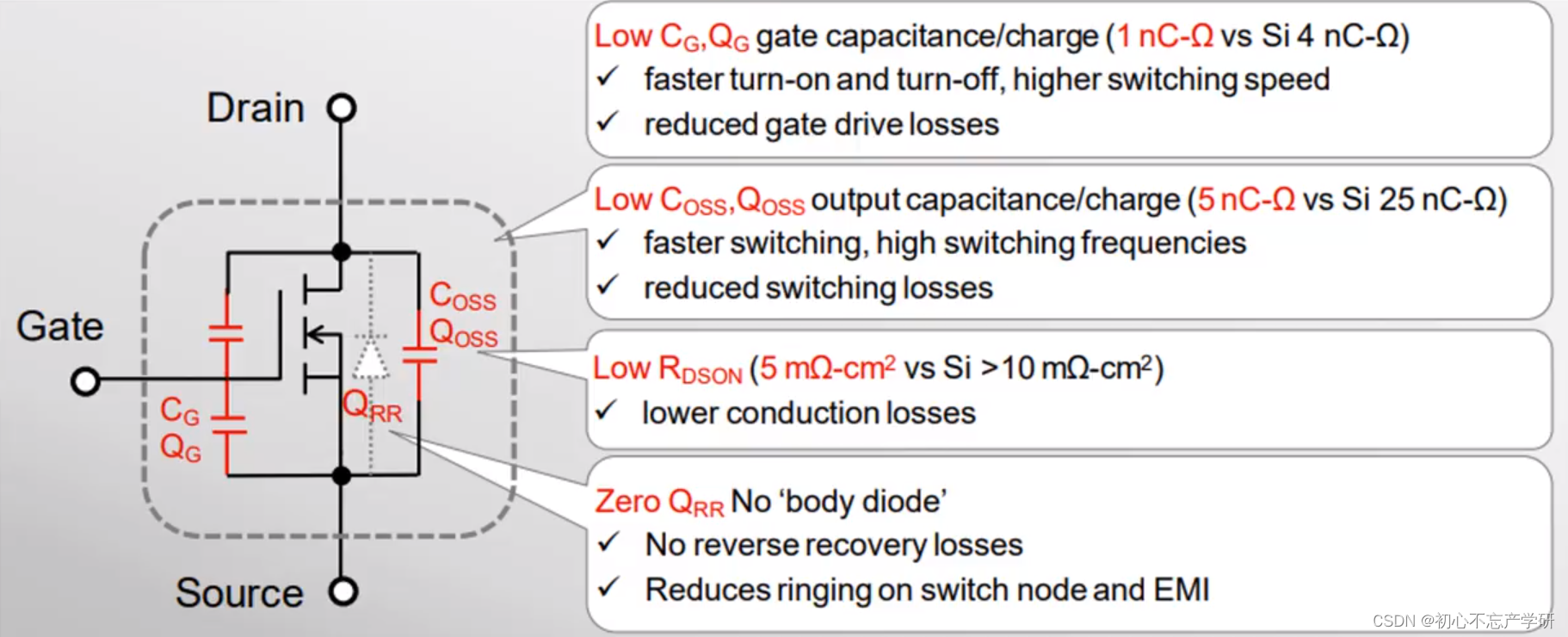
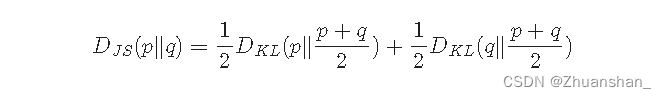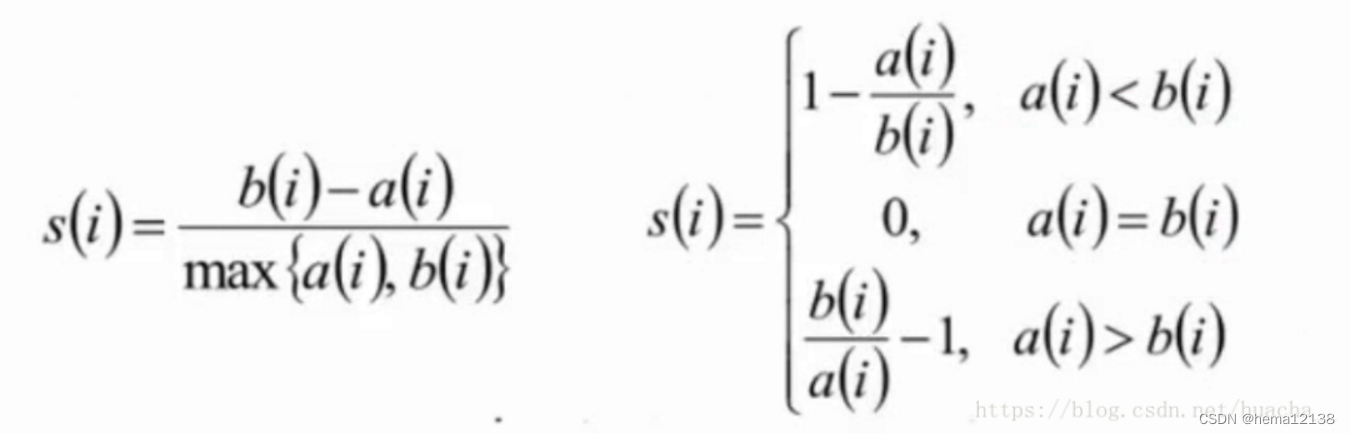数学基础
KL散度
JS散度
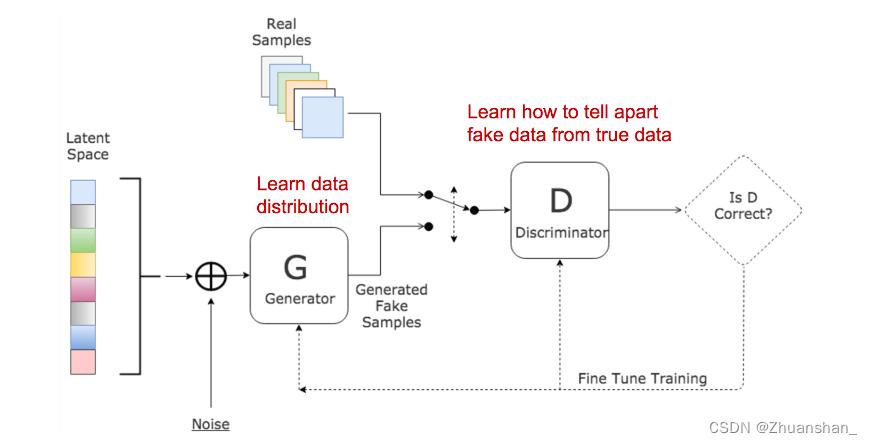
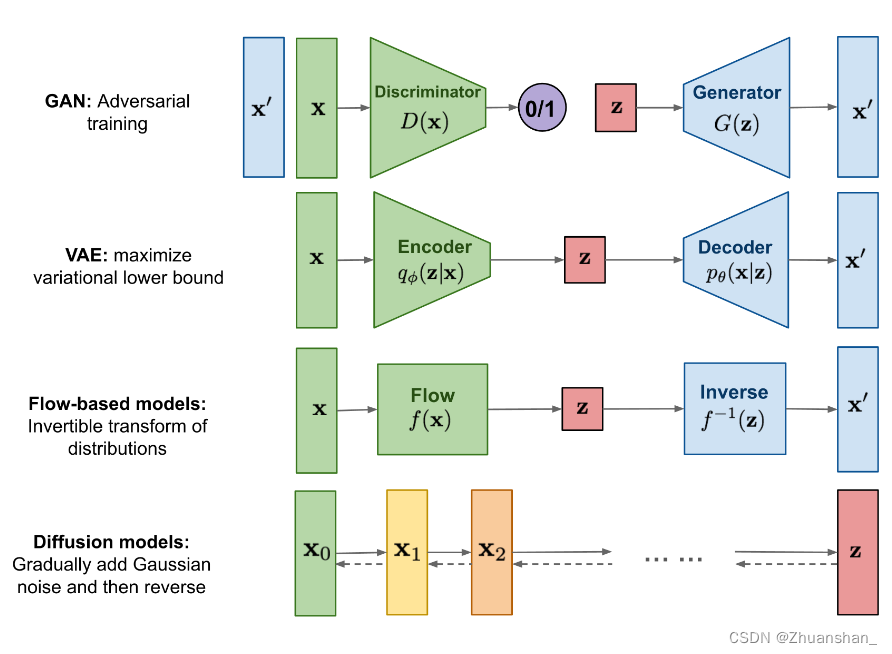
GAN
鉴别器D
生成器G
Autoencoder
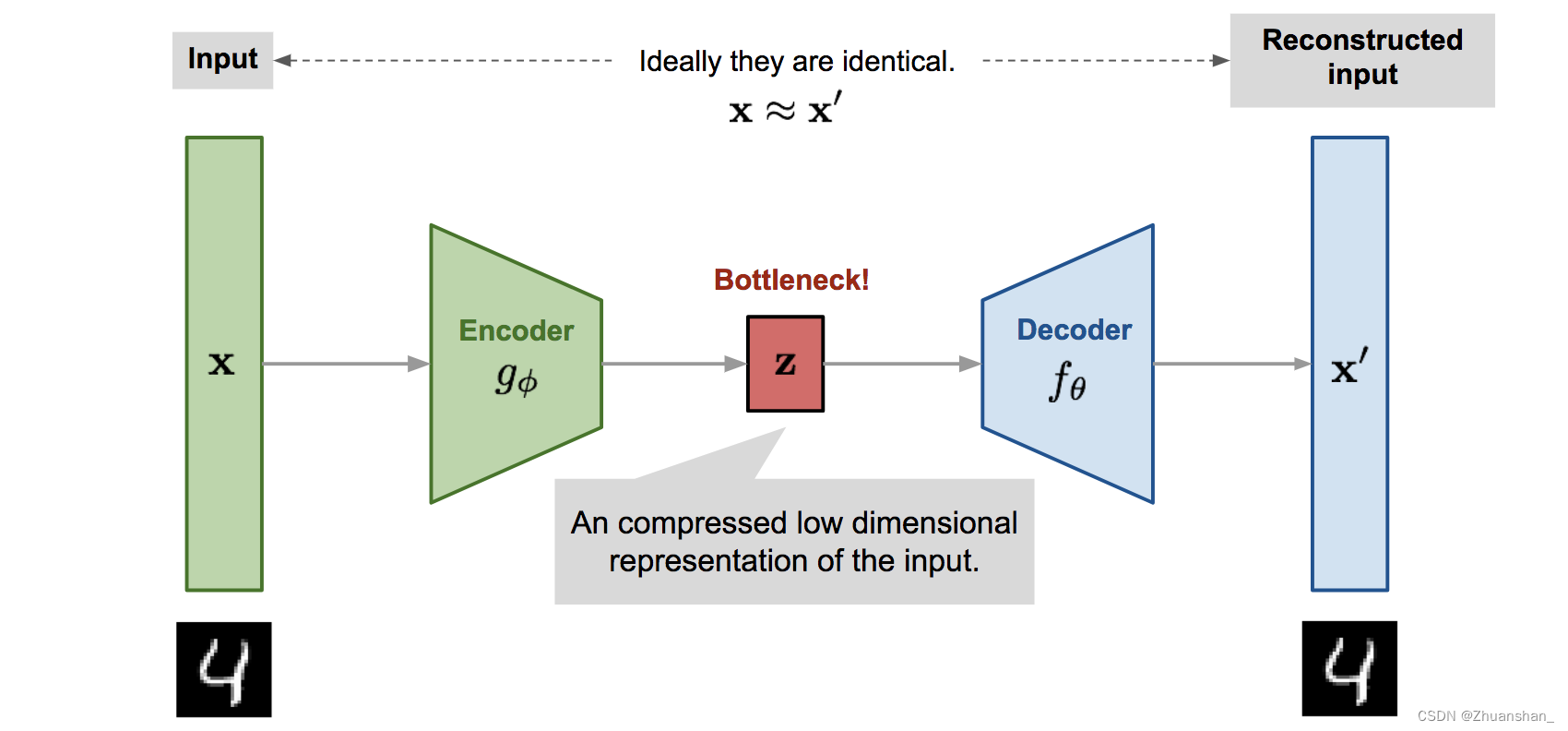
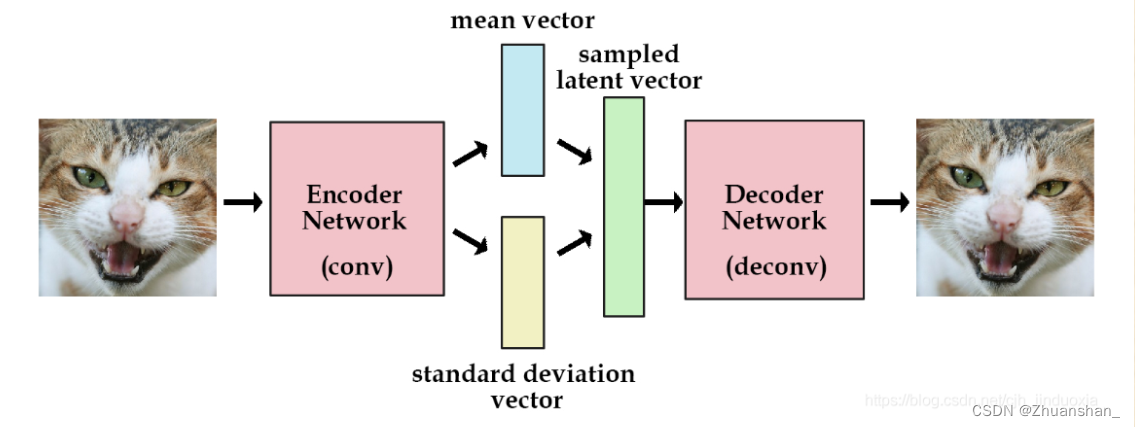
VAE
- 其思想和其他自编码器模型不同，主要用到变分贝叶斯和图形模型
- VAE通过对Encoder对输入（我们这里以图片为输入）进行高效编码，然后由Decoder使用编码还原出图片，在理想情况下，还原输出的图片应该与原图片极相近。
Diffusion Model
- GAN因为使用对抗训练，训练不稳定，缺少多样性生成；VAE依赖于替代损失；流模型必须使用专门的体系结构来构造可逆转换
- 扩散模型受非平衡热力学启发，其定义了一个马尔可夫链，通过像数据中添加噪声，然后反向学习扩散过程，进而构造样本
Forward diffusion process
- 给定从真实数据中采样的数据点，并向样本中添加少量高斯噪声，产生一系列的有噪声的样本
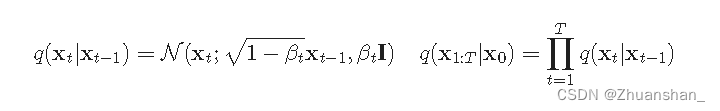
- 随着t逐渐变大，数据样本逐渐失去可区分的特征，最终当T趋于无穷时，
X
T
X_T
XT等价于正态高斯分布
- 可以推出
x
xt的推导公式，而当样本逐渐变得嘈杂时，更新步幅也随之变大
- 其中
=
1
−
β
at=1−βt,β
β逐渐变大，从0.0001到0.002之间，进而α
α也逐渐变小 - 可以看到
x
t
x_t
xt的公式中x
t
x_t
xt与x
t
−
1
x_{t-1}
xt−1有关，同时再加上一点高斯分布噪音
- 同理，
x
t
−
1
x_{t-1}
xt−1也可以用x
t
−
2
x_{t-2}
xt−2表示出来，带入到x
t
x_t
xt的表达式中，得到红线部分z
1
,
z
2
z_1,z_2
z1,z2两个高斯分布噪音的相加 - 式子中对高斯分布乘上一个数，相当于对分布的方差进行变化，如果加减操作，相当于对分布的均值发生变化，因此可以发现二者的方差已经变化
- 相乘之后的分布仍服从高斯分布，因此二者可以做加法，新的分布还是高斯分布，只不过是方差相加
- 因此可以看出，
x
t
x_t
xt的分布和他的前t项相关，是其前t项连乘，这样就能做到直接得到加噪过程中任意一项的图像分布。
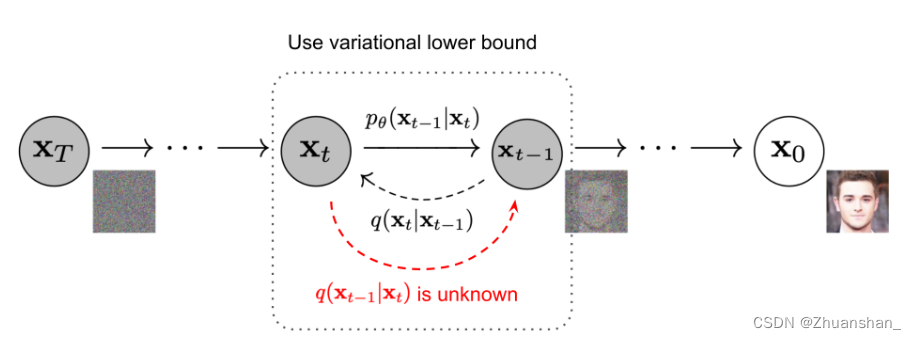
Reverse Process
- 反向过程即通过
x
t
x_t
xt逐渐推出x
0
x_0
x0的过程，通过使用贝叶斯公式可以完成这一过程，其中q
(
x
t
∣
x
t
−
1
)
q(x_t|x_{t-1})
q(xt∣xt−1)为正向过程，已知，q
(
x
t
−
1
∣
∣
x
0
)
q(x_{t-1|}|x_0)
q(xt−1∣∣x0)也都已知 - 这里三个式子都是服从高斯分布，因此乘以一个数和加上一个数，分别改变其方差和均值，和前面的过程相同。
- 根据贝叶斯公式，需要将其中两项相乘，再除以第三项，因为这三项都服从正态分布，因此将他们做乘除即幂次相加减
- 通过对方程进行化简，可以配方得到关于
x
t
−
1
x_{t-1}
xt−1的式子，而关于正态分布的公式进行展开，可以得到和配方后的式子相同的式子
- 因此，可以分别得到
σ
和
μ
σ和μ的值
- 其中，
x
0
x_0
x0不知道，但是通过前向过程可以将x
0
x_0
x0逆推回来，并将其带入均值方程，可以得到均值的最终结果。此时，均值只与x
t
x_t
xt有关 - 另外，可以看到均值和
z
t
z_t
zt噪声有关。在反向过程中，利用前向过程提供的每一步所添加的噪音当作标签进行训练，进而进行拟合，估计出噪声z
t
z_t
zt。
参考资料
原文地址:https://blog.csdn.net/weixin_44796129/article/details/134663193
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.7code.cn/show_31114.html
如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！
