专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶
一起努力
1.前言
在前面我们学习了关于顺序表,链表,栈,队列的存储方式。今天我将给大家带来关于树的一些内容以及堆的部分内容,详细包括树的定义,树相关的概念,二叉树和满二叉树的概念,树代码的实现会在后面的内容,大堆和小堆的代码实现。今天的内容相较于前面会有一点难以理解,希望大家可以认真学习,当然还有几个力扣刷题的函数扩展,其中的内容就绝对会让你感到其中的乐趣。
2.树
2.1概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。有一个特殊的结点,称为根结点,根节点没有前驱结点除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继因此,树是递归定义的。
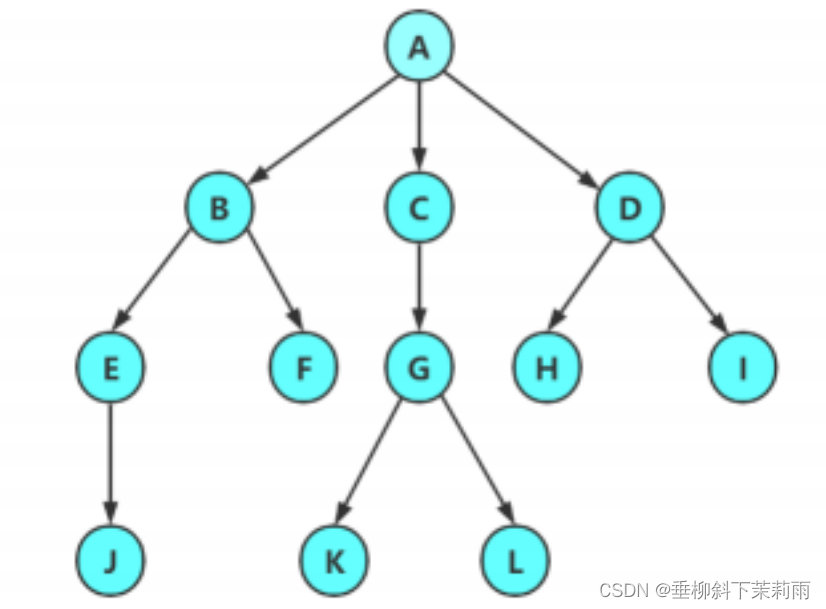
下面我给出关于树的图:
2.2树的相关概念
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林。
3.堆
3.1堆的概念
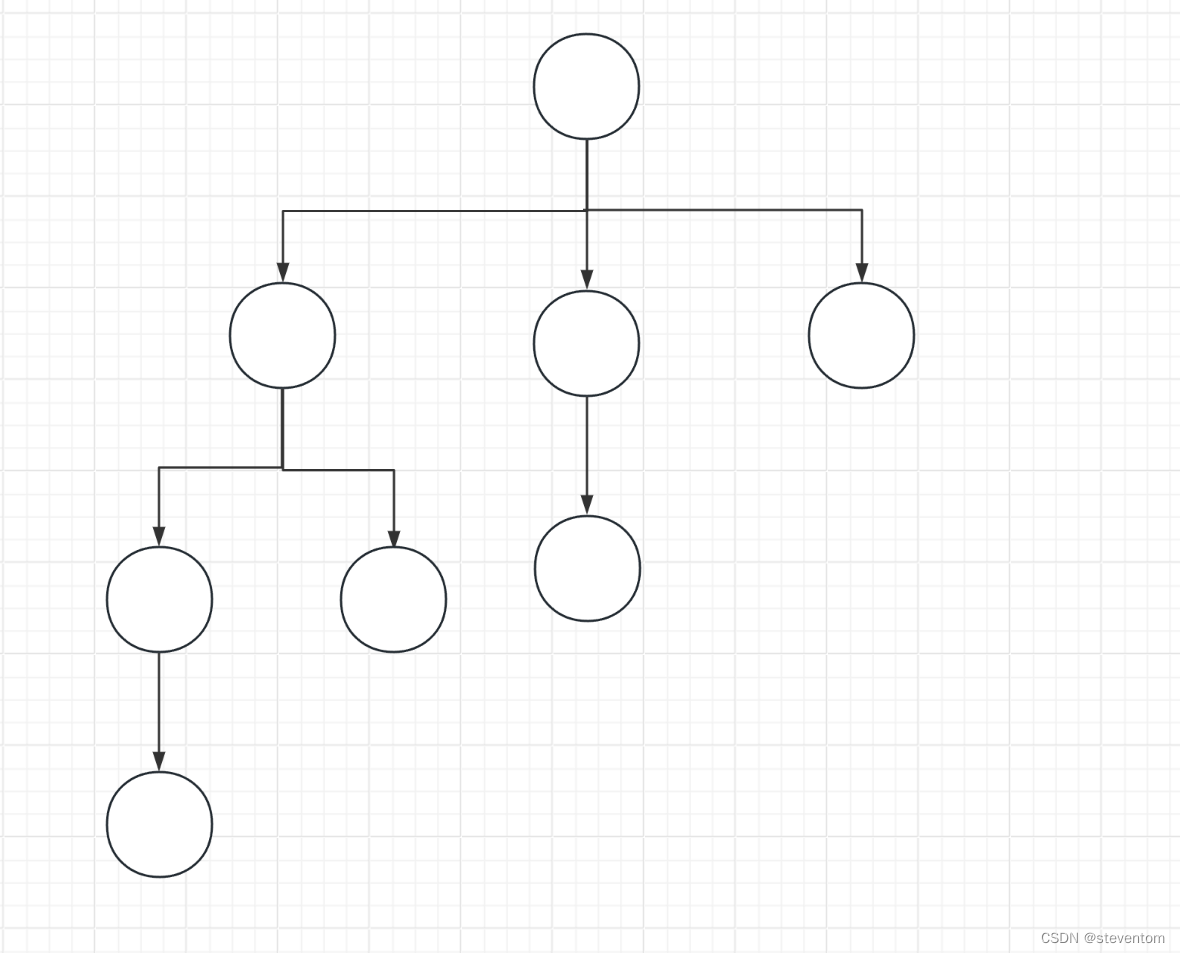
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1, 2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。堆我们分为大堆个小堆,大堆是父节点永远大于子节点,小堆是父节点永远小于子节点。堆的图我们认为堆是如下的样子:

事实上我们是顺序表的形式存储的,我们知道堆是一颗完全二叉树,我们将树的每个节点用数字进行标记,如下:

我们不难得出我们知道父节点的编号为n,左孩子的编号为2n+1,右孩子的编号为2n+2,假设左孩子的标号为n那么父节点的编号为(n-1)/2,我们设右孩子的节点为n那么父节点的编号为(n-1)/2,那我们很容易得到孩子节点编号为n父节点的编号为(n-1)/2,根据这一特点我们就可以利用顺序表进行存储,这样也能更好的找到父节点和孩子节点的位置,接下来我们以实现小堆为例子来展示一下大堆和小堆的实现(大堆和小堆的差距只有向上调整的部分符号不同,其余基本一致)。
3.2小堆函数实现
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void Swap(MyHeapData* num1, MyHeapData* num2)
{
MyHeapData temp = *num1;
*num1 = *num2;
*num2 = temp;
}
void AdJustUp(MyHeapData* arr, int size)
{
assert(arr);
int child = size - 1, parent = (child - 1) / 2;
while (child > 0)
{
if (arr[child] < arr[parent])
{
Swap(&arr[child], &arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
void HeapInit(Heap* php)
{
assert(php);
php->data = (MyHeapData*)malloc(sizeof(MyHeapData));
php->size = 0;
php->capacity = 0;
}
void HeapDestory(Heap* php)
{
assert(php);
free(php->data);
php->data = NULL;
}
void HeapPush(Heap* php, MyHeapData x)
{
if (php->size == php->capacity)
{
int newcapacity = php->capacity + 2;
MyHeapData* arr = (MyHeapData*)realloc(php->data, newcapacity * sizeof(MyHeapData));
if (arr == NULL)
{
perror("realloc fail");
return;
}
php->data = arr;
php->capacity = newcapacity;
}
php->data[php->size++] = x;
AdJustUp(php->data, php->size);
}
void print(Heap* php)
{
for (int i = 0; i < php->size; i++)
printf("%d ", php->data[i]);
}
void HeapPop(Heap* php)
{
assert(php);
if (!HeapEmpty(php))
{
Swap(&php->data[0], &php->data[php->size - 1]);
php->size--;
AdJustDown(php->data, php->size);
}
}
void AdJustDown(MyHeapData* arr, int size)
{
assert(arr);
int parent = 0, child = parent * 2 + 1;
while (child<size)
{
if (child + 1 < size && arr[child] > arr[child + 1])
{
child++;
}
Swap(&arr[parent], &arr[child]);
parent = child;
child = parent * 2 + 1;
}
}
bool HeapEmpty(Heap* php)
{
assert(php);
return php->size == 0;
}
void text()
{
Heap ph;
HeapInit(&ph);
HeapPush(&ph, 7);
HeapPush(&ph, 6);
HeapPush(&ph, 4);
HeapPush(&ph, 5);
HeapPush(&ph, 1);
HeapPush(&ph, 1);
HeapPush(&ph, 3);
print(&ph);
printf("n");
HeapPop(&ph);
print(&ph);
printf("n");
HeapPop(&ph);
print(&ph);
HeapDestory(&ph);
}4.力扣刷题函数
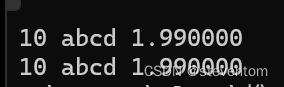
函数为sscanf函数和sprintf函数,其中sscanf函数是将任意类型数据储存在字符串中,spintf函数是将字符串数据输入到新的变量中,他们重新定义了输入输出流,我们看下面代码来感受一下:
#include<stdio.h>
int main()
{
int a = 10;
char arr[] = "abcd";
double f = 1.99;
char brr[100];
sprintf(brr, "%d %s %f", a, arr, f);
printf("%sn", brr);
a = 0;
double b = 0.0;
sscanf(brr, "%d %s %f", &a, &arr, &b);
printf("%d %s %f", a, arr, f);
return 0;
}
5.总结
今天的内容到这里就结束了,非常感谢大家的观看,希望大家可一学到很多东西,尤其是堆的向下调整和向上调整这两个函数。
原文地址:https://blog.csdn.net/Infernal_Puppet/article/details/134683026
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_32450.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!