什么是并查集
并查集是一种数据结构,用于处理一些不交集的合并及查询问题。它支持两种操作:
查找(Find):确定某个元素属于哪个子集。它可以用来判断两个元素是否属于同一个子集。
合并(Union):将两个子集合并成一个集合。
并查集的功能
将连通边加入并查集
在join函数中 我们需要先寻找 u 和 v 的根,然后再进行连线在一起,而不是直接 用 u 和 v 连线在一起。
// 将v,u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}
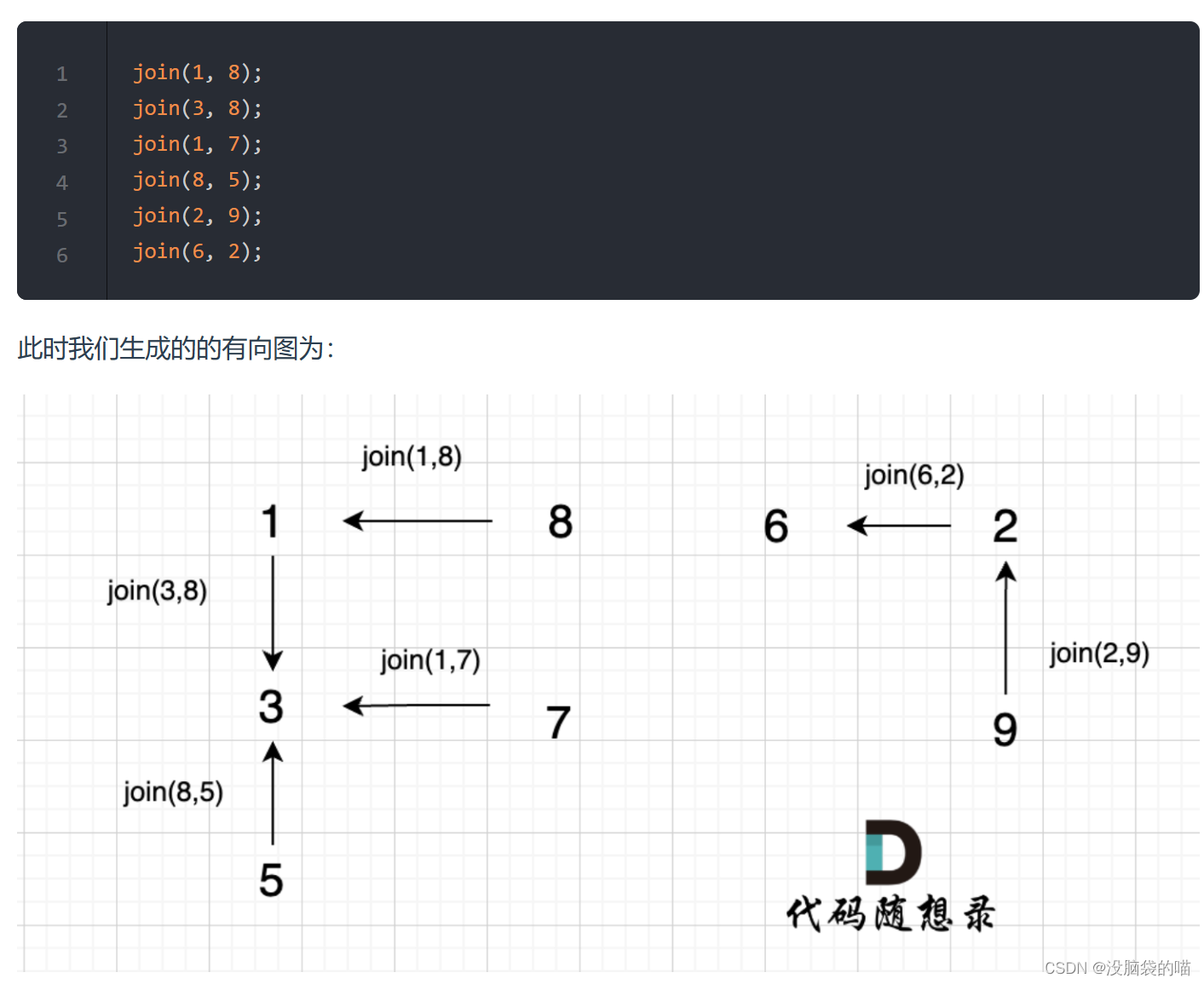
并查集里寻根的过程
int find(int u) {
if (u == father[u]) return u; // 如果根就是自己,直接返回
else return find(father[u]); // 如果根不是自己,就根据数组下标一层一层向下找
}
并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
路径压缩:所有节点直接指向根节点
只需要在递归的过程中,让 father[u] 接住 递归函数 find(father[u]) 的返回结果。
因为 find 函数向上寻找根节点,father[u] 表述 u 的父节点,那么让 father[u] 直接获取 find函数 返回的根节点,这样就让节点 u 的父节点 变成根节点。
int find(int u) {
if (u == father[u]) return u;
else return father[u] = find(father[u]); // 路径压缩
}
1971. 寻找图中是否存在路径
**题目:**有一个具有 n 个顶点的 双向 图,其中每个顶点标记从 0 到 n – 1(包含 0 和 n – 1)。图中的边用一个二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接,并且没有顶点存在与自身相连的边。
请你确定是否存在从顶点 source 开始,到顶点 destination 结束的 有效路径 。
给你数组 edges 和整数 n、source 和 destination,如果从 source 到 destination 存在 有效路径 ,则返回 true,否则返回 false 。
题目链接: 1971. 寻找图中是否存在路径
代码如下:
class Solution {
public int[] father;
public int find(int u) {
if (u == father[u]) return u; // 如果根就是自己,直接返回
else return find(father[u]); // 如果根不是自己,就根据数组下标一层一层向下找
}
public void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}
public boolean isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
public boolean validPath(int n, int[][] edges, int source, int destination) {
father=new int[n];
for (int i = 0; i < n; i++) {
father[i] = i;
}
for(int i=0;i<edges.length;i++){
join(edges[i][0],edges[i][1]);
}
return isSame(source,destination);
}
}
原文地址:https://blog.csdn.net/weixin_44925329/article/details/134709280
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_32650.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!