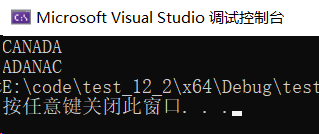
本文介绍: 写一个判断素数的函数,在主函数输入一个整数,输出是否素数的信息写一个函数,使给定的一个 3X3 的二维整型数组转置,即行列互换。写一个函数,使输入的一个字符串按反序存放,如输入”CANADA”,输出“ADANAC”。在主函数中输入和输出字符串。写一个函数,将两个字符串连接,如字符串 1 是”BEI”,字符串 2 是”JING”,连接起来是”BEIJING”
第七章 函数
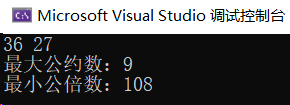
7.1 最大公约数和最小公倍数
题目概述:
写两个函数,分别求两个整数的最大公约数和最小公倍数,用主函数调用这两个函数,并输出结果。两个整数由键盘输入。
题目思路:
代码实现:
7.2 函数判断素数
题目概述:
写一个判断素数的函数,在主函数输入一个整数,输出是否素数的信息
题目思路:
代码实现:
优化1:由于偶数都不是素数,我们可以只从奇数项开始,每个数加+2让下一个也是奇数
优化2:当一个数不是素数的时候,一定能下成下列的一个式子,且他是可以被一个因子整除的
例:m = a *b
16 = 4 * 4
16 = 2 * 8
a和b中一个数字是 <= sqrt(m) →[4]
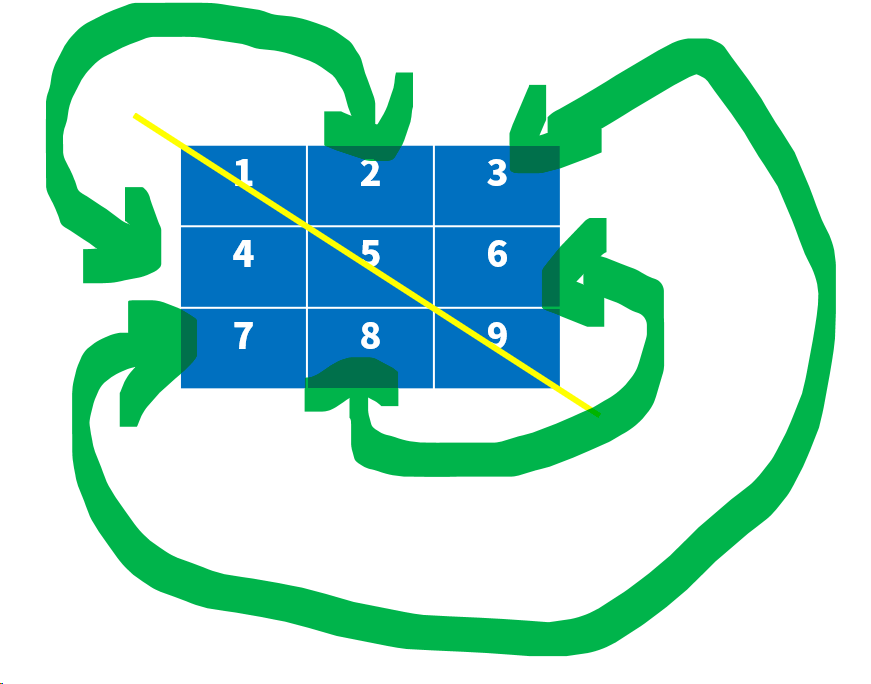
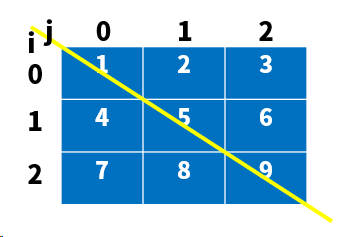
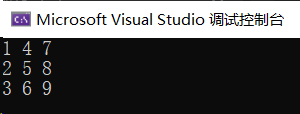
7.3 行列互换
题目概述:
题目思路:
代码实现:
7.4 反序存放字符串
题目概述:
题目思路:
代码实现:
7.5 函数连接字符串
题目概述:
题目思路:
代码实现:
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。