9. 双向队列

本文介绍: 在队列中，我们仅能删除头部元素或在尾部添加元素。如下图所示，双向队列(double–end e d queue)提供了更高的灵活性，允许在头部和尾部执行元素的添加或删除操作。

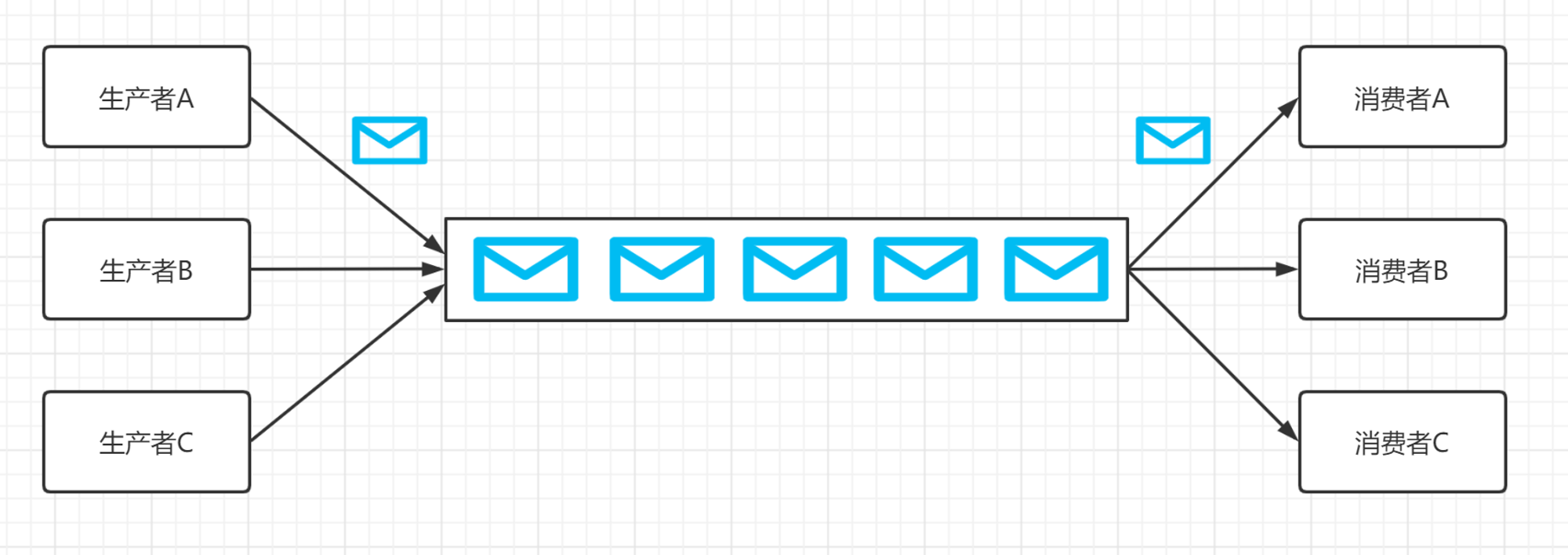
在队列中，我们仅能删除头部元素或在尾部添加元素。如下图所示，双向队列(double–end e d queue)提供了更高的灵活性，允许在头部和尾部执行元素的添加或删除操作。

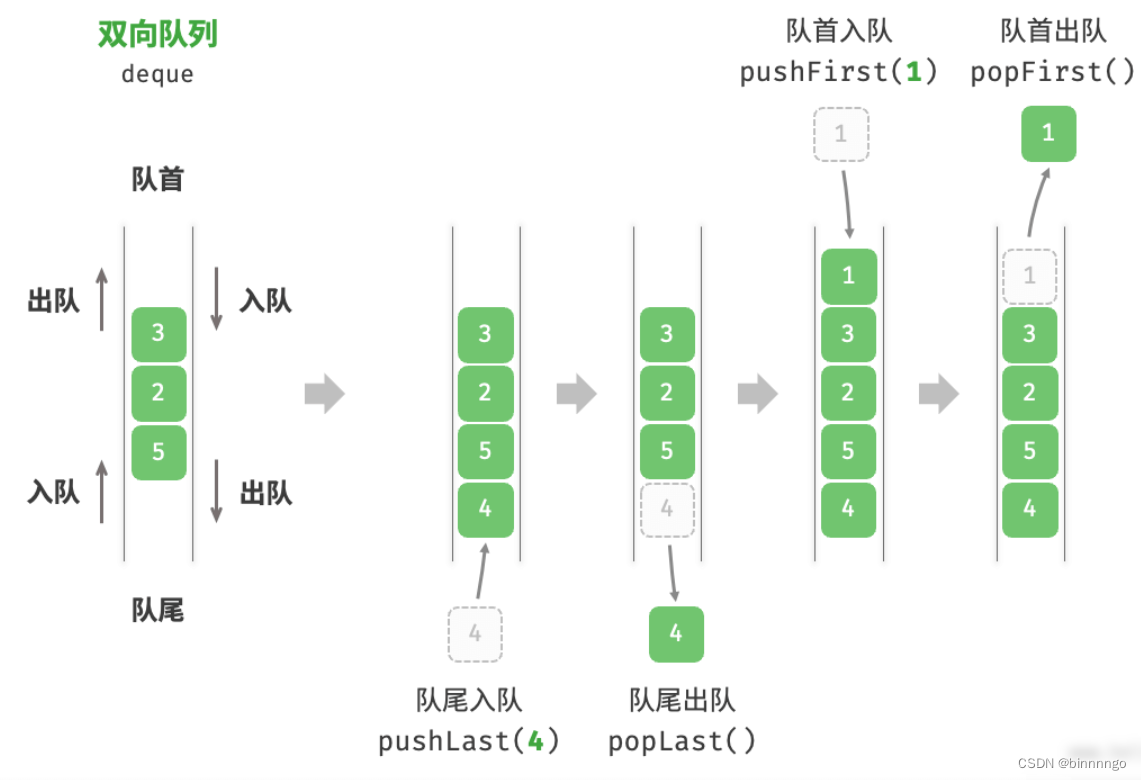
9.1 双向队列常用操作

/* 初始化双向队列 */
deque&lt;int&gt; deque;

/* 元素入队 */
deque.push_back(2);   // 添加至队尾
deque.push_back(5);
deque.push_back(4);
deque.push_front(3);  // 添加至队首
deque.push_front(1);

/* 访问元素 */
int front = deque.front(); // 队首元素
int back = deque.back();   // 队尾元素

/* 元素出队 */
deque.pop_front();  // 队首元素出队
deque.pop_back();   // 队尾元素出队

/* 获取双向队列的长度 */
int size = deque.size();

/* 判断双向队列是否为空 */
bool empty = deque.empty();

9.2 双向队列实现

双向队列的实现与队列类似，可以选择链表或数组作为底层数据结构。

9.2.1 基于双向链表的实现

回顾上一节内容，我们使用普通单向链表来实现队列，因为它可以方便地删除头节点（对应出队操作）和在尾节点后添加新节点（对应入队操作）。

对于双向队列而言，头部和尾部都可以执行入队和出队操作。换句话说，双向队列需要实现另一个对称方向的操作。为此，我们采用“双向链表”作为双向队列的底层数据结构。

如下图所示，我们将双向链表的头节点和尾节点视为双向队列的队首和队尾，同时实现在两端添加和删除节点的功能。

实现代码如下所示：

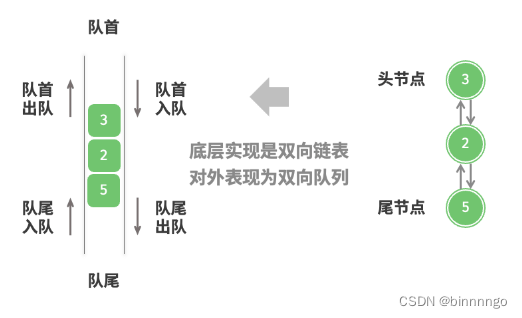
/* 双向链表节点 */
struct DoublyListNode {
    int val;              // 节点值
    DoublyListNode *next; // 后继节点指针
    DoublyListNode *prev; // 前驱节点指针
    DoublyListNode(int val) : val(val), prev(nullptr), next(nullptr) {
    }
};

/* 基于双向链表实现的双向队列 */
class LinkedListDeque {
  private:
    DoublyListNode *front, *rear; // 头节点 front ，尾节点 rear
    int queSize = 0;              // 双向队列的长度

  public:
    /* 构造方法 */
    LinkedListDeque() : front(nullptr), rear(nullptr) {
    }

    /* 析构方法 */
    ~LinkedListDeque() {
        // 遍历链表删除节点，释放内存
        DoublyListNode *pre, *cur = front;
        while (cur != nullptr) {
            pre = cur;
            cur = cur-&gt;next;
            delete pre;
        }
    }

    /* 获取双向队列的长度 */
    int size() {
        return queSize;
    }

    /* 判断双向队列是否为空 */
    bool isEmpty() {
        return size() == 0;
    }

    /* 入队操作 */
    void push(int num, bool isFront) {
        DoublyListNode *node = new DoublyListNode(num);
        // 若链表为空，则令 front 和 rear 都指向 node
        if (isEmpty())
            front = rear = node;
        // 队首入队操作
        else if (isFront) {
            // 将 node 添加至链表头部
            front-&gt;prev = node;
            node-&gt;next = front;
            front = node; // 更新头节点
        // 队尾入队操作
        } else {
            // 将 node 添加至链表尾部
            rear-&gt;next = node;
            node->prev = rear;
            rear = node; // 更新尾节点
        }
        queSize++; // 更新队列长度
    }

    /* 队首入队 */
    void pushFirst(int num) {
        push(num, true);
    }

    /* 队尾入队 */
    void pushLast(int num) {
        push(num, false);
    }

    /* 出队操作 */
    int pop(bool isFront) {
        if (isEmpty())
            throw out_of_range("队列为空");
        int val;
        // 队首出队操作
        if (isFront) {
            val = front->val; // 暂存头节点值
            // 删除头节点
            DoublyListNode *fNext = front->next;
            if (fNext != nullptr) {
                fNext->prev = nullptr;
                front->next = nullptr;
                delete front;
            }
            front = fNext; // 更新头节点
        // 队尾出队操作
        } else {
            val = rear->val; // 暂存尾节点值
            // 删除尾节点
            DoublyListNode *rPrev = rear->prev;
            if (rPrev != nullptr) {
                rPrev->next = nullptr;
                rear->prev = nullptr;
                delete rear;
            }
            rear = rPrev; // 更新尾节点
        }
        queSize--; // 更新队列长度
        return val;
    }

    /* 队首出队 */
    int popFirst() {
        return pop(true);
    }

    /* 队尾出队 */
    int popLast() {
        return pop(false);
    }

    /* 访问队首元素 */
    int peekFirst() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return front->val;
    }

    /* 访问队尾元素 */
    int peekLast() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return rear->val;
    }

    /* 返回数组用于打印 */
    vector<int> toVector() {
        DoublyListNode *node = front;
        vector<int> res(size());
        for (int i = 0; i < res.size(); i++) {
            res[i] = node->val;
            node = node->next;
        }
        return res;
    }
};

9.2.2 基于 数组的实现

如下图所示，与基于数组实现队列类似，我们也可以使用环形数组来实现双向队列。

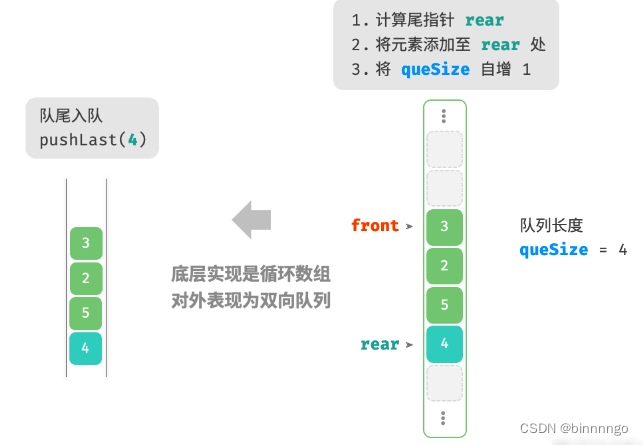
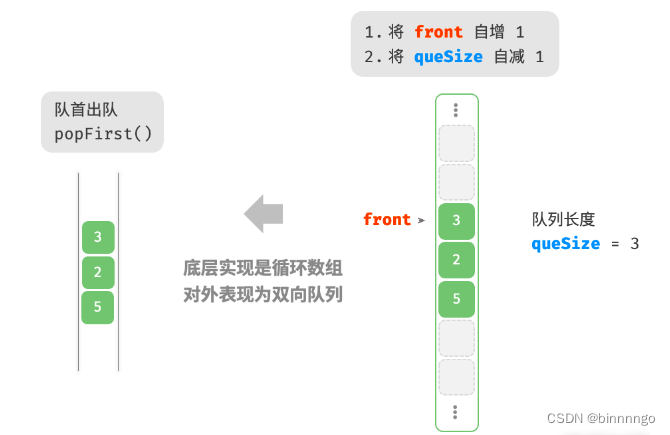
在队列的实现基础上，仅需增加“队首入队”和“队尾出队”的方法：

/* 基于环形数组实现的双向队列 */
class ArrayDeque {
  private:
    vector<int> nums; // 用于存储双向队列元素的数组
    int front;        // 队首指针，指向队首元素
    int queSize;      // 双向队列长度

  public:
    /* 构造方法 */
    ArrayDeque(int capacity) {
        nums.resize(capacity);
        front = queSize = 0;
    }

    /* 获取双向队列的容量 */
    int capacity() {
        return nums.size();
    }

    /* 获取双向队列的长度 */
    int size() {
        return queSize;
    }

    /* 判断双向队列是否为空 */
    bool isEmpty() {
        return queSize == 0;
    }

    /* 计算环形数组索引 */
    int index(int i) {
        // 通过取余操作实现数组首尾相连
        // 当 i 越过数组尾部后，回到头部
        // 当 i 越过数组头部后，回到尾部
        return (i + capacity()) % capacity();
    }

    /* 队首入队 */
    void pushFirst(int num) {
        if (queSize == capacity()) {
            cout << "双向队列已满" << endl;
            return;
        }
        // 队首指针向左移动一位
        // 通过取余操作，实现 front 越过数组头部后回到尾部
        front = index(front - 1);
        // 将 num 添加至队首
        nums[front] = num;
        queSize++;
    }

    /* 队尾入队 */
    void pushLast(int num) {
        if (queSize == capacity()) {
            cout << "双向队列已满" << endl;
            return;
        }
        // 计算尾指针，指向队尾索引 + 1
        int rear = index(front + queSize);
        // 将 num 添加至队尾
        nums[rear] = num;
        queSize++;
    }

    /* 队首出队 */
    int popFirst() {
        int num = peekFirst();
        // 队首指针向后移动一位
        front = index(front + 1);
        queSize--;
        return num;
    }

    /* 队尾出队 */
    int popLast() {
        int num = peekLast();
        queSize--;
        return num;
    }

    /* 访问队首元素 */
    int peekFirst() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return nums[front];
    }

    /* 访问队尾元素 */
    int peekLast() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        // 计算尾元素索引
        int last = index(front + queSize - 1);
        return nums[last];
    }

    /* 返回数组用于打印 */
    vector<int> toVector() {
        // 仅转换有效长度范围内的列表元素
        vector<int> res(queSize);
        for (int i = 0, j = front; i < queSize; i++, j++) {
            res[i] = nums[index(j)];
        }
        return res;
    }
};

9.3 双向队列应用

双向队列兼具栈与队列的逻辑，因此它可以实现这两者的所有应用场景，同时提供更高的自由度。

我们知道，软件的“撤销”功能通常使用栈来实现：系统将每次更改操作 push 到栈中，然后通过 pop 实现撤销。然而，考虑到系统资源的限制，软件通常会限制撤销的步数（例如仅允许保存 (50) 步）。当栈的长度超过 (50) 时，软件需要在栈底（队首）执行删除操作。但栈无法实现该功能，此时就需要使用双向队列来替代栈。请注意，“撤销”的核心逻辑仍然遵循栈的先入后出原则，只是双向队列能够更加灵活地实现一些额外逻辑。