加载 MNIST 数据库
from keras.datasets import mnist
# 使用 Keras 导入MNIST 数据库
(X_train, y_train), (X_test, y_test) = mnist.load_data()
print("The MNIST database has a training set of %d examples." % len(X_train))
print("The MNIST database has a test set of %d examples." % len(X_test))将前六个训练图像可视化
import matplotlib.pyplot as plt
%matplotlib inline
import matplotlib.cm as cm
import numpy as np
# 绘制前六幅训练图像
fig = plt.figure(figsize=(20,20))
for i in range(6):
ax = fig.add_subplot(1, 6, i+1, xticks=[], yticks=[])
ax.imshow(X_train[i], cmap='gray')
ax.set_title(str(y_train[i]))
查看图像的更多细节
def visualize_input(img, ax):
ax.imshow(img, cmap='gray')
width, height = img.shape
thresh = img.max()/2.5
for x in range(width):
for y in range(height):
ax.annotate(str(round(img[x][y],2)), xy=(y,x),
horizontalalignment='center',
verticalalignment='center',
color='white' if img[x][y]<thresh else 'black')
fig = plt.figure(figsize = (12,12))
ax = fig.add_subplot(111)
visualize_input(X_train[0], ax) 预处理输入图像:通过将每幅图像中的每个像素除以 255 来调整图像比例
预处理输入图像:通过将每幅图像中的每个像素除以 255 来调整图像比例
# 调整比例,使数值在 0 - 1 范围内 [0,255] --> [0,1]
X_train = X_train.astype('float32')/255
X_test = X_test.astype('float32')/255
print('X_train shape:', X_train.shape)
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')对标签进行预处理:使用单热方案对分类整数标签进行编码
from keras.utils import to_categorical
num_classes = 10
# 打印前十个(整数值)训练标签
print('Integer-valued labels:')
print(y_train[:10])
# 对标签进行一次性编码
# 将类别向量转换为二进制类别矩阵
y_train = to_categorical(y_train, num_classes)
y_test = to_categorical(y_test, num_classes)
# 打印前十个(单次)训练标签
print('One-hot labels:')
print(y_train[:10])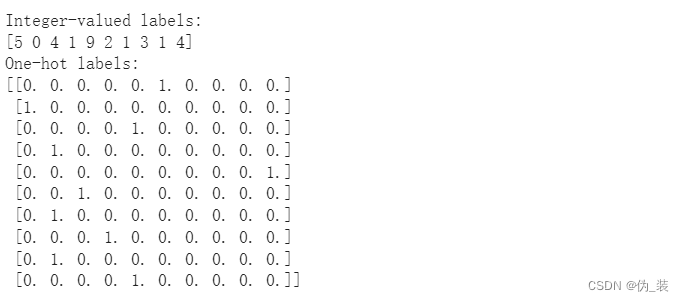 重塑数据以适应我们的 CNN(和 input_shape)
重塑数据以适应我们的 CNN(和 input_shape)
# 输入图像尺寸为 28x28 像素的图像。
img_rows, img_cols = 28, 28
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
print('input_shape: ', input_shape)
print('x_train shape:', X_train.shape)
定义模型架构
- strides – 卷积的步长。如果不指定任何参数,strides 将设为 1。
- padding – “有效 “或 “相同 “之一。如果不做任何指定,padding 将设置为 “有效”。
- activation – 通常为 “relu“。如果不指定任何内容,则不会应用激活。我们强烈建议你为网络中的每个卷积层添加 ReLU 激活函数。
- 始终为 CNN 中的 Conv2D 层添加 ReLU 激活函数。除网络中的最后一层外,密集层也应具有 ReLU 激活函数。
- 在构建分类网络时,网络的最终层应是具有 softmax 激活函数的密集层。最终层的节点数应等于数据集中的类总数。
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout
# 创建模型对象
model = Sequential()
# CONV_1: 添加 CONV 层,采用 RELU 激活,深度 = 32 内核
model.add(Conv2D(32, kernel_size=(3, 3), padding='same',activation='relu',input_shape=(28,28,1)))
# POOL_1: 对图像进行下采样,选择最佳特征
model.add(MaxPooling2D(pool_size=(2, 2)))
# CONV_2: 在这里,我们将深度增加到 64
model.add(Conv2D(64, (3, 3),padding='same', activation='relu'))
# POOL_2: more downsampling
model.add(MaxPooling2D(pool_size=(2, 2)))
# 由于维度过多,我们只需要一个分类输出
model.add(Flatten())
# FC_1: 完全连接,获取所有相关数据
model.add(Dense(64, activation='relu'))
# FC_2: 输出软最大值,将矩阵压制成 10 个类别的输出概率
model.add(Dense(10, activation='softmax'))
model.summary()
需要注意的事项:
- 网络以两个卷积层的序列开始,然后是最大池化层。
- 最后一层为数据集中的每个对象类别设置了一个条目,并具有软最大激活函数,因此可以返回概率。
- Conv2D 深度从输入层的 1 增加到 32 到 64。
- 我们还想减少高度和宽度–这就是 maxpooling 的作用所在。请注意,在池化层之后,图像尺寸从 28 减小到 14。
- 可以看到,每个输出形状都用 None 代替了批量大小。这是为了便于在运行时更改批次大小。
- 最后,我们会添加一个或多个全连接层来确定图像中包含的对象。例如,如果在上一个最大池化层中发现了车轮,那么这个 FC 层将转换该信息,以更高的概率预测图像中出现了一辆汽车。如果图像中有眼睛、腿和尾巴,那么这可能意味着图像中有一只狗。
编译模型
# rmsprop 和自适应学习率 (adaDelta) 是梯度下降的流行形式,仅次于 adam 和 adagrad
# 因为我们有多个类别 (10)
# 编译模型
model.compile(loss='categorical_crossentropy', optimizer='rmsprop',
metrics=['accuracy'])训练模型
from keras.callbacks import ModelCheckpoint
# 训练模型
checkpointer = ModelCheckpoint(filepath='model.weights.best.hdf5', verbose=1,
save_best_only=True)
hist = model.fit(X_train, y_train, batch_size=32, epochs=20,
validation_data=(X_test, y_test), callbacks=[checkpointer],
verbose=2, shuffle=True) 在验证集上加载分类准确率最高的模型
在验证集上加载分类准确率最高的模型
# 加载能获得最佳验证精度的权重
model.load_weights('model.weights.best.hdf5')计算测试集的分类准确率
# 评估测试的准确性
score = model.evaluate(X_test, y_test, verbose=0)
accuracy = 100*score[1]
# 打印测试精度
print('Test accuracy: %.4f%%' % accuracy)![]()
评估模型
import matplotlib.pyplot as plt
f, ax = plt.subplots()
ax.plot([None] + hist.history['accuracy'], 'o-')
ax.plot([None] + hist.history['val_accuracy'], 'x-')
# 绘制图例并自动使用最佳位置: loc = 0。
ax.legend(['Train acc', 'Validation acc'], loc = 0)
ax.set_title('Training/Validation acc per Epoch')
ax.set_xlabel('Epoch')
ax.set_ylabel('acc')
plt.show()
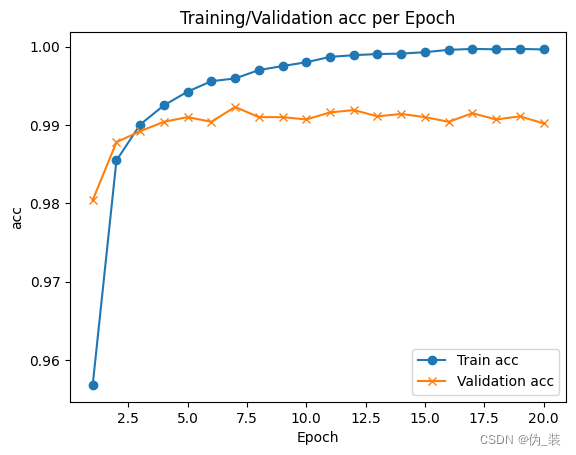
import matplotlib.pyplot as plt
f, ax = plt.subplots()
ax.plot([None] + hist.history['loss'], 'o-')
ax.plot([None] + hist.history['val_loss'], 'x-')
# Plot legend and use the best location automatically: loc = 0.
ax.legend(['Train loss', "Val loss"], loc = 0)
ax.set_title('Training/Validation Loss per Epoch')
ax.set_xlabel('Epoch')
ax.set_ylabel('Loss')
plt.show()
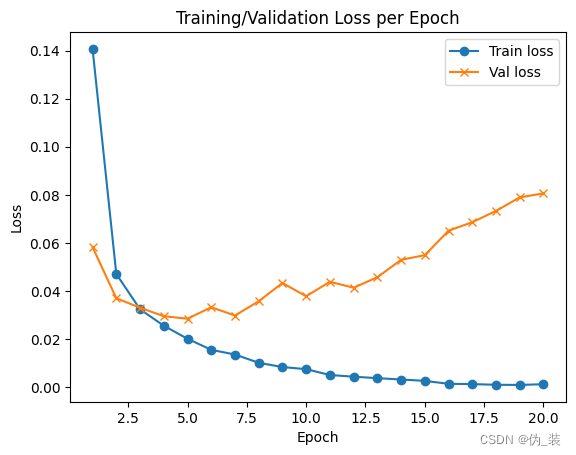
注意事项:
MLP 和 CNN 通常不会产生可比较的结果。MNIST 数据集非常特别,因为它非常干净,而且经过了完美的预处理。例如,所有图像大小相同,并以 28×28 像素网格为中心。如果数字稍有偏斜或不居中,这项任务就会难得多。对于真实世界中杂乱无章的图像数据,CNN 将真正超越 MLP。
为了直观地了解为什么会出现这种情况,要将图像输入 MLP,首先必须将图像转换为矢量。然后,MLP 会将图像视为没有特殊结构的简单数字向量。它不知道这些数字原本是按空间网格排列的。
相比之下,CNN 的设计目的完全相同,即处理多维数据中的模式。与 MLP 不同的是,CNN 知道,相距较近的图像像素比相距较远的像素关系密切。
原文地址:https://blog.csdn.net/weixin_62828995/article/details/134649278
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_39618.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。