pandas教程：Introduction to statsmodels statsmodels简介

13.3 Introduction to statsmodels（statsmodels简介）

statsmodels是一个有很多统计模型的python库，能完成很多统计测试，数据探索以及可视化。它也包含一些经典的统计方法，比如贝叶斯方法和一个机器学习的模型。

statsmodels中的模型包括：

• 线性模型（linear models），广义线性模型（generalized linear models），鲁棒线性模型（robust linear models）
• 线性混合效应模型（Linear mixed effects models）
• 方差分析(ANOVA)方法（Analysis of variance (ANOVA) methods）
• 时间序列处理（Time series processes）和状态空间模型（state space models）
• 广义矩估计方法（Generalized method of moments）

接下来我们用一些statsmodels中的工具，并了解如何使用Patsy公式和pandas DataFrame进行建模。

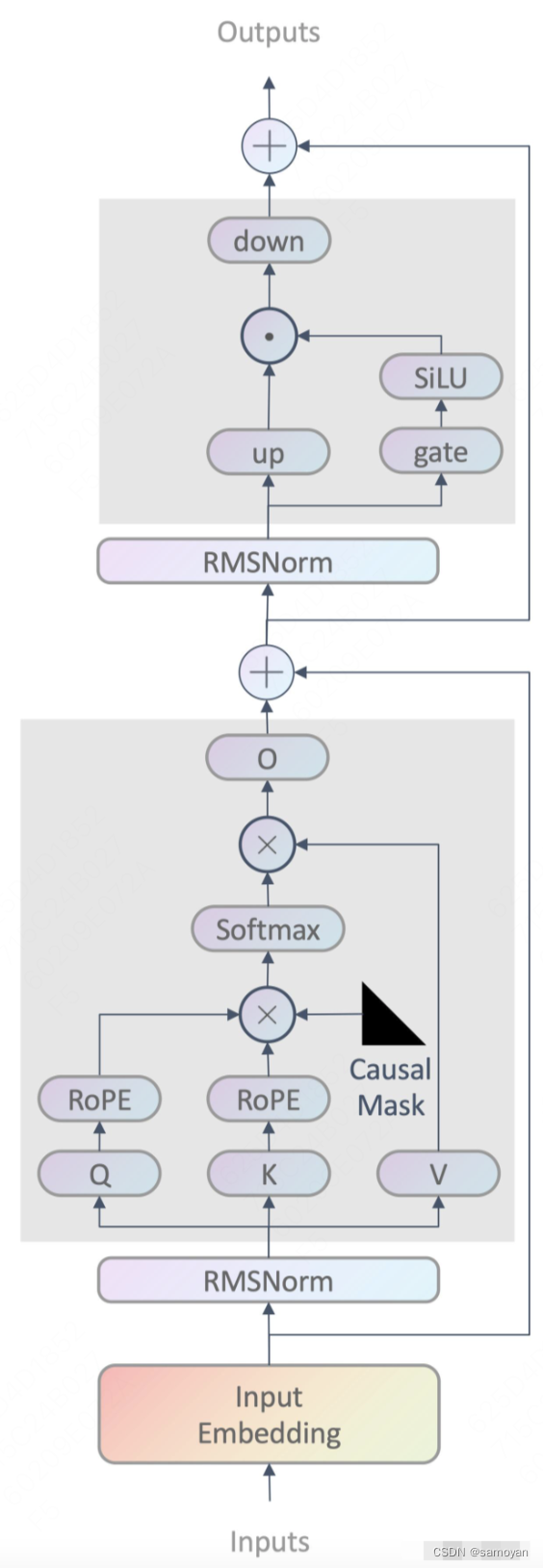
1 Estimating Linear Models（估计线性模型）

statsmodels中的线性模型大致分为两种：基于数组的（array-based），和基于公式的（formula-based）。调用的模块为：

import statsmodels.api as sm 
import statsmodels.formula.api as smf

为了演示如何使用，我们对一些随机数据生成一个线性模型：

import numpy as np
import pandas as pd

def dnorm(mean, variance, size=1):
    if isinstance(size, int):
        size = size
    return mean + np.sqrt(variance) * np.random.randn(size)
    
# For reproducibility 
np.random.seed(12345)

N = 100 
X = np.c_[dnorm(0, 0.4, size=N), 
          dnorm(0, 0.6, size=N), 
          dnorm(0, 0.2, size=N)] 

eps = dnorm(0, 0.1, size=N) 
beta = [0.1, 0.3, 0.5]

y = np.dot(X, beta) + eps

print(X.shape)
print(eps.shape)

(100, 3)
(100,)

真正的模型用的参数是beta，dnorm的功能是产生指定平均值和方差的随机离散数据，得到：

X[:5]

array([[-0.12946849, -1.21275292,  0.50422488],
       [ 0.30291036, -0.43574176, -0.25417986],
       [-0.32852189, -0.02530153,  0.13835097],
       [-0.35147471, -0.71960511, -0.25821463],
       [ 1.2432688 , -0.37379916, -0.52262905]])

y[:5]

array([ 0.42786349, -0.67348041, -0.09087764, -0.48949442, -0.12894109])

一个线性模型通常会有一个截距，这里我们用sm.add_constant函数添加一个截距列给X：

X_model = sm.add_constant(X)
X_model[:5]

array([[ 1.        , -0.12946849, -1.21275292,  0.50422488],
       [ 1.        ,  0.30291036, -0.43574176, -0.25417986],
       [ 1.        , -0.32852189, -0.02530153,  0.13835097],
       [ 1.        , -0.35147471, -0.71960511, -0.25821463],
       [ 1.        ,  1.2432688 , -0.37379916, -0.52262905]])

sm.OLS可以拟合（fit）普通最小二乘线性回归：

model = sm.OLS(y, X)

fit方法返回的是一个回顾结果对象，包含预测模型的参数和其他一些诊断数据：

results = model.fit()
results.params

array([ 0.17826108,  0.22303962,  0.50095093])

在results上调用summary方法，可能得到一些详细的诊断数据：

results.summary()

参数的名字通常为x1, x2，以此类推。假设所有的模型参数都在一个DataFrame里：

data = pd.DataFrame(X, columns=['col0', 'col1', 'col2'])
data['y'] = y

data.head()

现在我们可以使用statsmodels formula API（公式API）和Patsy的公式字符串：

results = smf.ols('y ~ col0 + col1 + col2', data=data).fit()
results.params

Intercept    0.033559
col0         0.176149
col1         0.224826
col2         0.514808
dtype: float64

results.tvalues

Intercept    0.952188
col0         3.319754
col1         4.850730
col2         6.303971
dtype: float64

可以看到statsmodel返回的结果是Series，而Series的索引部分是DataFrame的列名。当我们使用公式和pandas对象的时候，不需要使用add_constant。

如果得到新的数据，我们可以用预测模型的参数来进行预测：

results.predict(data[:5])

0   -0.002327
1   -0.141904
2    0.041226
3   -0.323070
4   -0.100535
dtype: float64

其他一些分析、诊断、可视化工具可以自己多尝试。

2 Estimating Time Series Processes（预测时序过程）

statsmodels中的另一个类是用于时间序列分析的，其中有自动回归处理（autoregressive processes）， 卡尔曼滤波（Kalman filtering），状态空间模型（state space models），多元回归模型（multivariate autoregressive models）。

让我们用自动回归结果和噪音模拟一个时间序列数据：

init_x = 4

import random
values = [init_x, init_x]
N = 1000

b0 = 0.8
b1 = -0.4
noise = dnorm(0, 0.1, N)
for i in range(N):
    new_x = values[-1] * b0 + values[-2] * b1 + noise[i]
    values.append(new_x)

values[:6]

[4,
 4,
 1.8977509636904242,
 0.086865262206104243,
 -0.57694691325353353,
 -0.49950238023089472]

这种数据有AR(2)结构（two lags，延迟两期），延迟参数是0.8和-0.4。当我们拟合一个AR模型，我们可能不知道延迟的期间是多少，所以可以在拟合时设一个比较大的延迟数字：

MAXLAGS = 5
model = sm.tsa.AR(values)
results = model.fit(MAXLAGS)

结果里的预测参数，第一个是解决，之后是两个延迟（lags）：

results.params

array([-0.00616093,  0.78446347, -0.40847891, -0.01364148,  0.01496872,
        0.01429462])

关于模型的更多细节，可以查看文档。

代码007普通

打赏 收藏 海报 链接