呀哈喽,我是结衣
不知不觉,我们的数据结构之路已经来到了,排序这个新的领域,虽然你会说我们还学过冒泡排序。但是冒泡排序的性能不高,今天我们要学习的希尔排序可就比冒泡快的多了。
希尔排序
希尔排序的前身是插入排序,可以说希尔排序就是插入排序的优化。并且优化了很多。所以在讲希尔排序前我们要先学会插入排序,不然在后续学习希尔排序会比较的吃力。那么让我们先进入插入排序的教学吧。
插入排序
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际上我们玩扑克的时候就运用了插入排序的思想
本来想放张插入排序动图的,可是放进来后它就不动了。。。
下面我们来讲解插入排序的特点:
void InsertSort(int* a, int n)
{
for(int i = 0;i<n-1;i++)
{
int end = i;
int tmp = a[end + 1];
while (end>=0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
a[end + 1] = tmp;
}
}
}
思路:
在待排序的元素中,假设前end个元素已有序,现将第end+1个元素插入到前面已经排好的序列中,使得前end个元素有序。按照此法对所有元素进行插入,直到整个序列有序。但我们并不能确定待排元素中究竟哪一部分是有序的,所以我们一开始只能认为第一个元素是有序的,依次将其后面的元素插入到这个有序序列中来,直到整个序列有序为止
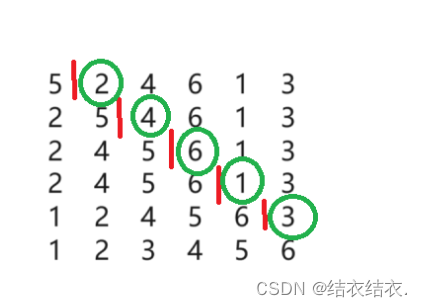
红色竖杆表示已经排好序列,绿色圈住的数字表示要插入到前面序列的数字。
希尔排序(缩小增量排序)
希尔排序的思想
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
在希尔排序中,我们要引入gap(间隔),我们来画图理解。
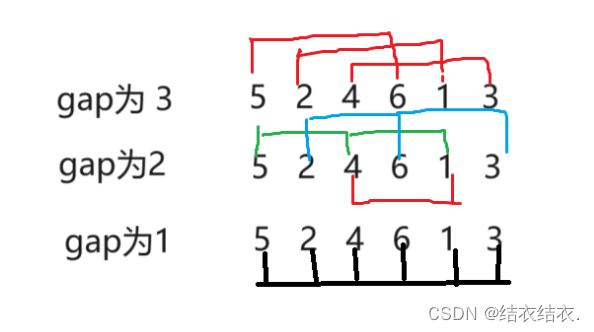
当gap不为1时,我们可以把它看做为一个预排序,先把数组变成比较有序。然后当gap为1时就是直接插入排序了,因为插入排序对比较有序的数组排列效率更高,所以希尔排序就为先预排序,再直接插入排序。
预排序
再讲希尔排序的代码实现前,我们先来讲预排序。我们先定义一个长度为6的逆序数组{6,5,4,3,2,1}.再来假设gap为3。
我们知道插入排序再排逆序的数组时时间复杂度为最坏的情况。所以我们才要进行预排序。

我们一组一组排

经过预排序后数组,已经变得比较有序了,这对后面的直接插入排序是有好处的,提高效率。
int gap = 3;
for(int i = 0;i<n-gap;i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
a[end + gap] = tmp;
}
}
这个只是一个预排序,和插入排序的思路大差不差,只是把改了一些细节。
看看打印结果

和我们前面推算的相同。
希尔排序的代码实现
思路讲完了,预排序也讲完了。希尔排序终于要来了。在现实情况下,我们能知道gap为多少吗?像前面我的只排6个数据,gap=3还是可以的,但是如果我们要排一百万,一千万,一亿甚至更多的数呢?gap又要怎么算呢?我们要知道。gap越小预排序越接近有序,但也排的越慢。gap越大,预排序越不接近有序,但排的越快。但是我们找不到gap应该取多少,所以我们可以让gap等于一个随机的数但要越来越小直到gap=1进行插入排序。
void ShellSort(int* a, int n)
{
int gap = n;
// gap > 1时是预排序,目的让他接近有序
// gap == 1是直接插入排序,目的是让他有序
while (gap>1)
{
gap = gap / 3 + 1;//也可以写成gap/2.目的都是为了最后一次gap一定要为1.
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
a[end + gap] = tmp;
}
}
}
}
可能写起来比较麻烦,都是希尔排序的效率可是非常高度。它的效率略低于但接近快排和堆排,远高于插入排序,插入排序的效率又远高于冒泡排序。希尔排序的时间复杂度在下方。
希尔排序的特性
原文地址:https://blog.csdn.net/2303_79015671/article/details/134796935
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_44868.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!