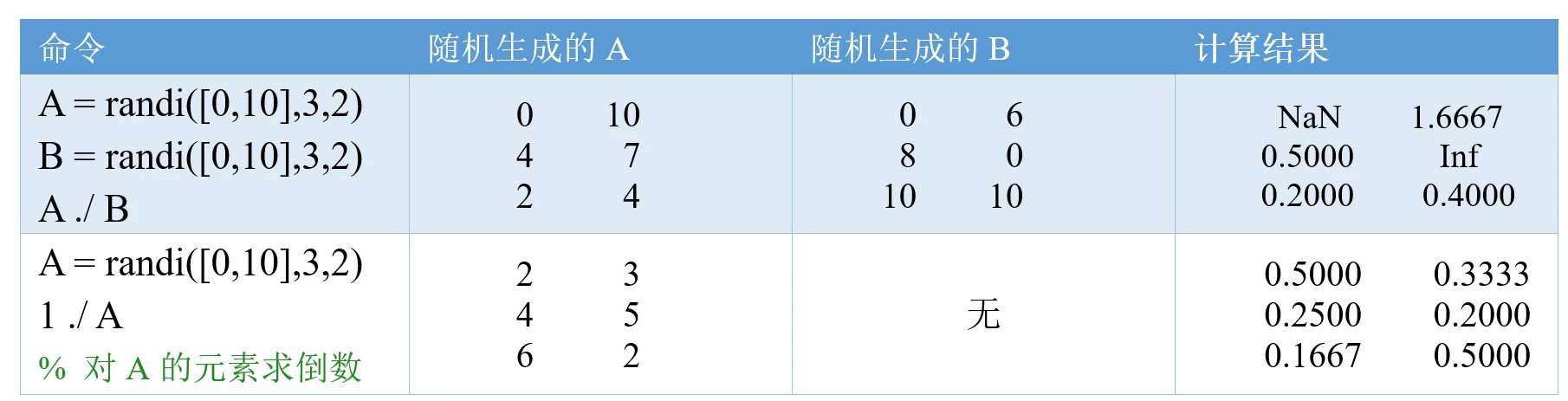
和矩阵函数不同的是,函数矩阵本质上是一个矩阵,是以函数作为元素的矩阵。
矩阵函数本质上是一个矩阵,是以矩阵作为自变量的函数。
函数矩阵和数字矩阵的运算法则完全相同。
不过矩阵的元素
j
(
)
[
,
]
可逆:
A
(
x
)
B
(
x
)
=
B
(
x
)
A
(
x
)
=
I
A(x)B(x)=B(x)A(x)=I
A(x)B(x)=B(x)A(x)=I
B
(
x
)
是
A
(
x
)
的逆矩阵
B(x)是A(x)的逆矩阵
B(x)是A(x)的逆矩阵,记为
A
−
1
(
x
)
A^{-1}(x)
A−1(x)
若
A
(
x
)
的元素
i
j
(
x
)
在
x
=
x
0
点均有极限
i
j
,
则
A
(
x
)
有极限
,
记为
l
i
x
→
x
0
A
(
x
)
=
A
(
x
0
)
。
若A(x)的元素a_{ij}(x)在x=x_0点均有极限 a_{ij}, \ 则A(x)有极限,记为underset{xrightarrow x_0}{lim}A(x)=A(x_0)。
若A(x)的元素aij(x)在x=x0点均有极限aij,则A(x)有极限,记为x→x0limA(x)=A(x0)。
则下面的等式成立
(
1
)
l
i
x
→
x
0
(
A
(
x
)
±
B
(
x
)
)
=
A
±
B
(
2
)
l
i
m
x
→
x
0
(
A
(
x
)
)
=
A
(
3
)
l
i
m
x
→
x
0
(
A
(
x
)
B
(
x
)
)
=
A
B
begin{align*} &(1)underset{xrightarrow x_0}{lim}(A(x)pm B(x))=Apm B\ &(2)underset{xrightarrow x_0}{lim}(kA(x))=kA \ &(3)underset{xrightarrow x_0}{lim}(A(x)B(x))=AB \ end{align*}
(1)x→x0lim(A(x)±B(x))=A±B(2)x→x0lim(kA(x))=kA(3)x→x0lim(A(x)B(x))=AB
看上去没有特别的地方,就是对每个元素进行求导积分即可。只是需要注意矩阵没有交换律。
线性向量微分方程
A
是一个
x
(
)
=
A
x
(
t
)
x
(
t
0
)
=
x
0
时,它的解为
x
=
A
(
t
−
t
0
)
x
0
A 是 一个 n 阶常数矩阵 ,则微分方程组\ {large frac{dx(t)}{dt}}=Ax(t)\ 满足初始条件为large x(t_0)=x_0时,它的解为\ large x=e^{A(t-t_0)}x_0\
A是一个n阶常数矩阵,则微分方程组dtdx(t)=Ax(t)满足初始条件为x(t0)=x0时,它的解为x=eA(t−t0)x0
定理二:
设
A
是一个
阶常数矩阵,则微分方程组
d
x
(
t
)
d
t
=
A
x
(
t
)
+
(
t
)
x
(
t
0
)
=
x
0
的解为
x
=
e
A
(
t
−
t
0
)
x
0
+
∫
t
0
t
e
A
(
t
−
τ
)
(
τ
)
d
τ
设A 是 一个 n 阶常数矩阵 ,则微分方程组\ {large frac{dx(t)}{dt}}=Ax(t) + f(t)\ 满足初始条件x(t_0)=x_0的解为\ large x=e^{A(t-t_0)}x_0+int_{t_0}^te^{A(t-tau)}f(tau)dtau
设A是一个n阶常数矩阵,则微分方程组dtdx(t)=Ax(t)+f(t)满足初始条件x(t0)=x0的解为x=eA(t−t0)x0+∫t0teA(t−τ)f(τ)dτ
(看着像高数里面的微分方程,但是又不太像。)
原文地址:https://blog.csdn.net/onlyyoujojo/article/details/134682791
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_45406.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!