冒泡排序、插入排序、选择排序这三种排序算法,它们的时间复杂度都是O(n^2),比较高,适合小规模数据的排序。如果数据量大,我们就需要使用到时间复杂度低的排序算法,归并排序和快速排序是复杂度为O(nlogn)的排序算法。
1-归并排序(Merge Sort)
如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。具体的流程如下:

从图中,我们看到归并排序实际是用到了分治的思想。将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
@Slf4j
public class MergeSort {
public static void main(String[] args) {
int []arr = {23,18,37,16,45,40,3,28,19};
sort(arr);
log.info("排序后的数组:arr={}",arr);
}
public static void sort(int []arr){
int []temp = new int[arr.length];//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
sort(arr,0,arr.length-1,temp);
}
private static void sort(int[] arr,int left,int right,int []temp){
if(left<right){
int mid = (left+right)/2;
sort(arr,left,mid,temp);//左边归并排序,使得左子序列有序
sort(arr,mid+1,right,temp);//右边归并排序,使得右子序列有序
merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
}
}
private static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;//左序列指针
int j = mid+1;//右序列指针
int t = 0;//临时数组指针
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while(j<=right){//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while(left <= right){
arr[left++] = temp[t++];
}
}
}
(1)归并排序是一个稳定的排序算法;
(2)最好情况、最坏情况,还是平均情况,时间复杂度都是O(nlogn);
(3)空间复杂度是O(n)。
2-快速排序
快速排序算法(Quicksort),我们习惯性把它简称为“快排”。快排利用的也是分治思想。快排的思想是这样的:如果要排序数组中下标从p到r之间的一组数据,我们选择p到r之间的任意一个数据作为pivot(分区点)。
下面的流程就是快排的一个轮回:
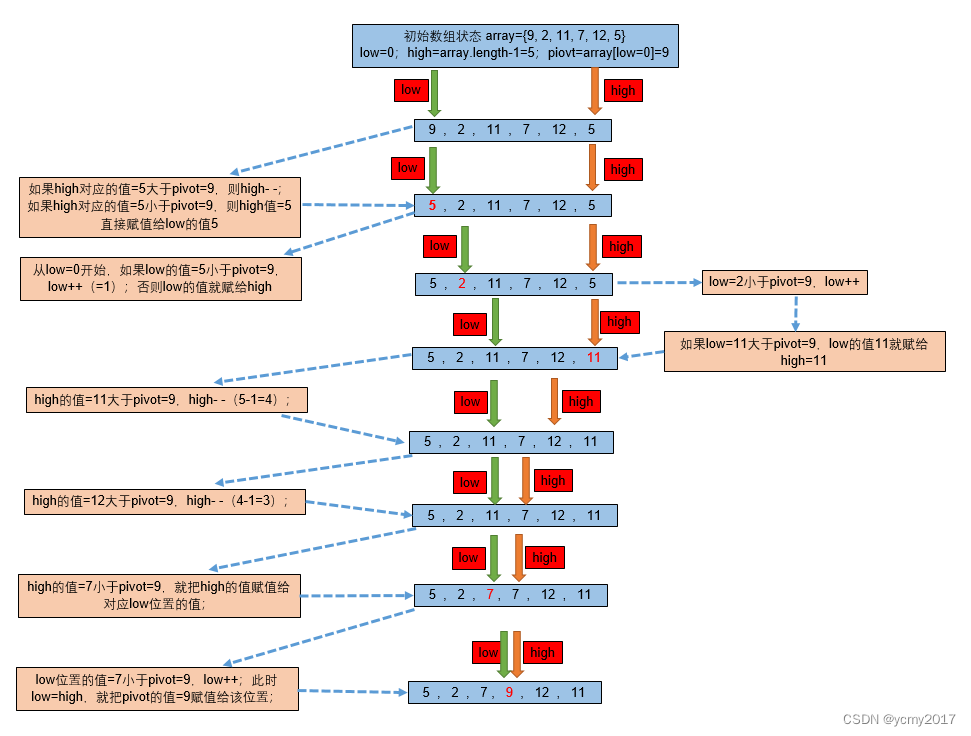
快速排序的代码实现:
@Slf4j
public class QuickSort2 {
public static void main(String[] args) {
//初始化需要排序的数组
int array[] = {9, 2, 11, 7, 12, 5};
//快速排序
quickSort(array, 0, array.length - 1);
//打印出排序好的序列
log.info("排序好的数组,array={}", array);
}
//快速排序
private static void quickSort(int[] array, int low, int high) {
if (low < high) {
//找到分区的位置,左边右边分别进行快速排序
int index = partition(array, low, high);
quickSort(array, 0, index - 1);
quickSort(array, index + 1, high);
}
}
//快速排序分区操作
private static int partition(int[] array, int low, int high) {
//选择基准
int pivot = array[low];
//当左指针小于右指针时,重复操作
while (low < high) {
while (low < high && array[high] >= pivot) {
high = high - 1;
}
array[low] = array[high];
while (low < high && array[low] <= pivot) {
low = low + 1;
}
array[high] = array[low];
}
//最后赋值基准
array[low] = pivot;
//返回基准所在位置,基准位置已经排序好
return low;
}
}
快排是一种原地、不稳定的排序算法。快排的平均时间复杂度是O(nlogn),最好的时间复杂度O(nlogn),最差的时间复杂度是O(n^2)。
原文地址:https://blog.csdn.net/ycmy2017/article/details/134807264
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_51189.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!