决策树–分类决策树

1、介绍

① 定义

分类决策树通过树形结构来模拟决策过程，决策树由结点和有向边组成。结点有两种类型：内部结

点和叶结点。内部结点表示一个特征或属性，叶子节点表示一个类。

② 生成过程

用决策树分类，从根结点开始，对样本的某一特征进行测试，根据测试结果，将样本分配到其他子

结点；这时，每一个子结点对应着该特征的一个取值，如此递归地对样本进行分配，直至达到叶结

点。最后将实例分到叶结点的类中。

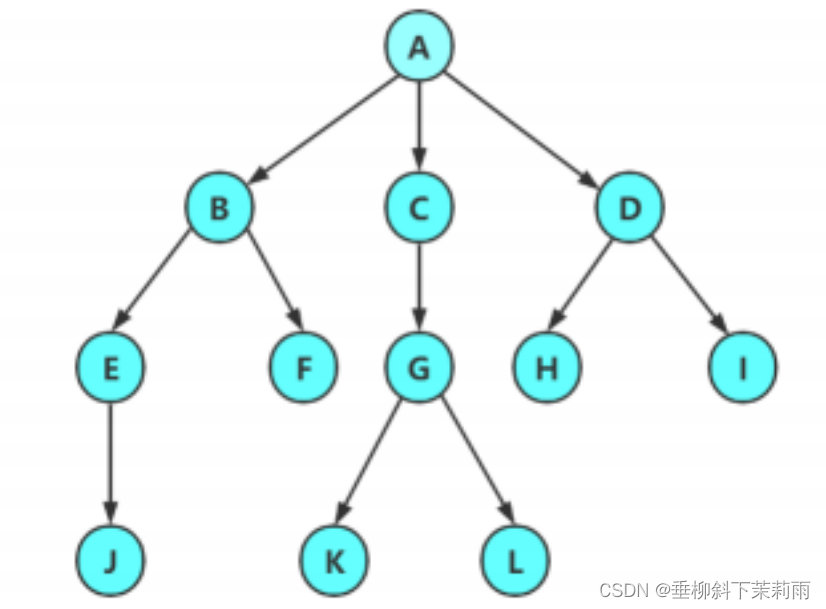
③ 示意图

​

2、特征选择–信息增益或信息增益比

（1）信息增益

① 熵的定义

信息增益是由熵构建而成，熵起源于热力学，后来由香农引用到信息论中，表示的是「随机变量的

不确定性」，不确定性越大，代表着熵越大。

由于熵和随机变量的分布有关，所以我们就可以写成：

② 信息增益算法

后者越小，说明对应的不确定性最小，意味着如果选择特征 A 为最优特征时，对于分的类是最为

确定的，对应的就希望这个信息增益是最大的。

③ 例题：对于上述表所给的训练数据集，根据信息增益准则选择最优特征。

​ ​

​

④ 缺点：如果不同特征内的分类个数不同，那么取值个数较多的特征计算出的信息增益会更大。因此，信息增益会更倾向于取值较多的特征。

（2）信息增益比

使用信息增益来作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。使用信息增

益比可以对这一问题进行校正，这是特征选择的另一准则。

代码007普通

打赏 收藏 海报 链接