C++高精度问题

高精度前言

C++中int不能超过2^31-1，最长的long long也不能超过2^63-1,所以我们在题目中如果碰到了很长很长的数，并且需要进行大数运算时，就需要高精度存储。

高精度总体思路

由于int和long long的限制，我们要想存放很长的数就需要利用数组存储,C++中可以利用STL中的vector容器存储

读取： 由于数据很大，用int存放不下，一般利用字符串读取

数据存放：用vector倒序存储，即将小位放到前面，将大位放到后面,这样方便数据处理

高精度算法

高精度加法

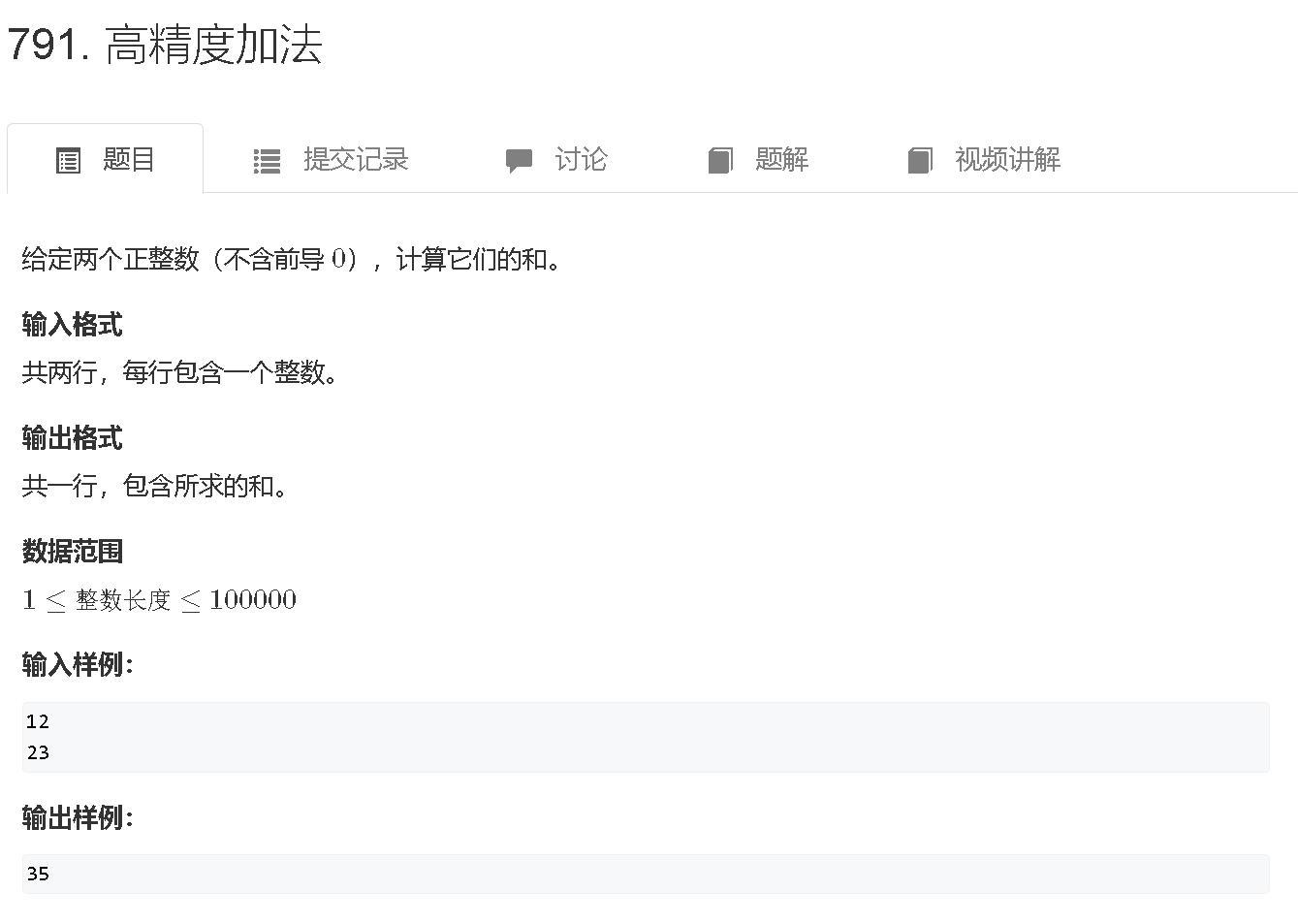
示例题目：

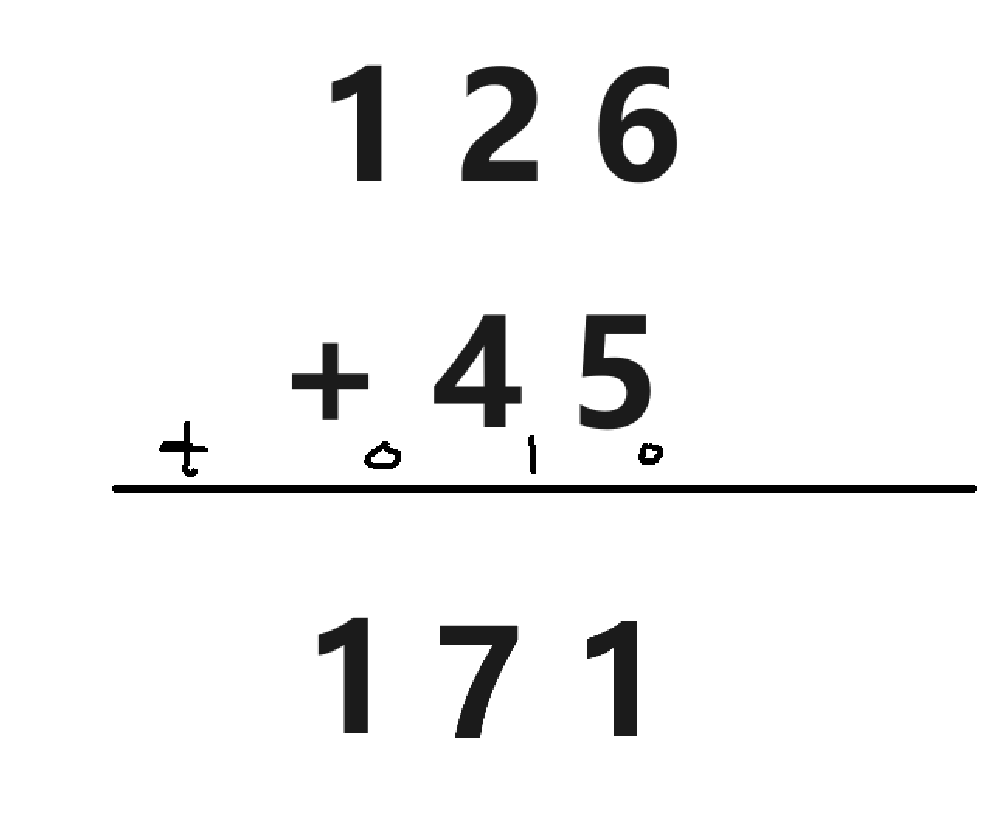
我们一般习惯是加法从个位数开始运算， t表示进位，初始t为0。先将个位数相加，图中为6+5=11

在加法中11%10 = 1为个位，11/10=1为进位，即t = 1，所以十位数相加为2+4+1=7，如此往复。根据此思路即可写出代码

//高精度加法
#include<iostream>
using namespace std;
#include<vector>

vector<int> add(vector<int> A,vector<int> B)
{
    //进位t初始为0
    int t = 0;
    vector<int> C;
    //i到任意一方结尾停止
    for(int i = 0;i<A.size() || i< B.size();i++)
    {
        if(i<A.size() ) t+=A[i];
        if(i< B.size()) t+=B[i];
        //相加后如果大于10要取余作为个位，如果小于10不影响
        C.push_back(t%10);
        //算进位
        t = t/10;
    }
    //最后一次计算 如果t为1 要在最高位补1
    if(t) C.push_back(t);
    return C;
}

int main()
{
    vector<int> A,B;
    //利用字符串读取
    string a,b;
    cin>>a>>b;
    //将高位存放在后面，低位存放的前面
    for(int i = a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    for(int i = b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    //auto为自动判断类型，会自动判断函数的返回类型
    auto C = add(A,B);
    for(int i = C.size()-1;i>=0;i--) cout<<C[i];
}

其中a[i]-‘0’是将字符类型的数字转换为整型类型的数字

需要注意的是这段代码

if(t) C.push_back(t);

这为了解决50+50 = 100类似的情况，最后一次计算后如果t=1，则需要在最高位补1。

高精度减法

示例题目： 

减法计算思路与加法相似

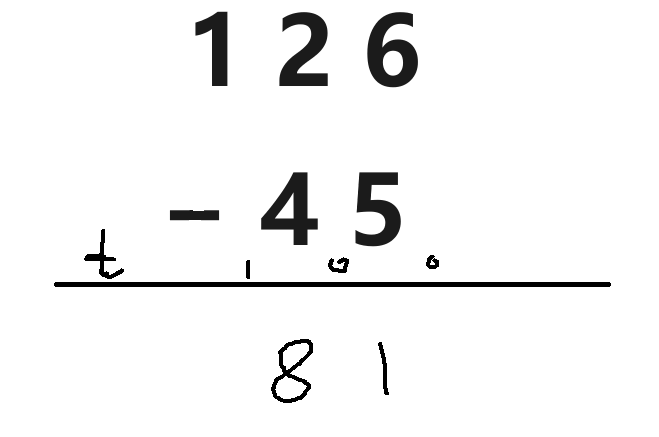
此时t表示的是借位，总体计算公式为 a[i]-b[i]-借位。

借位的计算

如果这次的A[i]-B[i] >= 0则下次的借位为0，反之下次计算的借位为1。

解决了计算的问题，减法还有负数的问题，如果小数减去大数要为负数，所以我们需要自己写一个判断两数大小的函数

bool cmp(vector<int>& A,vector<int>& B)
{
    if(A.size() != B.size()) return A.size()>B.size();
    for(int i =A.size()-1;i>=0;i--)
    {
        if(A[i] != B[i]) return A[i]>B[i];
    }
    return true;
}

先比较两数的位数，再依次比较两数的每一位，到最后还未得出结果，则返回true表示两数相等

在输出时分类讨论，负数先输出负号在输出数据即可

完整代码

//高精度减法模板
#include<iostream>
using namespace std;
#include<vector>
bool cmp(vector<int>& A,vector<int>& B)
{
    if(A.size() != B.size()) return A.size()>B.size();
    for(int i =A.size()-1;i>=0;i--)
    {
        if(A[i] != B[i]) return A[i]>B[i];
    }
    return true;
}


vector<int> sub(vector<int>& A,vector<int>& B)
{
    vector<int> C;
    for(int i=0,t=0;i<A.size();i++)
    {
        t = A[i] -t;
        if(i<B.size()) t-=B[i];
        C.push_back((t+10)%10);
        if(t<0) t=1;
        else t=0;
    }
    //去除前导0
    while(C.size()>1 && C.back() ==0  ) C.pop_back();
    return C;
}

int main()
{
    string a,b;
    vector<int> A,B;
    cin>>a>>b;
    for(int i = a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    for(int i = b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    //正数
    if(cmp(A,B))
    {
        auto C = sub(A,B);
        for(int i = C.size()-1;i>=0;i--) cout<<C[i];
    }
    //负数
    else
    {
        auto C = sub(B,A);
        cout<<"-";
        for(int i = C.size()-1;i>=0;i--) cout<<C[i];
    }


    return 0;
}

在题目中可能会出现需要去除前导0的情况

例如输出023,这个0没有实际意义,需要去除，被称为前导0

利用下面这段代码即可去除前导0

while(C.size()>1 && C.back() ==0  ) C.pop_back();

高精度乘法

示例题目：

高精度乘法一般只考虑大数乘以小数

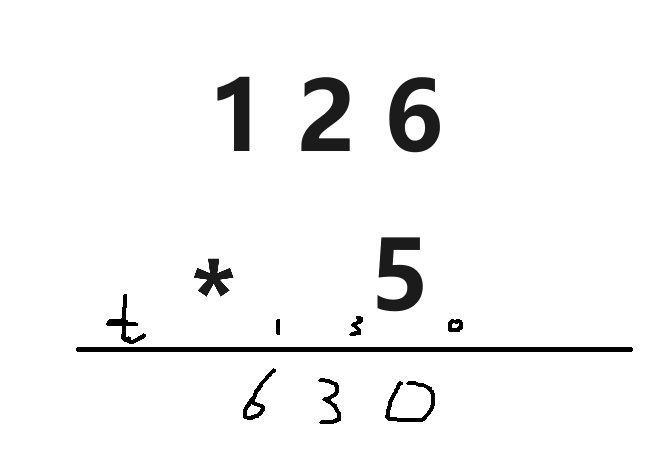
与加法十分类似，所以具体思路参考加法，需要注意的是，乘法也需要去前导0.

#include<iostream>
using namespace std;
#include<vector>

vector<int> mul(vector<int> A,int b)
{
    vector<int> C;
    int t = 0;
    for(int i = 0;i<A.size();i++) 
    {
        if(i<A.size()) t += A[i]*b;
        C.push_back(t%10);
        t = t/10;
    }
    while(C.size() >1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    string a;
    int b;
    vector<int> A;
    cin>>a>>b;
    for(int i = a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    auto C = mul(A,b);
    for(int i = C.size()-1;i>=0;i--) cout<<C[i];
    return 0;
}

高精度除法

实例题目

高精度除法需要注意的是余数，并且与加减乘法不同的是，除法是从高位开始计算的，而加减乘法是从低位开始计算的，需要加以区别

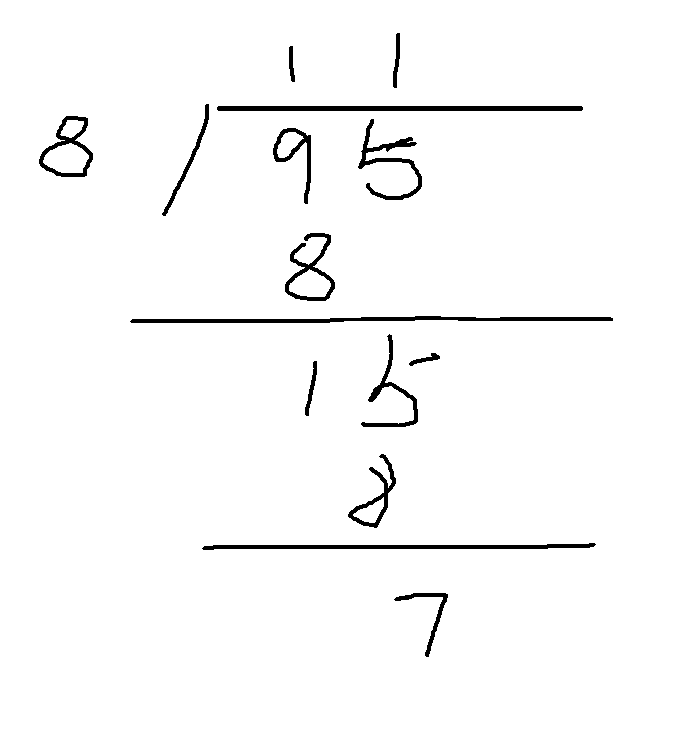
模拟除法过程我们可以发现，每次的被除数是上次计算得到的余数r*10加上a[i]，在图中为

1*10+5=15，我们将r/b入数组即可。

完整代码

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>

vector<int> div(vector<int>& A,int b,int& r)//r传入r的地址，便于直接对余数r进行修改
{
    r = 0;
    vector<int> C;
    for(int i = A.size()-1;i>=0;i--)//对A从最高位开始处理
    {
        r = r*10+A[i];//对A从最高位开始处理
        C.push_back(r/b);//将上次的余数*10在加上当前位的数字，便是该位需要除的被除数
        r = r%b;//余数
    }
    //由于在除法运算中，高位到低位运算，因此C的前导零都在vector的前面而不是尾部，vector只有删除最后一个数字pop_back是常数复杂度，而对于删除第一位没有相应的库函数可以使用，而且删除第一位，其余位也要前移，
    //因此我们将C翻转，这样0就位于数组尾部，可以使用pop函数删除前导0
    reverse(C.begin(),C.end());
    while(C.size()>1 && C.back() ==0 ) C.pop_back();
    return C;
}
int main()
{
    string a;
    int b;
    cin>>a>>b;
    vector<int> A;
    for(int i =a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    int r;
    auto C = div(A,b,r);
    for(int i = C.size()-1;i>=0;i--) cout<<C[i];
    cout<<endl<<r<<endl;
}

高精度除法同样需要去除前导0，不过不同的是，由于在除法运算中，高位到低位运算，因此C的前导零都在vector的前面而不是尾部，vector只有删除最后一个数字pop_back是常数复杂度，而对于删除第一位没有相应的库函数可以使用，而且删除第一位，其余位也要前移，因此我们可以利用reverse()函数将C翻转，这样0就位于数组尾部，可以使用pop函数删除前导0

此篇为学习之余的总结，作为笔记使用，如果有错误还请指正，谢谢！

代码007普通

打赏 收藏 海报 链接