Description
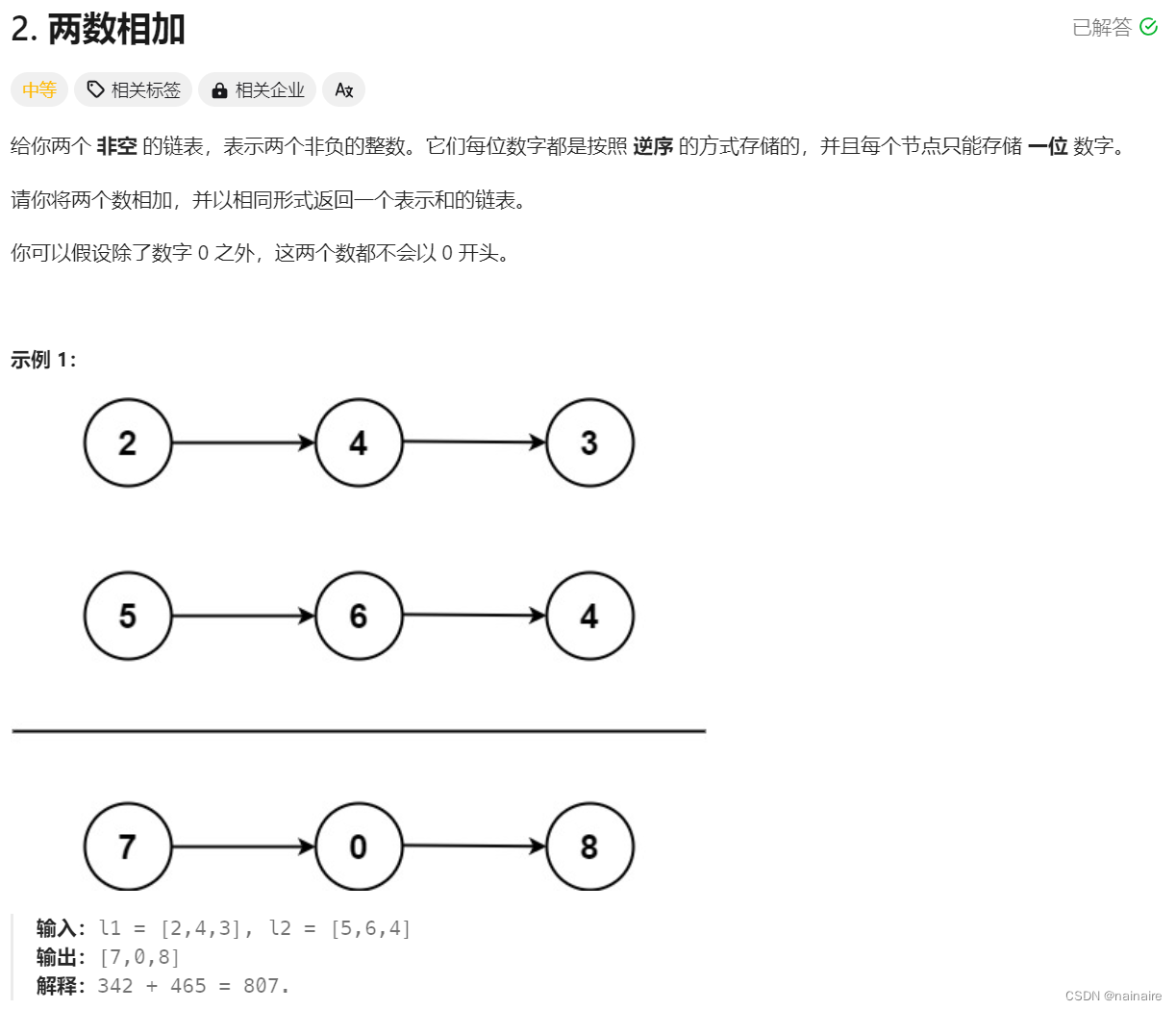
There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.
Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 10^9 + 7.
Example 1:
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output: 6
Example 2:
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output: 12
Constraints:
1 <= m, n <= 50
0 <= maxMove <= 50
0 <= startRow < m
0 <= startColumn < n
Solution
Solved after help…
Recursive, the function is f(x, y, step), and when x, y is out of boundary, return 1. If used up the step, return 0.
Time complexity:
o
(
m
∗
n
∗
m
a
x
M
o
v
e
)
o(m*n*maxMove)
o(m∗n∗maxMove)
Space complexity:
o
(
m
∗
n
∗
m
a
x
M
o
v
e
)
o(m*n*maxMove)
o(m∗n∗maxMove)
Code
class Solution:
def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
memo = {}
mod_val = 1000000007
def helper(x: int, y: int, step: int) -> int:
if x < 0 or x >= m or y < 0 or y >= n:
memo[(x, y, step)] = 1
return memo[(x, y, step)]
if step >= maxMove:
memo[(x, y, step)] = 0
return memo[(x, y, step)]
if (x, y, step) in memo:
return memo[(x, y, step)]
res = 0
for dz in (-1, 1):
res += helper(x + dz, y, step + 1)
res += helper(x, y + dz, step + 1)
memo[(x, y, step)] = res % mod_val
return memo[(x, y, step)]
return helper(startRow, startColumn, 0)
原文地址:https://blog.csdn.net/sinat_41679123/article/details/135858226
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.7code.cn/show_63189.html
如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！
