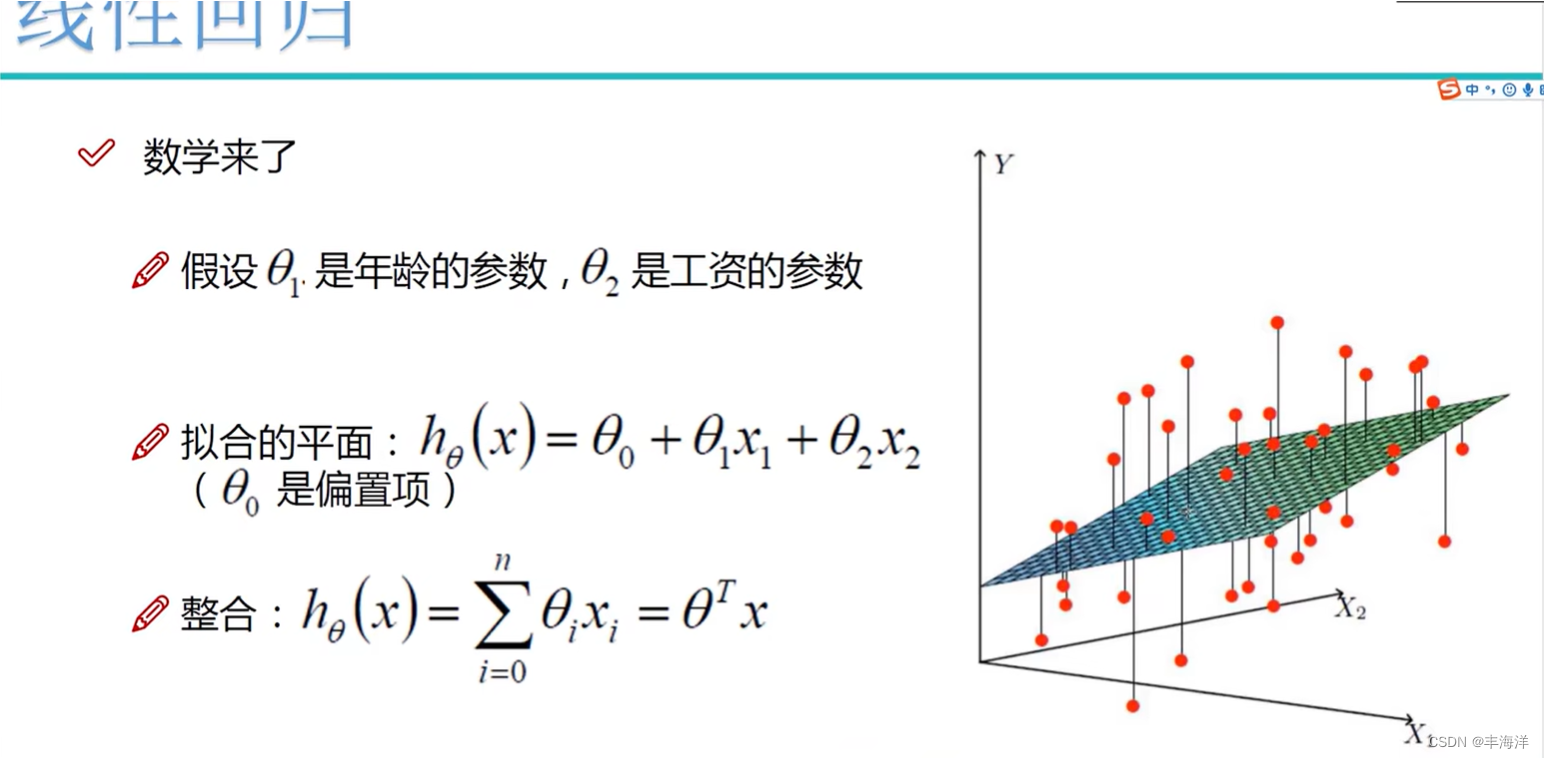
1和
2是权重项,
0是偏置项,在训练过程中为了使得训练结果更加精确而做的微调,不是一个大范围的因素,核心影响因素是权重项
为了完成矩阵的运算,在
0后面乘x0,使得满足矩阵的转换,所以在处理数据时候会添加如有上图所示的x0一列全是1的数据
为了得出这个平面,我们要做的就是找出所有的未知量
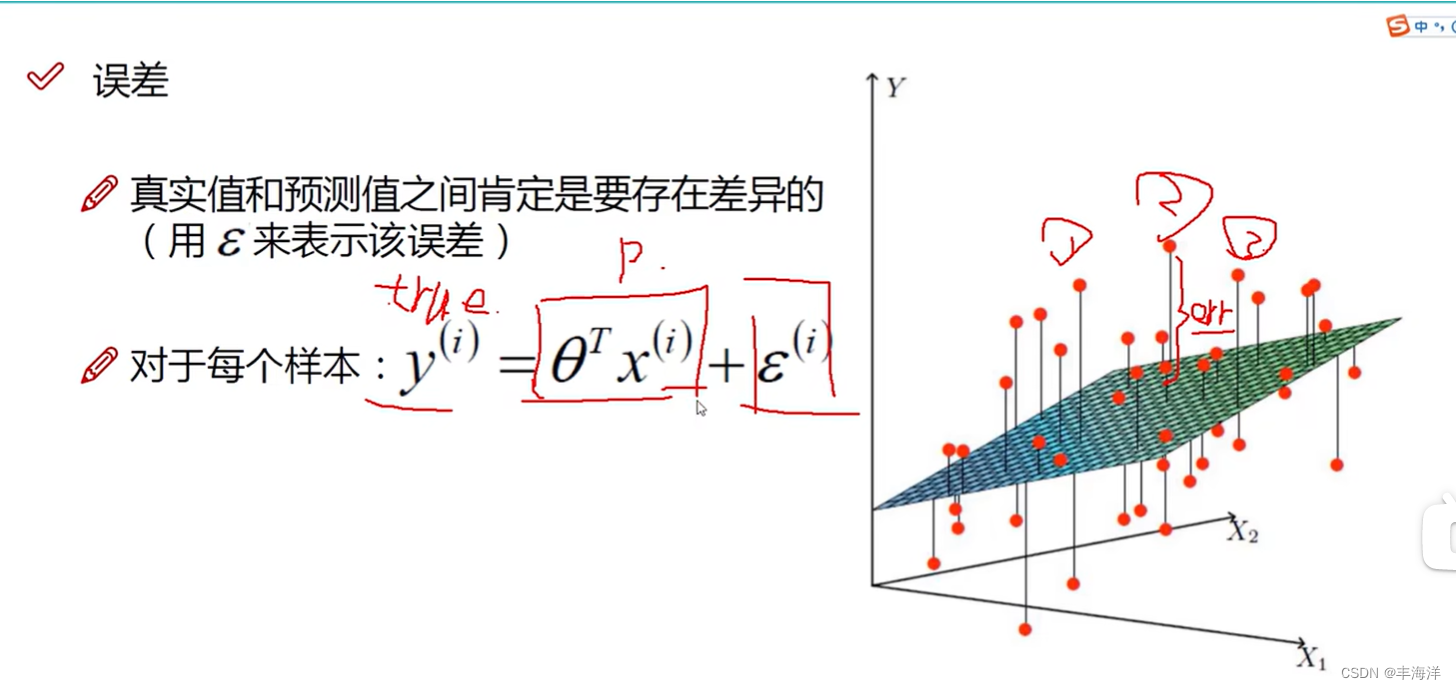
- y为真实值,
乘x是预测值,
是误差值,每个样本的真实值和误差值都存在误差
- 什么是机器学习呢:就是你给机器一堆数据,机器通过数据不断学习,调整参数,最终得出完美符合数据特征的参数,机器学习==调参侠
- 我们要想求斯塔,就要将关于
的算式转化成关于斯塔的算式
上图第三个算式左边的解释:x与组合后与y的数值越相近越好
为什么是累乘?因为需要大量的数据去完善最后的参数,使得参数更加准确,因为乘法难解,所以可以加上对数转换成加法,而且转换后虽然L的数值改变了,但是我们要求取的是
为何值使得L最大,所以不改变最后的
数值
要让似然函数数值最大化,由于前面的项是一个常数项,所以后面的项就要最小化
这里的x和
不是一个数,而是一个矩阵
经过求偏导,得出
,但是机器学习是一个通过不断学习的过程不断完善
这个参数,但是上面求解决
的过程并没有一个学习的过程
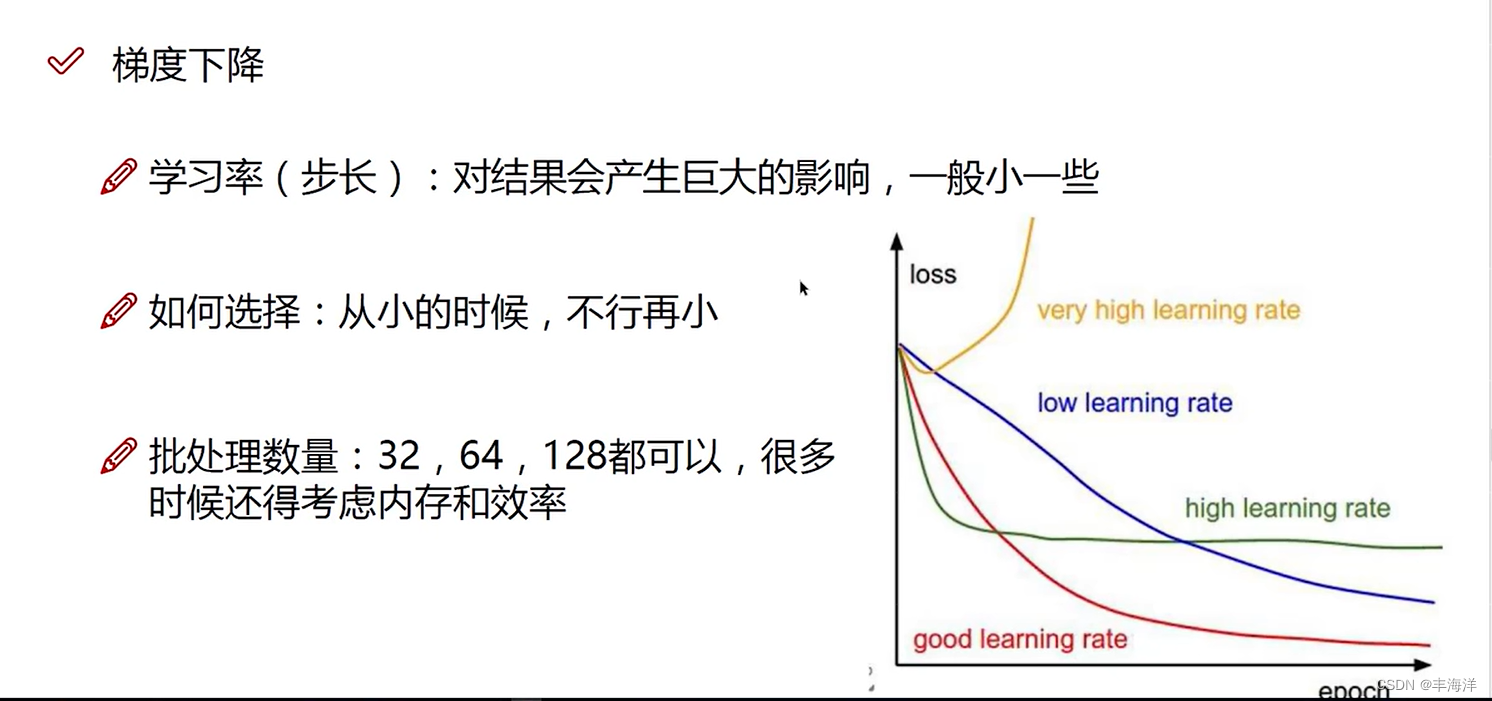
做切线,走一小步,然后继续做切线,继续一小步,直到走到最低点
有一个问题:计算
1和
0的时候是一起计算好还是分别单独计算好呢?答案是分别计算,因为参数具有独立性
第二个问题:如何找到当前最合适的方向,求偏导
解释一下这张图上的目标函数为什么多了个平方:是因为将数据的误差效果放大
这个公式就是对目标函数求偏导得出方向,因为梯度下降是沿这原来的反方向走,所以后面那个公式前面的符号改变成+号,表示在原来的初始位置
j的位置走那么长的距离
由于批量梯度下降和随机梯度下降各有各的毛病,所以一般采用小批量梯度下降法,每次更新选择一小部分数据来算,比较实用
批量梯度下降法公式中的α就是学习率
原文地址:https://blog.csdn.net/2301_79724443/article/details/135923157
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_64549.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!













![[技术杂谈]如何下载vscode历史版本](https://img-blog.csdnimg.cn/direct/18e927e78e82496e80649940eb70a716.png)