模糊神经网络控制器(MATLAB)

模糊神经网络控制器(Fuzzy Neural Network Controller)是将模糊控制和神经网络相结合的一类控制器。它综合了两者的优点,主要包括以下特点:

知识表达能力强。模糊系统的语言规则和神经网络的学习能力相结合,可以表示复杂的非线性映射关系。

自适应能力强。神经网络提供了在线学习和自适应的能力,可以根据过程的变化自动调整控制器的参数。

控制效果好。模糊推理结合神经网络近似能力,使控制效果优于传统PID控制器。

结构灵活。如T-S型、并行型等多种网络结构,可以根据实际需要选择。

模糊神经网络控制器的设计过程包括:确定输入输出变量、构建模糊控制规则、选择网络结构、确定学习算法以及仿真验证。应用领域十分广泛,如电机控制、机器人控制、化工过程控制等,特别适合对象复杂、模型难以建立的场合。

总体而言,模糊神经网络控制器集两种智能方法之长,是一种性能优异的现代控制策略。

MATLAB代码:

%% 模糊神经网络控制器主程序

% 清空MATLAB环境

clear all;%清除变量

close all;clc;%清空命令窗口

%% –(1)设置参数开始–

InputNumber = 2;%输入变量的数量

FuzzyPartitionNumber = 7;%模糊论域划分数量的设置

RuleNum = 49;%规则数量的设置

ProportionSum = 0;

[c1,b1,w1]=IniFuzzyNN(InputNumber,FuzzyPartitionNumber,RuleNum);%% 初始化模糊神经网络参数

x_input = [0;

    0]; % 神经网络输入初始化

myts=80e-6;%采样间隔

mynum=[500 1];%控制对象传递函数分子

myden=[10,20,5000];%控制对象传递函数分母

mysys=tf(mynum ,myden);

dsys=c2d(mysys,myts,’z’);%把传递函数转换为离散状态空间

[mynum myden] = tfdata(dsys,’v’);

N=5000;%采样点数

%输入信号为单位阶跃

rin=zeros(N,1);

for gen=1:1:N

    if gen>100

        rin(gen)=1.0;

    end

end

%模糊神经网络控制器的量化因子设置

Ke = 0.8;

Kec = 1e-4;

Ka = 3.5;%比例因子的设置

Kb = 6200;%积分因子的设置

%% 模糊神经网络控制器的控制量参数初始化

error_1 = rin(1);%误差初始化

%输出初始化

y_1=0;

y_2=0;

y_3=0;

%控制论初始化

u_1=0;

u_2=0;

u_3=0;

%% 模糊神经网络控制器的相关参数矩阵初始化

FuzzyBPnet=zeros(InputNumber,FuzzyPartitionNumber);

fuzzyData2=zeros(InputNumber,FuzzyPartitionNumber);

fuzzyData4=zeros(InputNumber,FuzzyPartitionNumber);

ecdata=zeros(N,1);

times=zeros(N,1);

yout=zeros(N,1);

errorData=zeros(N,1);

dError=zeros(N,1);

eData=zeros(N,1);

u=zeros(N,1);

for gen=1:1:N

    times(gen)=gen*myts;

    yout(gen)=-myden(2)*y_1-myden(3)*y_2+mynum(2)*u_1+mynum(3)*u_2;%二阶系统输出计算

    errorData(gen)=rin(gen)-yout(gen);%计算系统误差

    dError(gen) = (errorData(gen)-error_1)/myts;%系统误差变化

    eData(gen) = Ke*errorData(gen);%输入变量模糊化:液位差

    ecdata(gen) = Kec*dError(gen);%输入变量模糊化:液位差变化率

    %% 模糊控制输入变量范围限制

    % 液位差

    limite = 2;

    if eData(gen)>limite

        eData(gen)=limite;

    elseif eData(gen)<-limite

        eData(gen)=-limite;

    end

    % 液位差变化率

    limitec = 2;

    if ecdata(gen)>limitec

        ecdata(gen)=limitec;

    elseif ecdata(gen)<-limitec

        ecdata(gen)=-limitec;

    end

    %% 第1层输入层：模糊神经网络节点输入：液位差e,液位差变化率ec

    x_input(1) = eData(gen);

    x_input(2) = ecdata(gen);

    fuzzydata1 = x_input;

    %% 开始第2层模糊化层：进行模糊划分

    for i=1:1:InputNumber

        for j = 1:1:FuzzyPartitionNumber

            FuzzyBPnet(i,j) = -(fuzzydata1(i)-c1(i,j))^2/(2*b1(i,j)^2);

            fuzzyData2(i,j) = exp(FuzzyBPnet(i,j));

        end

    end

    for j = 1:1:FuzzyPartitionNumber% 提取模糊化层各节点的输出

        m1(j) = fuzzyData2(1,j);

        m2(j) = fuzzyData2(2,j);

    end

    %% 第3层推理层：模糊推理过程

    for i = 1:1:FuzzyPartitionNumber

        for j = 1:1:FuzzyPartitionNumber

            fuzzyData4(i,j) = m1(i)*m2(j);

        end

    end

    fuzzyData3 = [fuzzyData4(1,:),fuzzyData4(2,:),fuzzyData4(3,:),fuzzyData4(4,:),fuzzyData4(5,:),fuzzyData4(6,:),fuzzyData4(7,:)]; %对规则层各节点输出

    %% 第4层是归一化层：对变量进行归一化计算

    fall_sum = 0;

    for i = 1:1:RuleNum

        fall_sum = fall_sum+fuzzyData3(i);

    end

    % 归一化层节点输出

    f4 = fuzzyData3/fall_sum;

    NormalizationOutput(gen) = w1’*fuzzyData3′;

    %% 第5层输出层：对模糊控制输出进行清晰化

    ProportionSum = ProportionSum+NormalizationOutput(gen)*myts;

    u(gen) = Ka*NormalizationOutput (gen)+ Kb*ProportionSum ;

    %控制器的输出范围限制

    limitu=15.5;

    if u(gen)>limitu

        u(gen)=limitu;

    elseif u(gen)<-limitu

        u(gen)=-limitu;

    end

    %% 更新 输出量和控制量,注意是二阶系统

    u_3=u_2;

    u_2=u_1;

    u_1=u(gen);

    y_3=y_2;

    y_2=y_1;

    y_1=yout(gen);

    error_2 = error_1;

    error_1=errorData(gen);

end

%% 绘制仿真图

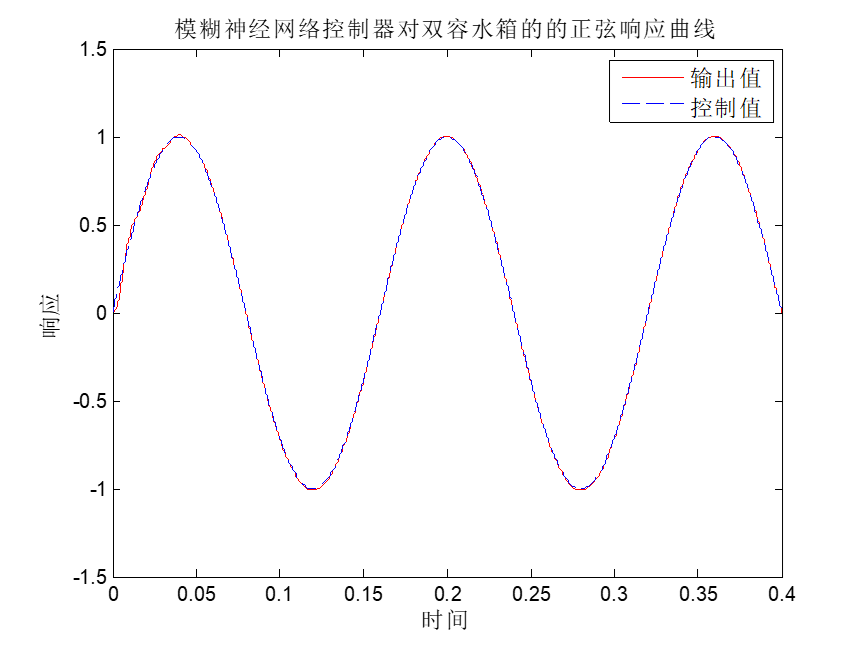
figure

plot(times,yout,’r’);

hold on;

plot(times,rin,’b’);

legend(‘输出值’,’控制值’);

xlabel(‘时间’);

ylabel(‘响应’);

title(‘模糊神经网络控制器对双容水箱的的阶跃相应曲线’);

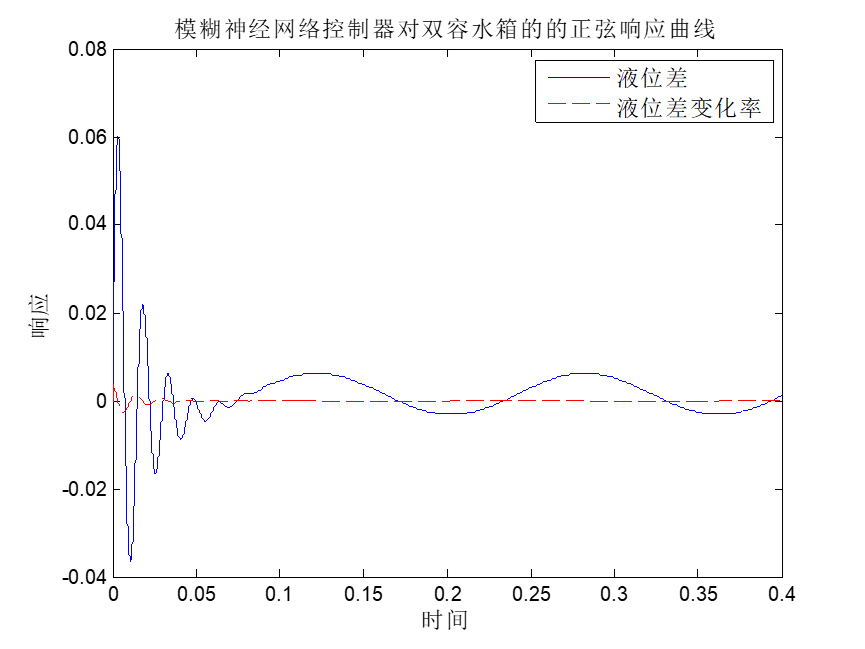
figure

plot(times,eData,’blue’,times,ecdata,’r’);

legend(‘e’,’ec’);

legend(‘液位差’,’液位差变化率’);

xlabel(‘时间’);

ylabel(‘响应’);

title(‘模糊神经网络控制器对双容水箱的的阶跃相应曲线’);

程序结果:

代码007普通

打赏 收藏 海报 链接