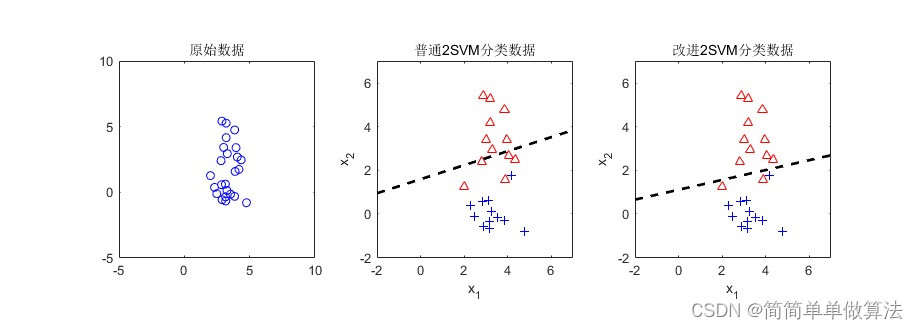
支持向量机(Support Vector Machines,SVM)是一种强大的监督学习模型,常用于分类、回归和异常值检测任务。它的核心思想是通过构建一个最大间隔超平面来有效地分隔不同类别的数据点。
在SVM中,数据点被视为p维向量,每个元素表示一个特征。目标是找到一个(p-1)维超平面,使得超平面与每个类别最近的数据点之间的间隔最大化。 这个间隔被称为边际,而具有最大边际的超平面被称为最大间隔超平面。最大间隔超平面的选择是通过解决一个优化问题来实现的,其中间隔损失函数和正则化项被最小化。
SVM不仅适用于线性可分的数据,还可以处理非线性可分的数据。对于非线性可分的情况,SVM使用了核技巧来将数据映射到高维特征空间。核函数是一种特殊的函数,它能够在高维空间中计算数据点之间的内积,而不需要显式地进行高维计算。通过使用核函数,SVM可以在高维空间中找到一个超平面,将数据点分隔开。常用的核函数包括线性核、多项式核和径向基函数(RBF)核等。
1. 收集和预处理数据: 收集具有已知类别标签的训练数据,并对数据进行预处理,例如特征缩放或去除噪声。
2. 选择合适的核函数: 根据数据的特性选择合适的核函数,以便在高维空间中进行准确的分类。
3. 定义优化目标: 构建一个目标函数,既考虑间隔损失又考虑正则化项,以平衡间隔最大化和模型复杂度。
4. 解决优化问题: 使用常用的优化算法(例如凸优化算法)求解目标函数,找到最优解。
5. 对新数据进行预测: 使用学习到的模型,对新的未知数据点进行预测,并划分到相应的类别中。
分类问题示例和代码请参见我的这篇文章:
SVMpython代码实现二分类问题
除了常规的分类问题,SVM还可以用于回归分析和异常值检测。在回归问题中,SVM尝试构建一个超平面,使得与该超平面距离最近的训练数据点的总和最小化。而在异常值检测中,SVM可以通过识别离超平面较远的数据点来检测潜在的异常值。
SVM作为一种强大的机器学习算法,在实际应用中具有广泛的应用。它的优点包括对线性和非线性可分数据的处理能力,以及对于高维数据集的适应性。然而,使用SVM时需要注意调整正则化参数和核函数等超参数,以避免过拟合和欠拟合。此外,对于大规模数据集,训练和推理过程可能需要较长的时间。
总而言之,支持向量机是一种强大且灵活的机器学习模型。它通过构建最大间隔超平面来实现数据分类和回归,并具有处理非线性可分数据的能力。SVM在实际应用中具有广泛的适用性,为解决各种复杂问题提供了一种可靠的工具。
如果你想更深入地了解人工智能的其他方面,比如机器学习、深度学习、自然语言处理等等,也可以点击这个链接,我按照如下图所示的学习路线为大家整理了100多G的学习资源,基本涵盖了人工智能学习的所有内容,包括了目前人工智能领域最新顶会论文合集和丰富详细的项目实战资料,可以帮助你入门和进阶。
人工智能交流群(大量资料)

原文地址:https://blog.csdn.net/m0_73916791/article/details/134677206
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_6807.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!