前言
本文主要是基于多元回归线性模型,然后建立模型和分析,解决多元线性回归模型存在的问题和优化多元线性回归模型,原理就不多讲了,可查看《应用回归分析》这本书,本文直接从例子讲解和分析,代码则是基于Python。
一、读取数据
首先是读取数据,观察数据是否有缺失和异常值,没有就可以直接进行建模,数据如下所示:
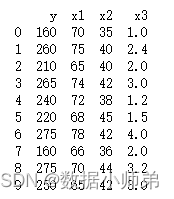
代码如下:
import pandas as pd
# Load data
#第一种方式,这种方式是你的文件夹有中文名的打开方式
f = open('文件路径', encoding='gbk')
df = pd.read_csv(f)
f.close()
print(df) #查看数据
#第二种方式是数据在全英的文件夹中的打开方式
df = pd.read_csv("文件路径")
print(df)二、建立模型
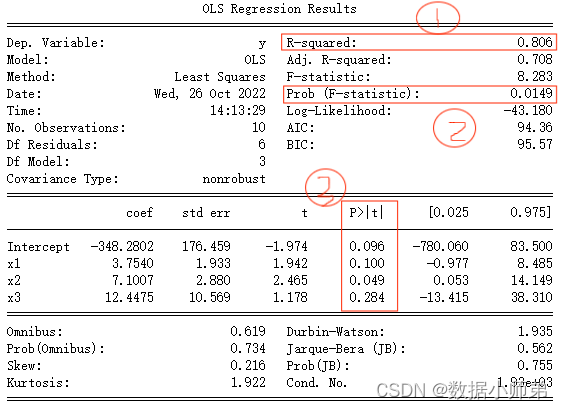
这个表格如何看呢?首先我们只要看我圈住的这三个地方就可以了,其他的主要用到的就是coef这列数据,这些数据是常数项和自变量的系数值。首先看第①个地方,这是模型的拟合效果,也就是R方的值;接着看第②个地方,这是整个模型的F检验;最后看第③个地方,这是每个对应值的T检验。从这三个地方去判断模型是否需要优化,可见在第三个地方中,有变量的T检验没通过,所以该模型还有待优化。
原理部分可以参考我的这篇文章,原理是一样的,只是变成了多个因变量 一元线性回归模型(保姆级)_数据小师弟的博客-CSDN博客_一元线性回归模型![]() https://blog.csdn.net/DL11007/article/details/126982286
https://blog.csdn.net/DL11007/article/details/126982286
代码如下:
import statsmodels.formula.api as smf
result = smf.ols('y~x1+x2+x3',data=df).fit()
print(result.params) # 自变量系数和常数项结果
print(result.summary()) # 模型拟合的结果:检验,R方等
print(result.pvalues) # 每个参数的P值三、预测新值

代码如下:
#单值
predictvalues = result.predict(pd.DataFrame({'x1': [75],'x2': [42],'x3':[1.6]}))
print(predictvalues)
#区间
predictions = result.get_prediction(pd.DataFrame({'x1': [75],'x2': [42],'x3':[1.6]}))
print(predictions.summary_frame(alpha=0.05))四、去截距模型

去截距建立的模型如上,可见R方有所提高,模型拟合效果提升。
代码如下:
result = smf.ols('y~x1+x2+x3-1',data=df).fit()
print(result.params) #自变量系数和常数项结果
print(result.summary()) #模型拟合的结果:检验,R方等
print(result.pvalues) #每个参数的P值对应的预测效果也是有所变化的,结果如下图:

代码如下:
#单值
predictvalues = result.predict(pd.DataFrame({'x1': [75],'x2': [42],'x3':[1.6]}))
print(predictvalues)
#区间
predictions = result.get_prediction(pd.DataFrame({'x1': [75],'x2': [42],'x3':[1.6]}))
print(predictions.summary_frame(alpha=0.05))完整代码如下:
import numpy as np
import statsmodels.formula.api as smf
import pandas as pd
# Load data
f = open('D:Word文档和Pdf应用回归作业zy3.11.csv',encoding='gbk')
df = pd.read_csv(f)
f.close()
print(df)
result = smf.ols('y~x1+x2+x3',data=df).fit()
print(result.params) #自变量系数和常数项结果
print(result.summary()) #模型拟合的结果:检验,R方等
print(result.pvalues) #每个参数的P值
#=========预测新值(原模型)======================================================
#单值
predictvalues = result.predict(pd.DataFrame({'x1': [75],'x2': [42],'x3':[1.6]}))
print(predictvalues)
#区间
predictions = result.get_prediction(pd.DataFrame({'x1': [75],'x2': [42],'x3':[1.6]}))
print(predictions.summary_frame(alpha=0.05))
#去截距模型
result = smf.ols('y~x1+x2+x3-1',data=df).fit()
print(result.params) #自变量系数和常数项结果
print(result.summary()) #模型拟合的结果:检验,R方等
print(result.pvalues) #每个参数的P值
#=========预测新值(去截距模型)======================================================
#单值
predictvalues = result.predict(pd.DataFrame({'x1': [75],'x2': [42],'x3':[1.6]}))
print(predictvalues)
#区间
predictions = result.get_prediction(pd.DataFrame({'x1': [75],'x2': [42],'x3':[1.6]}))
print(predictions.summary_frame(alpha=0.05))总结
以上便是本文的内容了,模型存在的问题和优化部分,我后续会发布新的文章,这里主要讲的是多元回归模型的一个整体的建模过程,我也是新手,有很多问题有待指出,有问题可以评论区交流交流啦!
原文地址:https://blog.csdn.net/DL11007/article/details/128524503
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_6929.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!