本文介绍: 当是间隔形式时桶底需重新计算(就是高度数组连续,但是实际摆放有间隔,因为咱们是根据数组进行操作,所以此时需要计算桶底长度)若有1 ,则其前后俩数进行判断,如果前后俩数差大于1(注意前一个数是负数的情况需进行判断),则加入比后一个数大1的数。本算法借鉴于力扣灵神思路,进行了整合及解释,更易懂,当然眼看千遍不如手敲一遍,建议大家可以手推一遍更易理解。先对数组排序,便于判断,由于要加入此时所缺最小正整数,1 为最小正整数。输入:nums = [3,4,-1,1]41. 缺失的第一个正数。欢迎大家评论区提问!
首先来个开胃小菜,41.缺少最小整数(难度:困难)真实感觉像是个简单级别
41. 缺失的第一个正数 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 示例 1: 输入:nums = [1,2,0] 输出:3 示例 2: 输入:nums = [3,4,-1,1] 输出:2 示例 3: 输入:nums = [7,8,9,11,12] 输出:1
题解:
先对数组排序,便于判断,由于要加入此时所缺最小正整数,1 为最小正整数 则先对数组判断,要是没有1 则直接返回要加入1 若有1 ,则其前后俩数进行判断,如果前后俩数差大于1(注意前一个数是负数的情况需进行判断),则加入比后一个数大1的数 否则此时数组相当于依次存储(差都为1,即无数可插)此时返回 插入最大值+1 注意:由于事先已进行排序,故不存在前后俩数之差小于 1 的情况
class Solution(object):
def firstMissingPositive(self, nums):
nums.sort()
if 1 not in nums:
return 1
for i in range(1, len(nums)):
if nums[i] - nums[i-1] > 1 and nums[i-1] > 0:
return nums[i-1] + 1
return max(nums) + 1重点!!!接雨水问题
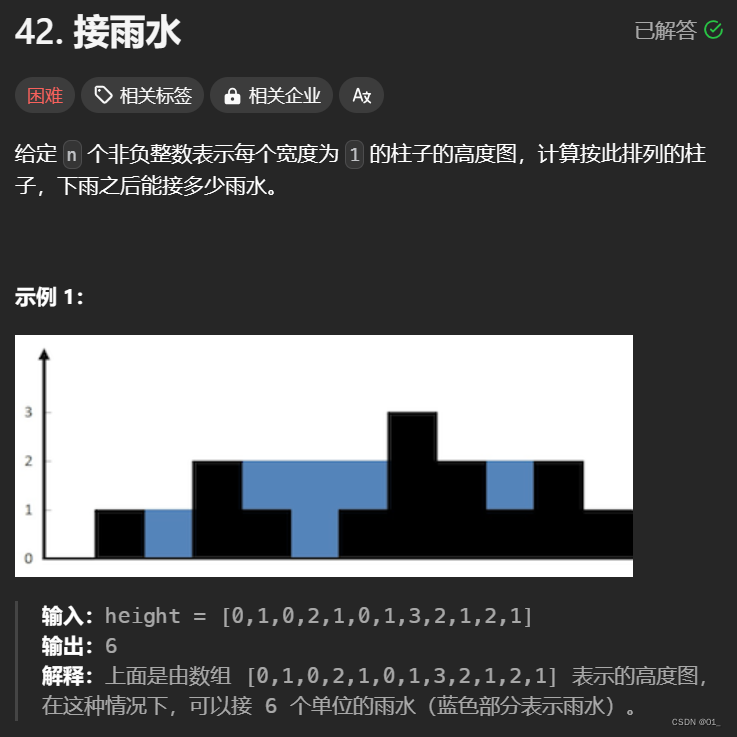
俩种解法;
前后缀方法 即计算出每个点的接水量
类似与短板水桶
|
| |
pre-> |__| <-sue
类似这样 前后缀相当于告诉以这个点为底他的筒壁高度,选取较小的
水量=筒壁高*底宽-底厚
因为咱们是一个点一个点计算,且题目告知高度是连续的,则桶底是1
水量=min(pre,sue)-h
注意:
当是间隔形式时桶底需重新计算
(就是高度数组连续,但是实际摆放有间隔,
因为咱们是根据数组进行操作,所以此时需要计算桶底长度)
注意:
当是间隔形式时桶底需重新计算(就是高度数组连续,但是实际摆放有间隔,因为咱们是根据数组进行操作,所以此时需要计算桶底长度)
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
res=0
# 保存前后缀的数组
pre=[0]*len(height)
sue=[0]*len(height)
# 第一个与最后一个没法比较需要申明
pre[0]=height[0]
sue[-1]=height[-1]
#记录前后缀
for i in range(1,len(height)):
pre[i]=max(height[i],pre[i-1])
for i in range(len(height)-2,-1,-1):
sue[i]=max(height[i],sue[i+1])
# 计算雨量
for i in range(len(height)):
res+=min(pre[i],sue[i])-height[i]
return res双指针指向头尾,计算前后缀,
如果前缀最大值小于后缀最大值则此时L指向的点的水量就可计算,同时指针右移
如果前缀最大值大于后缀最大值则此时r指向的点的水量就可计算,同时指针左移
可以结合上面的前后缀数组就可以看出来,前后缀的最大值会一直影响后面的前后缀
举例:
如果是前缀是1 后缀是2,因为前后缀每次都是选最大值值所以不管后继怎么变化,
现在l所指向的点最终肯定是前缀小于后缀的,故这时可以直接,按前缀数值进行计算水量class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
n=len(height)
# 定义双指针
l,r=0,n-1
pre_max,sue_max,res=0,0,0
while l<r:
# 计算前后缀最大值
pre_max=max(pre_max,height[l])
sue_max=max(sue_max,height[r])
# 进行判断,是否可以计算水量
if pre_max<sue_max:
res+=pre_max-height[l]
l+=1
elif pre_max>sue_max:
res+=sue_max-height[r]
r-=1
# 这一步else可写可不写,此时为相等的情况计算那一边都行,可以在上面俩个判断中任意一个加上相等判断
else:
res+=pre_max-height[l]
l+=1
return res这应该是暂时最优解,时间复杂度o(n) 空间复杂度o(1) 只有一些变量
本算法借鉴于力扣灵神思路,进行了整合及解释,更易懂,当然眼看千遍不如手敲一遍,建议大家可以手推一遍更易理解。
原文地址:https://blog.csdn.net/qq_46258829/article/details/134699058
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_8309.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。