本文介绍: 久违了,前段时间由于学习压力大,就没怎么更新MATLAB相关的内容,今天实在学不进去了,换个内容更新一下~本贴介绍灰色预测模型,这也是数学建模竞赛常见算法中的一员,和许多预测模型一样——根据已知数据对未知进行预测。
久违了,前段时间由于学习压力大,就没怎么更新MATLAB相关的内容,今天实在学不进去了,换个内容更新一下~
本贴介绍灰色预测模型,这也是数学建模竞赛常见算法中的一员,和许多预测模型一样——底层原理是根据已知数据对未知进行预测~
一.理论部分
灰色预测是对既含有已知信息又含有不确定信息的系统进行预测,就是对在一定范围内变化的、与时间有关的灰色过程进行预测。 灰色预测对原始数据进行生成处理来寻找系统变动的规律,并生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
二.例题讲解
如下是有关棉花生产的数据:
| 年份 | 单产 | 种子费 | 化肥费 | 农药费 | 机械费 | 灌溉费 |
| kg/公顷 | 元/公顷 | 元/公顷 | 元/公顷 | 元/公顷 | 元/公顷 | |
| 1990 | 1017 | 106.05 | 495.15 | 305.1 | 45.9 | 56.1 |
| 1991 | 1036.5 | 113.55 | 561.45 | 343.8 | 68.55 | 93.3 |
| 1992 | 792 | 104.55 | 584.85 | 414 | 73.2 | 104.55 |
| 1993 | 861 | 132.75 | 658.35 | 453.75 | 82.95 | 107.55 |
| 1994 | 901.5 | 174.3 | 904.05 | 625.05 | 114 | 152.1 |
| 1995 | 922.5 | 230.4 | 1248.75 | 834.45 | 143.85 | 176.4 |
| 1996 | 916.5 | 238.2 | 1361.55 | 720.75 | 165.15 | 194.25 |
| 1997 | 976.5 | 260.1 | 1337.4 | 727.65 | 201.9 | 291.75 |
| 1998 | 1024.5 | 270.6 | 1195.8 | 775.5 | 220.5 | 271.35 |
| 1999 | 1003.5 | 286.2 | 1171.8 | 610.95 | 195 | 284.55 |
| 2000 | 1069.5 | 282.9 | 1151.55 | 599.85 | 190.65 | 277.35 |
| 2001 | 1168.5 | 317.85 | 1105.8 | 553.8 | 211.05 | 290.1 |
| 2002 | 1228.5 | 319.65 | 1213.05 | 513.75 | 231.6 | 324.15 |
| 2003 | 1023 | 368.4 | 1274.1 | 567.45 | 239.85 | 331.8 |
| 2004 | 1144.5 | 466.2 | 1527.9 | 487.35 | 408 | 336.15 |
1.传统GM模型的代码
function [result, x0_hat, relative_residuals, eta] = gm11(x0, predict_num)
n = length(x0);
x1=cumsum(x0);
z1 = (x1(1:end-1) + x1(2:end)) / 2;
y = x0(2:end); x = z1;
k = ((n-1)*sum(x.*y)-sum(x)*sum(y))/((n-1)*sum(x.*x)-sum(x)*sum(x));
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/((n-1)*sum(x.*x)-sum(x)*sum(x));
a = -k;
x0_hat=zeros(n,1); x0_hat(1)=x0(1);
for m = 1: n-1
x0_hat(m+1) = (1-exp(a))*(x0(1)-b/a)*exp(-a*m);
end
result = zeros(predict_num,1);
for i = 1: predict_num
result(i) = (1-exp(a))*(x0(1)-b/a)*exp(-a*(n+i-1));
end
absolute_residuals = x0(2:end) - x0_hat(2:end);
relative_residuals = abs(absolute_residuals) ./ x0(2:end);
class_ratio = x0(2:end) ./ x0(1:end-1) ;
eta = abs(1-(1-0.5*a)/(1+0.5*a)*(1./class_ratio));
end2.原始数据检验
此处选用【单产】作为示例~
year =[1995:1:2001]'; % 横坐标表示年份,写成列向量的形式(加'就表示转置)
yield= [1017
1036.5
792
861
901.5
922.5
916.5
976.5
1024.5
1003.5
1069.5
1168.5
1228.5
1023
1144.5
]'; %原始数据序列,写成列向量的形式(加'就表示转置)ERROR = 0; % 建立一个错误指标,一旦出错就指定为1
% 判断是否有负数元素
if sum(yield<0) > 0
disp('灰色预测的时间序列中不能有负数!')
ERROR = 1;
end
% 判断数据量是否太少
n = length(yield); % 计算原始数据的长度
disp(strcat('原始数据的长度为',num2str(n)))
if n<=3
disp('数据量太小')
ERROR = 1;
end
% 数据太多时提示可考虑使用其他方法
if n>10
disp('考虑使用其他的方法')
end
% 判断数据是否为列向量,如果输入的是行向量则转置为列向量
if size(yield,1) == 1
yield = yield';
end
if size(year,1) == 1
year = year';
end3.准指数规律检验
if ERROR == 0
disp('准指数规律检验')
x1 = cumsum(yield);
rho = yield(2:end) ./ x1(1:end-1) ;
rho
figure(2)
plot(year(2:end),rho,'o-',[year(2),year(end)],[0.5,0.5],'-');
grid on;
text(year(end-1)+0.2,0.55,'临界线')
set(gca,'xtick',year(2:1:end))
xlabel('年份'); ylabel('原始数据的光滑度');
disp(strcat('指标1:光滑比小于0.5的数据占比为',num2str(100*sum(rho<0.5)/(n-1)),'%'))
disp(strcat('指标2:除去前两个时期外,光滑比小于0.5的数据占为',num2str(100*sum(rho(3:end)<0.5)/(n-3)),'%'))
disp('参考标准:指标1一般要大于60%, 指标2要大于90%!')
Judge = input('你认为可以通过准指数规律的检验吗?可以通过请输入1,不能请输入0:');
if Judge == 0
disp('灰色预测模型不适合你的数据!')
ERROR = 1;
end
end4.传统的GM(1,1)预测
if n > 7
test_num = 3;
else
test_num = 2;
end
train_yield = yield(1:end-test_num);
disp('训练数据是: ')
disp(mat2str(train_yield'))
test_yield = yield(end-test_num+1:end);
disp('试验数据是: ')
disp(mat2str(test_yield'))
disp(' ')
disp('***下面是传统的GM(1,1)模型预测的详细过程***')
result1 = gm11(train_yield, test_num);5.评估误差精度
%% 残差检验
average_relative_residuals = mean(relative_residuals);
disp(strcat('平均相对残差为',num2str(average_relative_residuals)))
if average_relative_residuals<0.1
disp('该模型对原数据的拟合程度非常不错!')
elseif average_relative_residuals<0.2
disp('该模型对原数据的拟合程度达到一般要求!')
else
disp('该模型对原数据的拟合程度不太好!')
end
%% 级比偏差检验
average_eta = mean(eta); % 计算平均级比偏差
disp(strcat('平均级比偏差为',num2str(average_eta)))
if average_eta<0.1
disp('该模型对原数据的拟合程度非常不错!')
elseif average_eta<0.2
disp('该模型对原数据的拟合程度达到一般要求!')
else
disp('该模型对原数据的拟合程度不太好!')
end
disp(' ')
答案如下,大家自己尝试(每个单独预测一遍,因为GM(1,1)只针对一维数据~)
| 年份 | 单产 | 种子费 | 化肥费 | 农药费 | 机械费 | 灌溉费 |
| kg/公顷 | 元/公顷 | 元/公顷 | 元/公顷 | 元/公顷 | 元/公顷 | |
| 2005 | 1122 | 449.85 | 1703.25 | 555.15 | 402.3 | 358.8 |
| 2006 | 1276.5 | 537 | 1888.5 | 637.2 | 480.75 | 428.4 |
| 2007 | 1233 | 565.5 | 2009.85 | 715.65 | 562.05 | 456.9 |
三.实战案例
1.2022年美赛C题
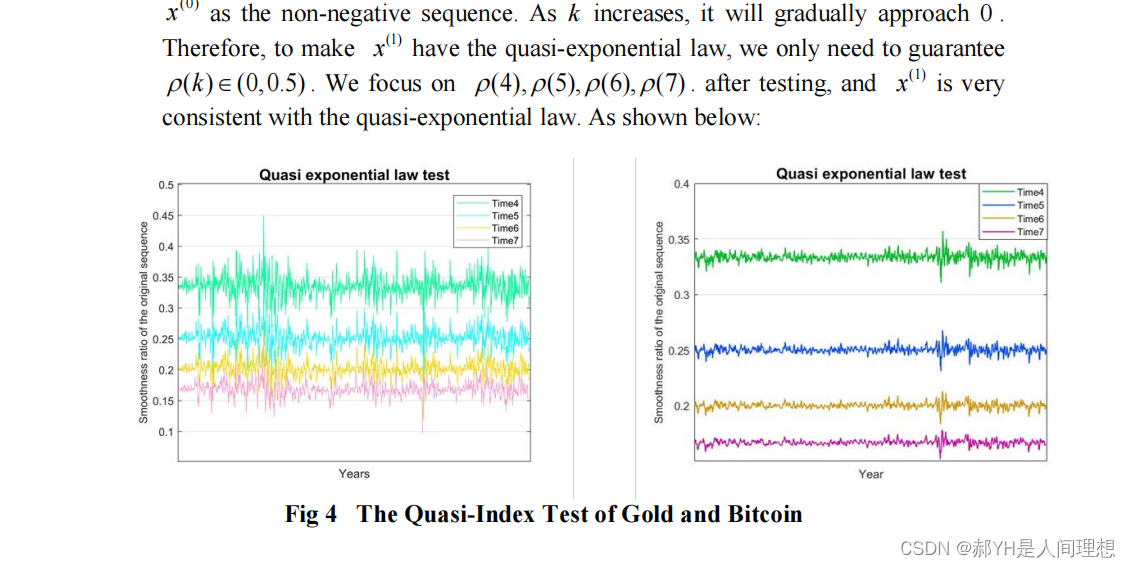
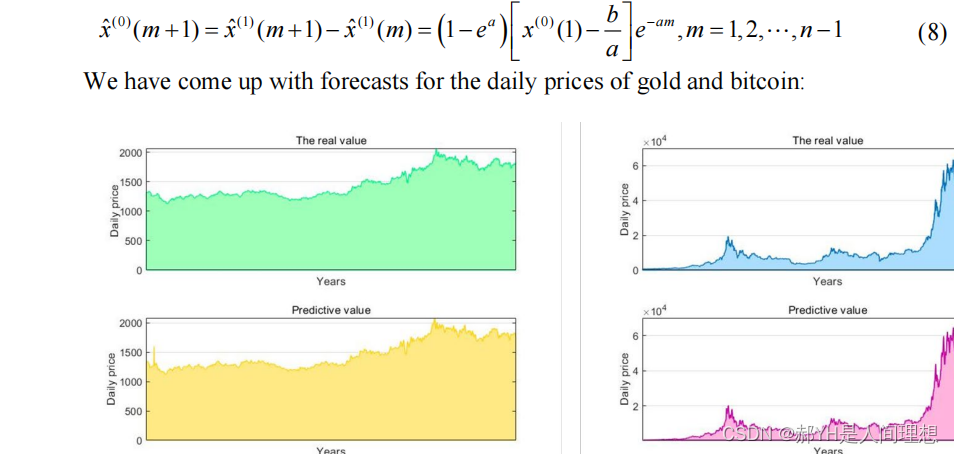

根据现有数据,通过灰色预测模型,预测比特币和黄金两种波动资产的走向,拟合优度较高,残差与级比偏差均很低,预测模型的可信度较高~
2.2022亚太赛C题
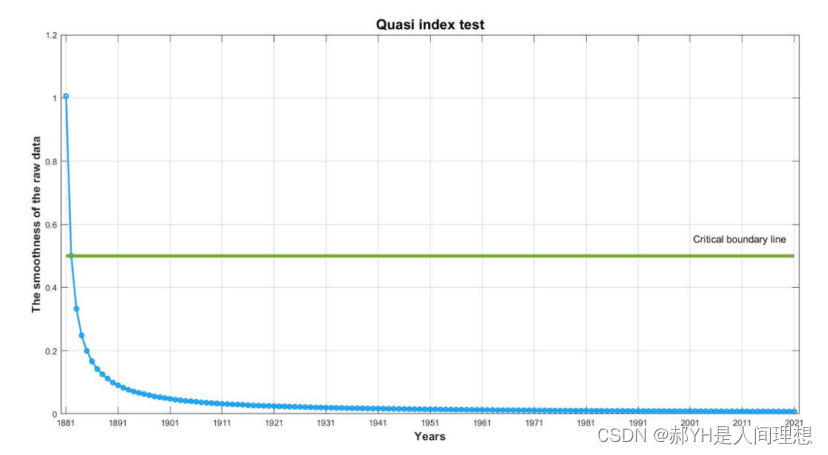
上图是准指数检验~
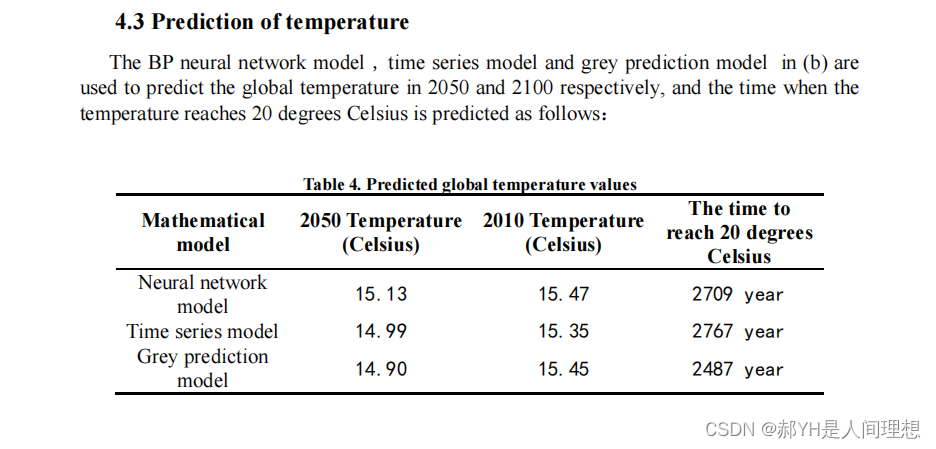 通过BP神经网络、多元线性回归以及灰色预测3种方式预测气温变化~结果可信度较高
通过BP神经网络、多元线性回归以及灰色预测3种方式预测气温变化~结果可信度较高
原文地址:https://blog.csdn.net/jsl123x/article/details/134543079
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_#ID#.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。