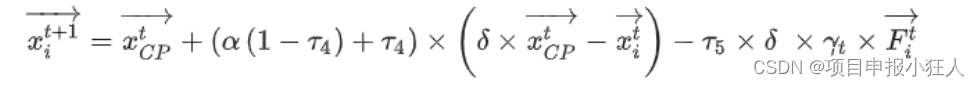贪心算法

贪心算法:基于某种情况进行一个排序。 贪心算法得到的是优良解,而非全局最优解。需要证明局部最优解 == 全局最优解
经典贪心算法 —— 会议问题

策略1:按照会议的持续时间长短来排序。持续时间短的会议优先安排
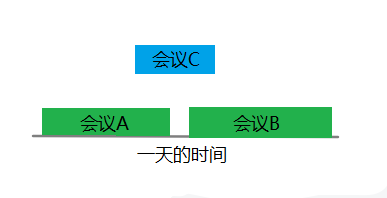
策略2:按照会议的开始时间早晚来排序。开始时间早的会议优先安排
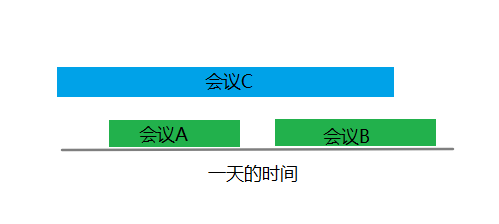
…….
策略n:按照会议的结束时间早晚来排序。结束时间早的会议优先安排
package greedyalgorithms;
import java.util.Arrays;
import java.util.Comparator;
public class ScheduleProgram {
class Progame {//会议
int start;
int end;
public Progame(int start, int end) {
this.start = start;
this.end = end;
}
}
public static class ProgameComparator implements Comparator<Progame> {
//按结束时间从早到晚排序
@Override
public int compare(Progame o1, Progame o2) {
return o1.end - o2.end;//o1的结束时间比o2的结束时间晚,o2排前面
//返回-1(或负数),表示不需要交换o1和o2的位置,o1排在o2前面
//返回1(或正数),表示需要交换o1和o2的位置,o2排在o1前面
}
}
//progames:需要安排的会议,timePoint:目前的时间点
public int bestArrange(Progame[] progames, int timePoint) {
Arrays.sort(progames, new ProgameComparator());//按照ProgameComparator比较器定义的compare()方法来排序
int result = 0;
for (int i = 0; i < progames.length; i++) {
if(timePoint <= progames[i].start){//此时时间 <= 会议的开始时间
result++;//安排好的会议的个数++
timePoint = progames[i].end;//时间来到会议的结束时间
}
}
return result;
}
}
对于这个策略,我们不能够轻松举出反例,但证明需要使用严格复杂的数学证明
贪心算法在笔试时的解题套路

1、准备暴力枚举、全排列的模板,贪心算法的最优解一定在全排列之中
2、贪心策略类题目,是一句某个标准排序或是放在堆里各自排序,举出n多个比较策略。此时容易举出反例的比较策略可以直接pass
3、用策略X结合随机大样本跑对数器。如果某个策略几千万次的随机样本都相同,那么这个比较策略就是正确的
贪心策略实现

切分金条的最小分割代价

从反方向考虑,已经切好的数组如何合并使得花费最小,花费的金额为合并的数值
如果有一组数组:arr = {2, 3, 4, 7, 9, 2}
| 将数组放入小根堆中 | arr = {2, 2, 3, 4, 7, 9} |
| 前两个数相加 | arr = {4, 3, 4, 7, 9} |
| 排序 | arr = {3, 4, 4, 7, 9} |
| 前两个数相加 | arr = {7, 4, 7, 9} |
| 排序 | arr = {4, 7, 7, 9} |
| 前两个数相加 | arr = {11, 7, 9} |
| 排序 | arr = {7, 9, 11} |
| 前两个数相加 | arr = {16, 11} |
| 排序 | arr = {16, 11} |
| 两个数相加 | arr = {27} |
package greedyalgorithms;
import java.util.PriorityQueue;
public class LessMoneySplitGold {
public static int lessMoney(int[] arr) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();//默认小根堆
for (int i = 0; i < arr.length; i++) {
priorityQueue.add(arr[i]);//将数组全部放入小根堆
}
int temp = 0;
while (priorityQueue.size() > 1) {
temp = priorityQueue.poll() + priorityQueue.poll();//弹出两个相加
priorityQueue.add(temp);//加回去,排序
}
return priorityQueue.poll();//最后小根堆中只有一个数即为结果
}
}做项目获得的最大收益

这里的花费仅仅表示做项目的门槛,因为在实际题目的计算中并没有减去项目花费的数
实现解析
一组项目:<花费,利润>
<2,3>, <1,4>, <1,1>, <2,7>., <3,2>, <4,10>
将项目放入一个以花费为依据的小根堆中,其中,利润的大小不考虑
小根堆中的项目表示都是锁住(不可做)的状态
小根堆中:<1,4>, <1,1>, <2,3>, <2,7>., <3,2>, <4,10>
依据初始资金m,解锁所有花费小于等于m的项目放到一个以利润为依据的大根堆中,其中,花费的大小不考虑
大根堆中的项目表示解锁(可做)的状态
m = 1; 大根堆中:<1,4>, <1,1>
大根堆抛出第一个项目,初始资金更新为m+该项目的利润
依据新的初始资金m,在小根堆中解锁项目,在大根堆中抛出,更新利润 …….
此外,还有另一种情况。当没有达到指定的项目数k,但某一时刻的初始资金比较少,不能够解锁小根堆中剩下的所有项目,此时只能提前返回当前的资金m
package greedyalgorithms;
import java.util.*;
public class FindMaxmizedCapital {
int M = 0;//初始资金
int K = 0;//表示最多做k个项目
class Program {
public int cost;//花费
public int profit;//利润
public Program(int cost, int profit) {
this.cost = cost;
this.profit = profit;
}
}
public int findMaxmizedCapital(List<Program> programs, int M, int K) {
PriorityQueue<Program> minCostPQ = new PriorityQueue(new MinCostComparator());
PriorityQueue<Program> maxProfitPQ = new PriorityQueue(new MaxProfitComparator());
//全部放入小根堆中锁定
for (Program pr : programs) {
minCostPQ.add(pr);
}
for (int i = 0; i < K; i++) {
//peek(): 获取元素但不删除队列首元素
while (!minCostPQ.isEmpty() && minCostPQ.peek().cost <= M) {
maxProfitPQ.add(minCostPQ.poll());//放入大根堆中,解锁
}
//更新初始资金
M += maxProfitPQ.poll().profit;
//当没有达到指定的项目数k,但某一时刻的初始资金比较少,不能够解锁小根堆中剩下的所有项目,此时只能提前返回当前的资金m
if (maxProfitPQ.isEmpty()) {
break;
}
}
return M;
}
class MinCostComparator implements Comparator<Program> {
@Override
public int compare(Program o1, Program o2) {
return o1.cost - o2.cost;
//compare()方法比较o1,o2的大小
//正序:当o1<o2时return -1,o1=o2时return 0,o1>o2时return 1
}
}
class MaxProfitComparator implements Comparator<Program> {
@Override
public int compare(Program o1, Program o2) {
return o2.profit - o1.profit;
}
}
}
原文地址:https://blog.csdn.net/m0_73530538/article/details/134582374
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_6357.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!