C++算法入门练习——最短路径-多路径

本文介绍: 而后我们要遍历这个 pre，当到达递归边界（v==s）时候，把路径加入到结果 paths中保存，然后 temp path 弹出，继续寻找其他的路径。），每条边有各自的边权，代表两个城市之间的距离。而遇见d[u]+G[u][j].wei g ht==d[newv]时，只需把这个新的路径结点也加入即可。而这个存储的是逆序，我们需要对每一条路径做一次逆序，然后再进行排序，从而进行输出。当我们遇见d[u]+G[u][j].weight<d[newv]时候，需要对之前的p re[newv]进行清空，重新存放。

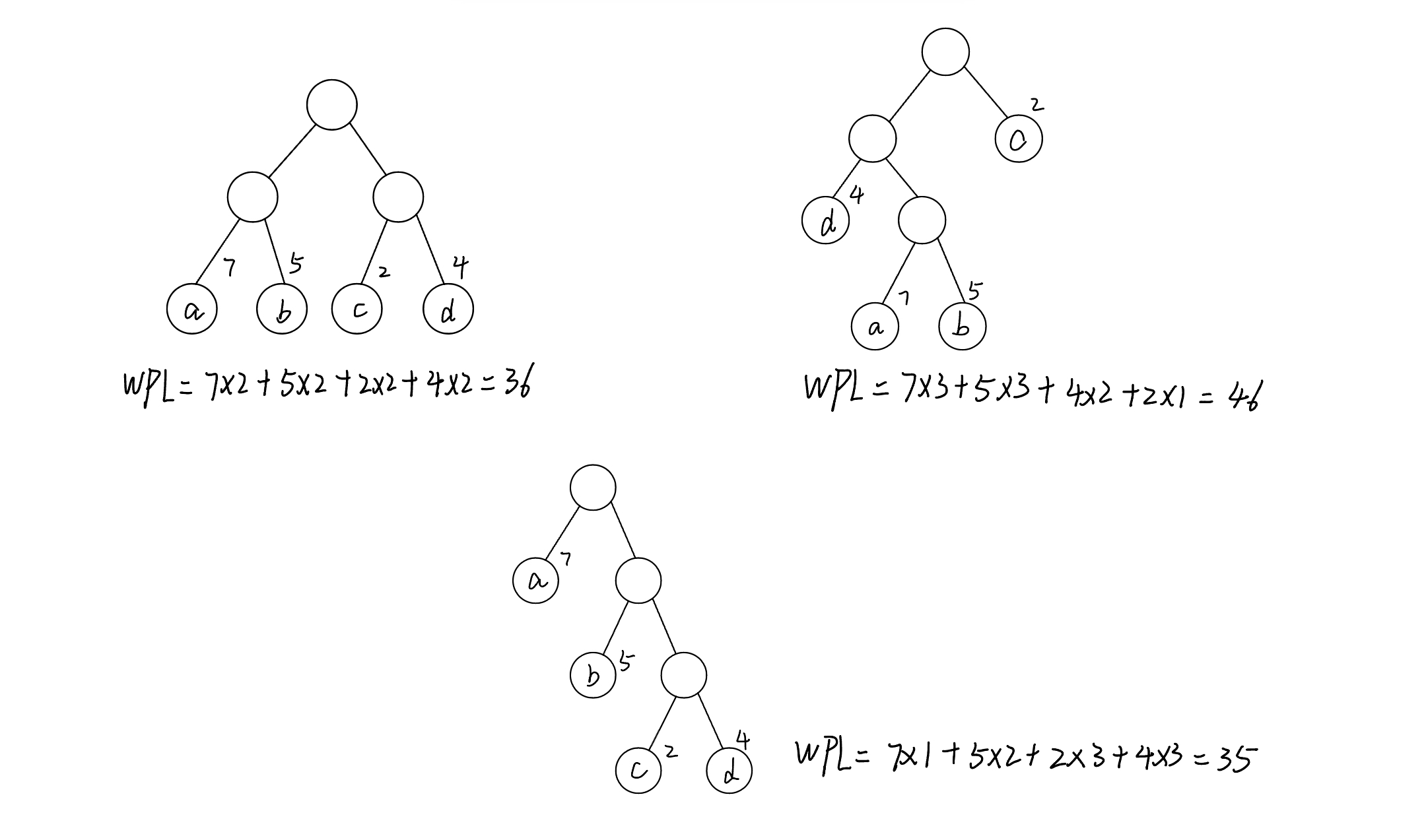
现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有各自的边权，代表两个城市之间的距离。求从s号城市出发到达t号城市的最短路径条数和最短路径（可能有多条）。

解题思路：

Di jk str a 算法的改进。

由于这里最短路径有可能有多个，因此单纯设置一个 p re 数组记录结点的父亲结点行不通。而也给出了解决方法，改用vector 可变数组。

当我们遇见d[u]+G[u][j].weigh t<d[newv]时候，

需要对之前的p re[newv]进行清空，重新存放。

而遇见d[u]+G[u][j].weigh t==d[newv]时，只需把这个新的路径结点也加入即可。

而后我们要遍历这个pre，当到达递归边界（v==s）时候，把路径加入到结果 paths中保存，然后temp path 弹出，继续寻找其他的路径。

而这个存储的是逆序，我们需要对每一条路径做一次逆序，然后再进行排序，从而进行输出。

完整代码如下：

#include &lt;iostream&gt;
#include &lt;vector&gt;
#include &lt;cstring>
#include <algorithm>
using namespace std;

const int INF = 1000000000;
const int maxn = 101;
int n,t;

struct node{
	int v;
	int weight;
}; 

vector<node> G[maxn]; 
bool isvisited[maxn] = {false};
int d[maxn];
vector<int> pre[maxn];

void Dijkstra(int v){
	fill(d,d+maxn,INF);
	d[v] = 0;
	for(int i=0;i<n;i++){
		int u = -1,min = INF;
		for(int j=0;j<n;j++){
			if(!isvisited[j]&amp;&amp;d[j]<min){
				u = j;
				min = d[j];
			}
		}
		if(u==-1){
			return ;
		}
		isvisited[u] = true;
		for(int j=0;j<G[u].size();j++){
			int newv = G[u][j].v;
			if(!isvisited[newv]){
				if(d[u]+G[u][j].weight<d[newv]){
					pre[newv].clear();
					d[newv] = d[u]+G[u][j].weight;
					pre[newv].push_back(u);
				}
				else if(d[u]+G[u][j].weight==d[newv]){
					pre[newv].push_back(u);
				}
			}
		}
	}
}

vector<vector<int>> paths;
vector<int> temppath;

void minpath(int s,int v){
	if(v==s){
		temppath.push_back(v);
		paths.push_back(temppath);
		temppath.pop_back();
		return;
	}
	temppath.push_back(v);
	for(int i=0;i<pre[v].size();i++){
		minpath(s,pre[v][i]);	
	}
	temppath.pop_back();
}

int main(){
	int m,s;
	cin>>n>>m>>s>>t;
	int a,b,w;
	for(int i=0;i<m;i++){
		cin>>a>>b>>w;
		node temp;
		temp.v = b;
		temp.weight = w;
		G[a].push_back(temp);
		temp.v = a;
		G[b].push_back(temp);
	}
	Dijkstra(s);
	minpath(s,t);
	cout<<paths.size()<<endl;
	for (int i = 0; i < paths.size(); i++) {
        reverse(paths[i].begin(), paths[i].end());
    }
    sort(paths.begin(), paths.end());
	for(int i=0;i<paths.size();i++){
		for(int j=0;j<paths[i].size();j++){
			if(j!=0){
				cout<<"->";
			}
			cout<<paths[i][j];
		}
		cout<<endl;
	}
	return 0;
}