【论文阅读】DBL: Efficient Reachability Queries on Dynamic Graphs

Lyu Q, Li Y, He B, et al. DBL: Efficient reachability queries on dynamic graphs[C]//Database Systems for Advanced Applications: 26th International Conference, DASFAA 2021, Taipei, Taiwan, April 11–14, 2021, Proceedings, Part II 26. Springer International Publishing, 2021: 761-777.

Abstract

可达性查询是图形上的一个基本问题，在学术界和工业界得到了广泛的研究。由于图在许多应用程序中都会发生频繁的更新，因此，在可达性查询中提供良好性能的同时，支持有效的图更新至关重要。现有的解决方案是用有向无环图（DAG）对原始图进行压缩，并提出了高效的查询处理和索引更新技术。然而，他们专注于优化强连接组件（SCCs）保持不变的场景，并忽略了在SCCs更新时DAG维护的过高成本。在本文中，我们提出了DBL的一个有效的无数据库索引，以支持仅插入更新的动态图的可达性查询。DBL建立在两个互补的索引之上：动态地标（DL）标签和双向叶（BL）标签。前者利用地标节点来快速确定可到达的对，而后者通过索引图中的叶节点来修剪不可到达的对。我们通过在真实世界的数据集上进行的大量实验，以对抗在动态可达性指数上的最先进的方法来评估DBL。结果表明，DBL在索引更新方面实现了一个数量级的加速，同时仍然产生了具有竞争力的查询效率。

1 Introduction

给定一个图G和一对顶点u和v，可达性查询（q（u，v））是一个基本图操作，答案是否存在路径从uvG这个操作是一个核心组件支持许多应用在实践中，如在社交网络，生物复合物，知识图和交通网络。在过去的十年中，[24,5,22,17,25,18,20,26,21,9]已经开发了大量的基于索引的方法，并在处理具有数百万个顶点和边的静态图上的可达性查询方面取得了巨大的成功。然而，在许多情况下，图表是高度动态的[23]：新的友谊在脸书和推特等社交网络上不断形成；知识图随着新的实体和关系不断更新；交通网络在道路上发生变化正在进行施工和临时交通管制。在这些应用程序中，必须支持有效的图形更新，同时提供良好的可达性查询性能。
人们已经在努力开发可达性索引来支持图形更新[4,6,8,10,15,16,17]。然而，在这些工作中有一个主要的假设：图中底层图中的强连接组件（SCCs）在图更新后保持不变。有向无环图（DAG）将scc折叠成顶点，然后在一个比原始图小得多的图上处理可达性查询。因此，最先进的解决方案[27,24]依赖于DAG来设计一个高效查询处理的索引，但它们的索引维护机制只支持不在DAG中触发SCC合并/拆分的更新。然而，这种假设在实践中可能是无效的，因为边缘插入可能会导致DAG中的scc的更新。换句话说，在以前的研究中，DAG维护的开销大多被忽视了。
一个潜在的解决方案是采用现有的DAG维护算法，如[26]。不幸的是，这种DAG维护是一个非常耗时的过程，在实验中也证明了这一点。例如，在我们的实验中，更新 LiveJournal数据集中的一条边插入的DAG所花费的时间是处理最先进方法的100万个查询所花费的时间的两倍。因此，我们需要一种新的索引方案，维护成本低，同时有效地回答可达性查询。
在本文中，我们提出了一个无dag的动态可达性索引框架（DBL），它能够实现高效的索引更新，并支持在大规模图上同时进行快速查询处理。我们关注于不断添加新边和顶点的仅插入动态图。这是因为删除的数量通常明显小于插入的数量，并且在许多图形应用程序[2,3]中，删除是使用延迟更新来处理的。我们没有维护DAG，而是对两组顶点周围的可达性信息进行索引：具有高中心性的“地标”节点和具有低中心性的“叶”节点（例如，具有零内度或出度的节点）。由于地标节点和叶节点的可达性信息在图更新中保持相对稳定，与使用DAG的方法相比，它提供了高效的索引更新机会。因此，DBL建立在两个简单而有效的索引组件之上：(1)动态地标（DL）标签和(2)双向叶（BL）标签。在DBL中结合DL和BL，可以保证有效的索引维护，同时实现具有竞争力的查询处理性能。
高效的查询处理： DL的灵感来自于地标索引方法[5]。建议的DL标签维护一小部分地标节点作为图中每个顶点的标签。给定一个查询q（u，v），如果u和v的DL标签都包含一个共同的地标节点，我们可以立即确定u到达v。否则，我们需要调用广度优先搜索（BFS）来处理q（u，v）。我们设计了BL标签来快速修剪无法达到的顶点对，以限制昂贵的BFS的数量。BL是对DL的补充，它专注于在图中的叶节点周围构建标签。叶节点形成了一个排他性的集除了地标节点集之外。一个顶点u的BL标签被定义为可以到达u或u可以到达它们的叶节点。因此，如果u的BL标签中存在一个叶节点，而它不出现在v的BL标签中，则u不能到达v。总之，DL可以快速确定可达对，而补充DL的BL可以修剪断开的对来纠正那些DL不能立即确定的对。
有效的索引维护：DL和BL标签都是轻量级索引，其中每个顶点只存储一个恒定大小的标签。当插入新的边时，使用有效修剪的BFS，并且只访问其标签需要更新的顶点。特别是，一旦顶点的标签不受边缘更新的影响，我们就可以安全地从BFS中修剪顶点以及它的后代，从而实现有效的索引更新。
为了更好地利用现代体系结构的计算能力，我们采用简单而紧凑的位操作来实现DL和BL。我们的实现是基于OpenMP和CUDA，以便分别利用并行架构、多核cpu和图形pu（图形处理单元）。
在此，我们将这些贡献总结如下：
我们引入了DBL框架，它结合了两个互补的DL和BL标签，以实现在大型图上高效的可达性查询处理。
我们提出了一种新的针对DL和BL的索引更新算法。据我们所知，这是不保持DAG的动态可达性指数的第一个解决方案。此外，该算法还可以很容易地通过并行接口来实现。
我们进行了大量的实验来验证DBL的性能与最先进的动态方法[27,24]的比较。DBL实现了具有竞争力的查询性能和索引更新的数量级加速。我们还在多核和gpu的系统上实现了DBL，与我们的顺序实现相比，我们展示了显著的性能提高。
本文的其余部分组织如下。第二节介绍了初步工作和背景工作。第3节介绍了相关的工作。第4节介绍了索引定义和查询处理。第5节展示了DL和BL标签的更新机制。第6节报告了实验结果。最后，我们在第7节中总结了论文。

2 Preliminaries

一个有向图被定义为G =（V，E），其中V是顶点集，E是带有n个= |V |和m个= |E|的边集。我们将从顶点u到顶点v的一条边表示为（u，v）。G中从u到v的路径表示为P ath（u，v）= (u，w1，w2，w3，…其中∈和相邻的顶点连接的边缘G我们说v是由u当存在一个P∈（u，v）在G，此外，我们使用子（∈）表示u的直接继承人和u的直接前辈表示为P re (u)。同样地，我们把u（包括u）所有的祖先表示为Anc (u)，并且u（包括u）的所有后代为Des (u)。我们将G的反过来的图表示为G‘=（V，E’），其中G的所有边都在G‘的相反方向上。在本文中，正向是指在G‘的边缘上遍历。对称地，反向是指在G’的边缘上遍历。我们将q（u，v）表示为从u到v的可达性查询。本文研究了图中的动态情况。表1总结了常见的符号。

3 Related Work

对动态图[4,6,8,10,15,16,17]有一些研究。Yildirim等人提出匕首[26]，在插入和删除后将图保持为DAG。该索引构建在DAG上，以方便可达性查询处理。DAG维护的主要操作是强连接组件（SCC）的合并和拆分。不幸的是，匕首在处理大型图形时（即使顶点只有数百万个[27]）的查询处理性能也不理想。
最先进的方法： TOL [27]和IP [24]采用匕首式对DAG的维护方法，在DAG上提出新的动态指标，以提高查询处理性能。我们注意到，TOL和IP只适用于DAG中的SCC/s对更新保持不变的情况。在SCC合并/崩溃的情况下，仍然需要匕首来恢复SCC/s。例如，TOL和IP可以处理图1(a)中的边缘插入（v1、v5），而不需要调用匕首。但是，当插入（v9、v2）时，两个SCC/s {v2}和{v5、v6、v9}将合并为一个较大的SCC {v2、v5、v6、v9}。对于这种情况，TOL和IP首先依赖于匕首来维护DAG，然后执行它们各自的方法来进行索引维护和查询处理。
然而，SCC维护的费用被排除在他们的实验[27,24]中，这样的费用实际上是不可忽视的[26,14]。
在本文中，我们提出了一个DBL框架，它只维护图中所有顶点的标签，而不构造DAG。这意味着，DBL可以有效地避免在图形更新时进行昂贵的DAG维护。DBL通过最先进的解决方案（即TOL和IP）实现了具有竞争力的查询处理性能，同时在索引更新方面提供了数量级的加速。

4 DBL Framework

DBL框架由DL和BL标签组成，它们具有独立的查询和更新组件。在本节中，我们将介绍DL和BL标签。然后，我们设计了一种基于DBL索引的查询处理算法。

4.1 Definitions and Construction

我们提出了由两个索引组件组成的DBL框架： DL和BL。
定义1 (DL标签）。给定一个地标顶点集L⊂V和|L| = k，我们为每个顶点v∈V定义两个标签： DLin (v)和DLout (v)。DLin (v)是L中可以到达v的节点的子集，而DLout (v)是L中v可以到达的节点的子集。
需要注意的是，DL标签是2跳标签[5]的一个子集。事实上，当地标设置为L = V时，DL标签的特殊情况是DL标签。然而，我们发现在动态图场景中保持2-Hop标签会导致索引爆炸。因此，我们建议只选择一个顶点的子集作为地标集L来索引DL标签。这样，DL标签具有高达O（n|L|）的空间复杂度，通过调整L的选择可以很容易地控制索引大小。下面的引理显示了DL标签在可达性查询处理中的一个重要特性。
引理1。给定两个顶点u，v及其对应的DL标签，DLout (u)∩DLin (v) =∅推导出u到达v，但反之亦然。
例子1。我们在图1(a).中展示了一个正在运行的示例假设选择地标集为{v5，v8}，对应的DL标签如图1(b).所示q（v1，v10）返回true，因为DLout（v1）∩DLin（v10）= {v8}。然而，尽管有DLout（v3）∩DLin（v11）=∅，但标签还是不能对q（v3，v11）给出否定的答案。这是因为从v3到v11的路径上的中间顶点v7不包括在地标集中。

为了实现良好的查询处理性能，我们需要选择一组顶点作为地标，这样它们可以覆盖图中大部分可达顶点对，即DLout(u)∩DLin(v)包含至少一个任意可达顶点对u和v。最优的地标选择已被证明是np硬[13]。本文采用一种启发式的方法来选择DL标签节点。特别地，我们用M (u) = |P re (u)|·|Suc (u)|对顶点进行排序，以近似它们的中心性，并选择前k个顶点。其他的地标选择方法也将在第6.2节中进行讨论。
定义2 (BL标签）。BL为每个顶点v∈V引入了两个标签： BLin (v)和BLout (v)。BLin (v)包含所有可以达到v的零度内顶点，而BLout (v)包含v可以达到的所有零度外顶点。为了方便起见，我们将内度或出度为零的顶点称为叶节点。
引理2。给定两个顶点u，v及其对应的BL标签，如果BLout(v)6⊆BLout (u)或BLin(u)6⊆BLin (v)，u不能达到G中的v。
BL标签可以给出q (u、v）的否定答案。这是因为如果你可以达到v，那么你就可以到达v可以到达的所有叶节点，而所有到达u的叶节点也应该达到v。DL标签对于给予可达性查询的积极答案是有效的，而BL标签通过剪枝不可达的对来发挥互补的作用。在本文中，我们以内度/出度为零的顶点作为叶节点。我们还将在第6.2节中讨论其他的叶片选择方法。
例子2。图1©显示了正在运行的示例的BL标签。BL标签对BLin（v6）的回答是否定的，因为BLin（v4）不包含在q（v6）中。直观地说，顶点v1到达顶点v4，但不能到达v6，这说明v4不应该到达v6。BL标签不能给出肯定的答案。以q（v5、v2）为例，标签满足包含条件，但不能给出肯定的答案。
BL标签节点的数量可能会很大。为了开发高效的索引操作，我们为BL构建了一个大小为k‘的哈希集，如下所示。BLin和BLout都是{1,2，……，k‘}的子集，其中k’是用户定义的标签大小，它们存储在位向量中。一个哈希函数用于将叶节点映射到相应的位。对于我们的例子，叶子是{v1、v2、v3、v10、v11}。当k‘=2时，所有的叶子都被散列为两个唯一的值。假设h（v1）= h（v10）= 0，h（v2）= h（v3）= h（v11）= 1。我们在图1©中显示了其中所表示的散列BL标签集如h（BLin）和h（BLout）。在本文的其余部分中，我们直接使用BLin和BLout来表示相应标签的哈希集。值得注意的是，我们仍然可以使用引理2来修剪与散列BL标签不可到达的对。

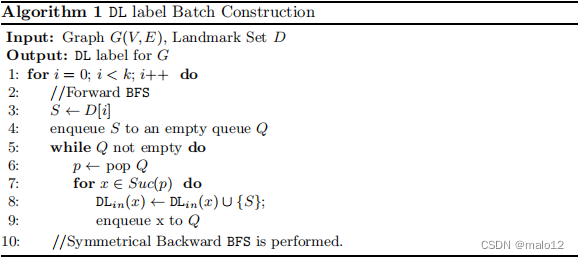
我们简要讨论了DBL的批索引构建，因为本工作的重点是动态场景。算法1提出了DL标签的构造，该算法遵循现有的2跳标签[5]的工作。对于每个地标节点D[i]，我们从S（Line 4）开始一个BFS，并在S可以到达的每个顶点（行5-9）的DLin标签中包含S。为了构造DLout，我们在反向图G‘对称执行BFS（第10行）执行BFS。为了构造BL标签，我们只需简单地将地标集D替换为叶集D‘，并将S替换为算法1中散列到桶i（Line 3）的所有叶节点。构建DBL的复杂性是O（（k+k‘）（m+n））。
请注意，尽管我们使用[5]来构建离线索引，但我们工作的贡献是，我们将DL和BL作为高效查询处理的补充索引。此外，我们是第一个在不假设SCC/s保持不变的情况下支持高效的动态可达性指数维护的工作。空间复杂性。DL和BL标签的空间复杂度分别为O（kn）和O（k‘n）。

4.2 Query Processing

算法2利用这两个索引，给出了DBL的查询处理框架。给定一个可达性查询q（u，v），如果标签足以确定可达性（第6-9行），我们将立即返回答案。根据DL和BL标签的定义，如果它们的DL标签重叠，u达到v（第6行），如果它们的BL标签不重叠，u没有达到v（第9行）。此外，在第10行和第12行中分别执行了两个早期终止规则。第10行使用了SCC中的所有顶点都包含至少一个公共地标节点的属性。第12行利用了当u或v与一个地标节点l共享相同的SCC时，那么当且仅当l出现在u和v的DL标签中时，u才到达v。我们用定理1和定理2证明了它们的正确性。否则，我们将转向具有有效修剪的BFS搜索。BFS中的修剪如下执行如下。在访问一个顶点q时，该程序将确定该顶点q是否应该在第20行和第22行中排队。BL和DL标签将判断目标顶点v是否在Des (w)中。如果没有，q将从BFS中删除，以在使用BFS遍历图之前快速回答查询。

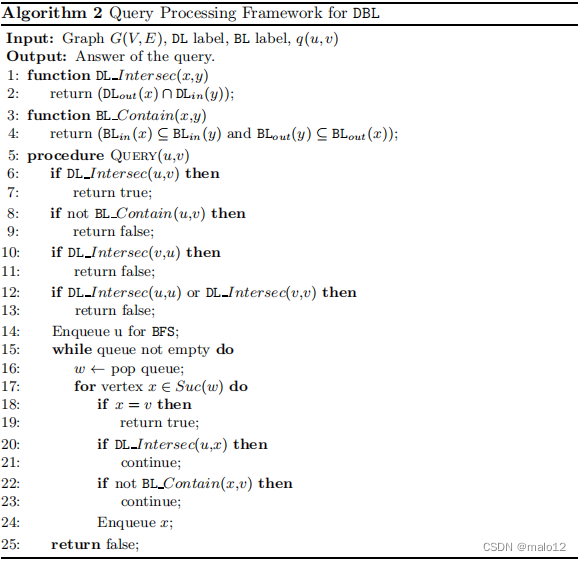
定理1。在算法2中，当DL Intersec（x，y）返回false，而DL Intersec（y，x）返回true时，则x不能达到y。
证明。DL Intersec（y，x）返回true表示顶点y到达x。如果顶点x到达顶点y，则y和x必须在同一个SCC中（根据SCC的定义）。由于SCC中的所有顶点都是相互可达的，因此DLout (y)∩DLin (x)中的地标节点也应该包含在同一SCC中的所有顶点的DLout和DLin标签中。这意味着DL Intersec（x，y）应该返回true。因此x不能到达y，否则它与DL Intersec（x，y）返回false的事实相矛盾。
定理2。在算法2中，如果DL Intersec（x，y）返回false，DL Intersec（x，x）或DL Intersec（y，y）返回true，那么顶点x不能达到y。
证明。如果DL Intersec（x，x）返回true，这意味着顶点x是地标或x与地标在同一SCC中。如果x与地标l在同一个SCC中，则顶点x和顶点l应该具有相同的可达性信息。作为地标，l将把其标签元素l推到Anc (l)中所有顶点的DLout标签，以及Des (l)中所有顶点的DLin标签。地标l的可达性信息将被完全覆盖。这意味着x的可达性信息也被完全覆盖了。因此，DL标签足以回答不需要BFS的查询。因此，如果DLInttersec（x，y）返回false，则x无法访问y。当DL Intersec（y，y）返回true时，证明过程也类似。
查询复杂性。给定一个查询q（u，v），当该查询可以通过DL和BL标签直接回答时，时间复杂度为O（k+k‘）。否则，我们转向修剪过的BFS搜索，它的最坏情况下的时间复杂度为O（k+k‘）（m+n）)。设ρ表示其可达性可由标签直接回答的顶点对的比率。摊余时间复杂度为O（ρ（k+k‘）+（1−ρ）（k+k’）（m+n））。根据经验，根据我们的实验（第6节中的表4），ρ的比例超过了95%，这意味着高效的查询处理。

5 DL and BL Update for Edge Insertions

当插入一条新边（u、v）时，角度(u)中的所有顶点都可以到达Des (v)中的所有顶点。在较高的层次上，所有可以到达u的地标节点也应该到达Des (v)中的顶点。换句话说，v可以到达的所有地标节点也应该由Anc (u)中的顶点到达。因此，我们通过1)更新标签，将所有∈∈(v)添加DLin (u)到DLin (x)中；2)将所有∈Anc (u)的DLout (v)添加到DLout (x)中。

算法3描述了DLin的边缘插入场景。我们省略了对DLout的更新，它是与DLin对称的。如果DL标签可以在边插入之前确定原始图中的顶点u可以到达顶点v，则插入将不会触发任何标签更新（第1行）。第2-8行描述了一个BFS过程与修剪。对于一个访问的顶点x，我们不遍历Des(x)ifin(u)⊆DLin (x)，因为Des (x)中的所有顶点都被认为不受影响，因为它们的DLin标签是DLin (x)的超集。
例子3。图2(a)显示了一个边缘插入的示例。图2(b)显示了相应的DLin标签更新过程。DLin标签用括号表示。如果插入一条边（v9、v2）， 则将DLin（v9）复制到DLin（v2）。然后将对DLin（v5）和DLin（v6）进行检查。由于DLin（v9）是DLin（v5）和DLin（v6）的子集，因此顶点v5和顶点v6从BFS中删除。然后，将终止更新进程。

DL标签只对可达性查询提供了积极的答案。在连接性较差的图中，DL将退化为昂贵的BFS搜索。因此，我们使用双向叶（BL）标签来补充DL，并快速识别不可到达的顶点对。我们省略了BL的更新算法，因为它们与DL的非常相似，除了更新应用于BLin和BLout标签。图2©显示了BLin标签的更新情况。与DL标签类似，更新过程将提前终止，因为BLin（v2）在边缘插入后完全不受影响。因此，在这种情况下，将不会更新BLin标签。
更新DBL的复杂性。在最坏的情况下，将访问已到达或可到达更新边的所有顶点。因此，DL和BL的时间复杂度为O（k+k‘）（m+n）)，其中（m + n）是BFS的成本。根据经验，由于BFS过程将修剪大量的顶点，因此实际的更新过程比普通的BFS要有效得多。

6 Experimental Evaluation

在本节中，我们通过比较所提出的DBL框架与在动态图的可达性查询方面的最先进的方法来进行实验。

6.1 Experimental Setup

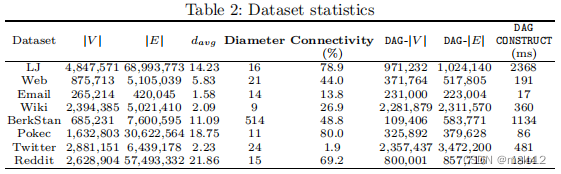
环境：我们的实验是在一个拥有IntelXeonCPUE5-2640v4 2.4 GHz，256GBRAM和特斯拉P100 PCIe版本的GPU的服务器上进行的。数据集：我们在8个真实世界的数据集上进行了实验（见表2）。我们从SNAP [11]中收集了以下数据集。LJ和Pokec是两个社交网络，它们在本质上是幂律图。BerkStan和Web是网络图，其中节点表示网页，有向边表示它们之间的超链接。维基百科和电子邮件都是通信网络。Reddit和推特是来自[23]的两个社交网络数据集。

6.2 Label Node Selection

DL通过启发式地将一个顶点u的中心性近似为M (u) = |P re (u)|·|Suc (u)|来选择地标节点。在这里，我们评估了不同的启发式方法的地标节点选择。结果如表3所示。

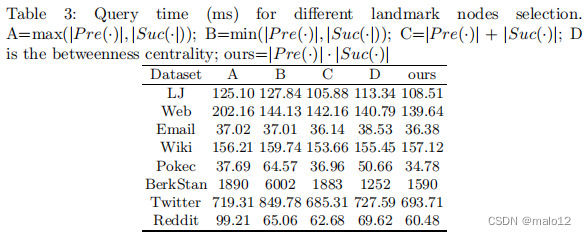
总的来说，我们采用的启发式算法（|P re (u)|·|Suc (u)|）达到了性能。对于电子邮件和Wiki，所有的方法都具有相似的性能。|Pre（·）|+|Suc（·）|和|Pre（·）|·|Suc（·）|在其他数据集中获得了更好的性能。最后，|Pre（·）|+|Suc（·）|（度中心性）和|Pre（·）|·|Suc（·）|对大多数数据集提供类似的性能，后者在伯克斯坦数据集更优越。因此，我们采用|Pre（·）|·|Suc（·）|来近似于中心性。需要指出的是，尽管中间性中心性获得了中等的整体性能，但它在BerkStan数据集中显示了最好的性能。
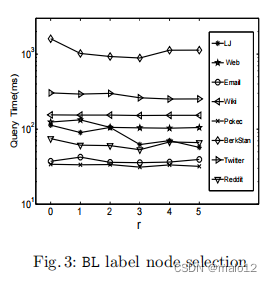
在本文的主体中，我们将叶节点限制为度零或度零的叶节点。然而，我们提出的方法不需要这样的限制，并且有可能选择任何顶点作为叶节点。根据我们选择DL标签节点的方法，我们使用M (u) = |P re (u)|·|Suc (u)|来近似顶点u的中心性，如果M (u)≤r，其中r是一个调优参数，则选择顶点u作为BL标签节点。分配r = 0产生了本文正文中提出的特殊情况。对新的BL标签进行查询处理和索引更新的算法保持不变。图3显示了当我们改变阈值r时，DBL的查询性能。r越高，就会选择更多的顶点作为叶节点，这在理论上可以提高查询处理效率。然而，由于我们对BL标签使用了哈希函数，更多的叶节点会导致更高的碰撞率。这就解释了为什么我们没有观察到在查询性能方面的显著改进。

6.3 Effectiveness of DL+BL

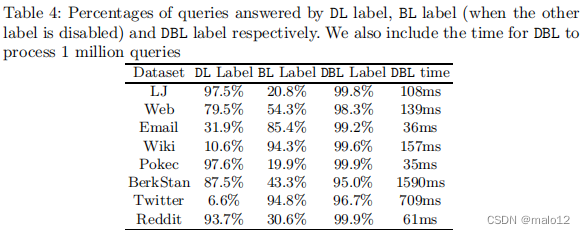
表4显示了由DL标签、BL标签（当其他标签被禁用时）和DBL标签回答的查询的百分比。所有的查询都是随机生成的。结果表明，DL对密集和高度连通的图（LJ、Pokec和Reddit）有效，而BL对稀疏和连接较差的图（电子邮件、Wiki和Wiitter）有效。然而，如果该标签被禁用，我们仍然会招致昂贵的BFS。通过结合这两个指标的优点，我们的建议导致了显著更好的性能。DBL可以比DL和BL标签回答更多的查询。研究结果证实了我们提出的DL和BL是互补的主张。我们注意到，对DBL的查询处理是能够进行的为大多数数据集处理具有亚秒延迟的100万个查询，这显示了出色的性能。

标签大小：对DBL查询处理的影响。在DBL中有两个标签：DL和BL都在位向量中存储标签。DL标签的大小取决于所选的地标节点的数量，而BL标签的大小取决于选择了多少哈希值来索引叶节点。我们评估了所有的数据集，以显示表5中每个顶点不同的DL和BL标签大小的性能趋势（通过处理100万个查询）。

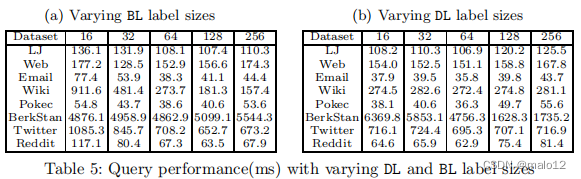
当改变DL标签大小k时，大多数数据集的性能在一定大小（如64）之前保持稳定，之后恶化。这意味着额外的地标节点将覆盖很少的额外的可达性信息。因此，选择更多的地标节点并不一定会导致更好的整体性能，因为处理额外位的成本会导致额外的缓存丢失。BerkStan从增加DL标签大小到128中获益，因为64个地标不足以覆盖足够的可达对。
与DL标签相比，一些数据集在改变BL标签的大小时得到了一个最佳点。这是因为有两个相互冲突的因素会影响整体表现。随着BL标签大小的增加和更多的哈希值的合并，我们可以通过检查BL标签来快速修剪更多不可到达的顶点对，而不使用BFS遍历图。此外，更大的BL大小也可以提供更好的BFS剪枝能力，即使它不能直接回答查询（算法2）。然而，标签处理的成本随着BL标签尺寸的增加而增加。根据我们的参数研究，我们将Wiki的DL和BL标签大小设置为64和256，BerkStan的DL和BL标签大小设置为128和64。对于其余的数据集，DL和BL标签大小均设置为64。

6.4 General Graph Updates

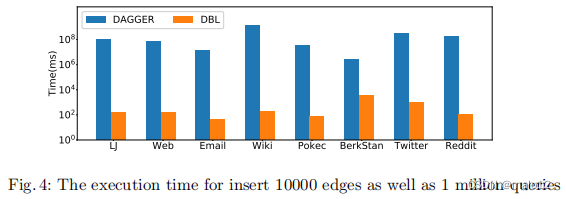
在本节中，我们将评估DBL在一般图更新上的性能。由于匕首是唯一可以处理一般更新的方法，我们在图4中将DBL与匕首进行比较。分别随机生成和执行1万条边缘插入和100万个查询。不同于匕首，DBL不需要维护DAG，因此，在所有的数据集中，DBL可以实现巨大的性能提升。对于边缘插入和查询，DBL都比匕首快几个数量级。最小的性能差距在于伯克斯坦。这是因为伯克斯坦的直径很大。因为DBL依赖于BFS遍历来更新索引。遍历开销对它的性能至关重要。BerkStan的直径很大，这意味着，在索引更新期间，DBL需要遍历额外的跳数来更新索引，这将大大降低性能。

6.5 Synthetic graph updates

在本节中，我们将我们的方法与IP和TOL进行比较。与可以处理真实世界更新的DBL不同，IP和TOL只能处理合成的不会触发DAG维护的边缘更新。因此，对于IP和TOL，我们遵循他们在论文[27,24]中描述的实验设置。具体来说，我们从DAG中随机选择10,000条边并删除它们。然后，我们将返回插入相同的边。这样，我们就可以在不触发DAG维护的情况下获得边缘插入性能。对于DBL，我们坚持使用一般的图形更新。边缘插入将被随机生成并执行。之后将执行100万个查询。需要注意的是，尽管IP和TOL都声称它们可以处理动态图，但由于它们特殊的前提条件，它们的方法实际上在现实场景中的使用有限。

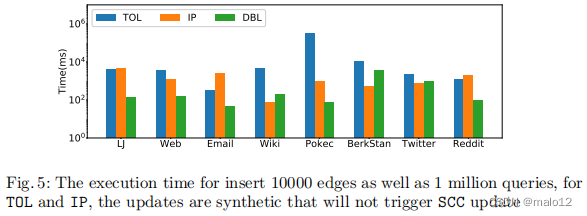
结果如图5所示。除了在三个数据集（Wiki、BerkStan和Twitter）外，DBL在大多数情况下都优于其他基线，在这三个数据集上，IP可以实现更好的性能。然而，在几何平均性能方面，DBL的性能分别比IP和TOL高出4.4倍和21.2倍。我们分析了Wiki、BerkStan和Twitter上DBL比IP慢的原因。正如我们所述，DBL依赖于修剪的BFS来更新索引，BFS遍历速度将决定最坏情况的更新性能。伯克斯坦的最大直径为514，Wwitter的第二大直径为24，这极大地降低了DBL的更新程序。对于Wiki，DBL仍然可以获得比IP更好的更新性能。然而，IP在查询处理方面效率更高，从而导致更好的整体性能。
虽然这个实验场景已经在以前的研究中使用过，但对DBL的比较是不公平的。由于IP和TOL都依赖于DAG来处理查询和更新，它们的合成更新从实验中排除了DAG维护过程/开销。然而，DAG维护对于他们处理真实世界的边缘更新的方法是至关重要的，正如我们如图4所示，开销是不可忽略的。

6.6 Parallel Performance

我们使用OpenMP和CUDA（分别为DBL-P和DBL-G）实现了DBL，以演示在多核cpu和gpu上的部署，实现了令人鼓舞的查询处理加速。我们遵循现有的基于gpu的图形处理管道，对查询进行批处理并更新[7,19,12]。请注意，传输时间可以与GPU处理重叠，以最小化数据通信成本。CPU和GPU的实现都是基于以顶点为中心的框架。

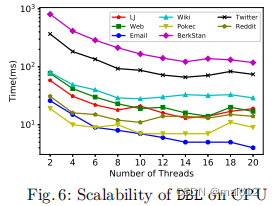
为了验证并行方法的可伸缩性，我们改变了在DBL-P中使用的线程的数量，并在图6中显示了其性能趋势。DBL-P在线程数量的增加下实现了几乎线性的可伸缩性（注意，圆轴是以对数尺度绘制的）。当线程数超过14个时，可伸缩性的线性趋势趋于消失。我们把这一观察结果归因为处理任务的内存带宽约束性质。一旦标签无法回答查询，并且BFS的效率在很大程度上受到CPU内存带宽的限制，DBL就会调用BFS遍历。这个cpu的内存带宽限制问题可以通过使用提供内存带宽提升的gpu来解决。
所比较的查询处理性能如表6所示。双向BFS（B-BFS）查询被列为一个基线。我们还将我们的并行解决方案与自制的IP的OpenMP实现（表示为IP-P）进行了比较。在OpenMp实现中使用了20个线程。我们注意到，如果IP的标签不能确定查询结果，则它必须调用已修剪过的DFS。DFS在本质上是一个顺序的过程，不能有效地并行化。对于我们的并行实现IP-P，我们分配了一个线程来处理一个查询。我们有以下的观察结果。

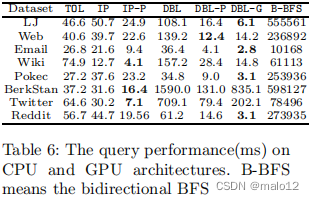
首先，DBL建立在修剪后的BFS上，它可以与顶点中心范式有效地并行化。我们已经观察到，通过并行执行可以显著地提高性能。DBL-P（cpu）可以在所有数据集上得到4倍到10倍的加速。DBL-G（gpu）显示出更好的性能。相比之下，由于DFS在IP-P中频繁发生随机访问，性能受到内存带宽的限制。因此，与顺序并行化相比，并行化并没有给IP-P带来太多的性能增益。
其次，DBL提供了与IP-P竞争的效率，但在比较单线程性能时，DBL可能比TOL和IP慢。然而，这是通过假设DAG结构来实现的，但是基于DAG的方法会产生非常高的索引更新成本，正如我们在前面的小节中所演示的那样。相比之下，DBL在处理100万个查询时实现了亚秒的查询处理性能，同时仍然不使用DAG而支持有效的更新。
第三，有些情况下DBL-P优于DBL-G，即Web、伯克斯坦和Twitter。这是因为这些数据集的直径比其他数据集的直径要高，而修剪后的BFS需要遍历额外的跳数来确定可达性。因此，我们产生了更多的随机访问，这并不适合GPU架构。

7 Conclusion

在这项工作中，我们提出了DBL，一个索引框架，以支持在增量图上的动态可达性查询处理。据我们所知，DBL是避免维护DAG结构来构建和构建可达性指数的第一个解决方案。DBL利用了两个互补的索引组件： DL和BL标签。DL标签建立在地标节点上，以确定由地标连接的可达顶点对，而BL标签通过检查其在图中叶节点上的可达性信息来修剪不可达顶点对。实验评估表明，连续的DBL版本在索引更新方面优于最先进的解决方案，具有数量级的加速，同时表现出具有竞争力的查询处理性能。在多核和gpu上的DBL并行实现进一步提高了我们的顺序实现的性能。作为未来的工作，我们感兴趣的是扩展DBL以支持删除，这将在许多应用程序中得到延迟的支持。

代码007普通

打赏 收藏 海报 链接