Abstract
可达性查询是图形上的一个基本问题,在学术界和工业界得到了广泛的研究。由于图在许多应用程序中都会发生频繁的更新,因此,在可达性查询中提供良好性能的同时,支持有效的图更新至关重要。现有的解决方案是用有向无环图(DAG)对原始图进行压缩,并提出了高效的查询处理和索引更新技术。然而,他们专注于优化强连接组件(SCCs)保持不变的场景,并忽略了在SCCs更新时DAG维护的过高成本。在本文中,我们提出了DBL的一个有效的无数据库索引,以支持仅插入更新的动态图的可达性查询。DBL建立在两个互补的索引之上:动态地标(DL)标签和双向叶(BL)标签。前者利用地标节点来快速确定可到达的对,而后者通过索引图中的叶节点来修剪不可到达的对。我们通过在真实世界的数据集上进行的大量实验,以对抗在动态可达性指数上的最先进的方法来评估DBL。结果表明,DBL在索引更新方面实现了一个数量级的加速,同时仍然产生了具有竞争力的查询效率。
1 Introduction
给定一个图G和一对顶点u和v,可达性查询(q(u,v))是一个基本图操作,答案是否存在路径从uvG这个操作是一个核心组件支持许多应用在实践中,如在社交网络,生物复合物,知识图和交通网络。在过去的十年中,[24,5,22,17,25,18,20,26,21,9]已经开发了大量的基于索引的方法,并在处理具有数百万个顶点和边的静态图上的可达性查询方面取得了巨大的成功。然而,在许多情况下,图表是高度动态的[23]:新的友谊在脸书和推特等社交网络上不断形成;知识图随着新的实体和关系不断更新;交通网络在道路上发生变化正在进行施工和临时交通管制。在这些应用程序中,必须支持有效的图形更新,同时提供良好的可达性查询性能。
人们已经在努力开发可达性索引来支持图形更新[4,6,8,10,15,16,17]。然而,在这些工作中有一个主要的假设:图中底层图中的强连接组件(SCCs)在图更新后保持不变。有向无环图(DAG)将scc折叠成顶点,然后在一个比原始图小得多的图上处理可达性查询。因此,最先进的解决方案[27,24]依赖于DAG来设计一个高效查询处理的索引,但它们的索引维护机制只支持不在DAG中触发SCC合并/拆分的更新。然而,这种假设在实践中可能是无效的,因为边缘插入可能会导致DAG中的scc的更新。换句话说,在以前的研究中,DAG维护的开销大多被忽视了。
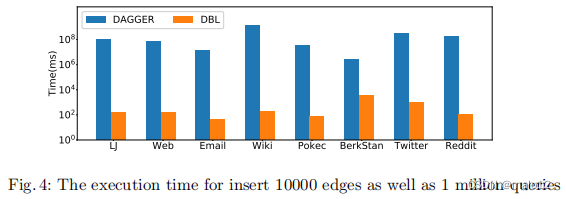
一个潜在的解决方案是采用现有的DAG维护算法,如[26]。不幸的是,这种DAG维护是一个非常耗时的过程,在实验中也证明了这一点。例如,在我们的实验中,更新 LiveJournal数据集中的一条边插入的DAG所花费的时间是处理最先进方法的100万个查询所花费的时间的两倍。因此,我们需要一种新的索引方案,维护成本低,同时有效地回答可达性查询。
在本文中,我们提出了一个无dag的动态可达性索引框架(DBL),它能够实现高效的索引更新,并支持在大规模图上同时进行快速查询处理。我们关注于不断添加新边和顶点的仅插入动态图。这是因为删除的数量通常明显小于插入的数量,并且在许多图形应用程序[2,3]中,删除是使用延迟更新来处理的。我们没有维护DAG,而是对两组顶点周围的可达性信息进行索引:具有高中心性的“地标”节点和具有低中心性的“叶”节点(例如,具有零内度或出度的节点)。由于地标节点和叶节点的可达性信息在图更新中保持相对稳定,与使用DAG的方法相比,它提供了高效的索引更新机会。因此,DBL建立在两个简单而有效的索引组件之上:(1)动态地标(DL)标签和(2)双向叶(BL)标签。在DBL中结合DL和BL,可以保证有效的索引维护,同时实现具有竞争力的查询处理性能。
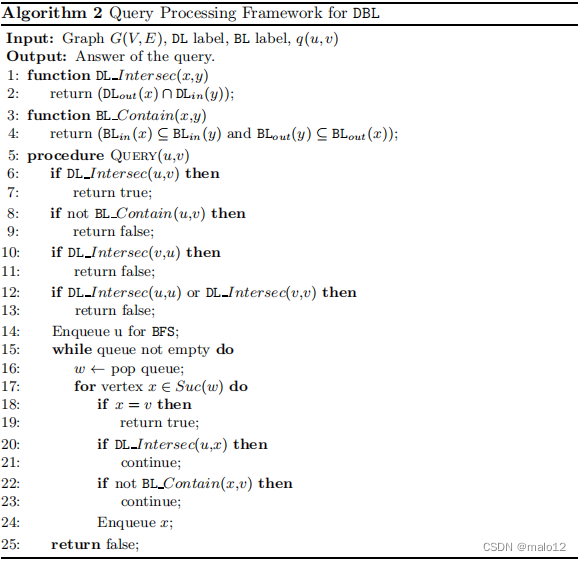
高效的查询处理: DL的灵感来自于地标索引方法[5]。建议的DL标签维护一小部分地标节点作为图中每个顶点的标签。给定一个查询q(u,v),如果u和v的DL标签都包含一个共同的地标节点,我们可以立即确定u到达v。否则,我们需要调用广度优先搜索(BFS)来处理q(u,v)。我们设计了BL标签来快速修剪无法达到的顶点对,以限制昂贵的BFS的数量。BL是对DL的补充,它专注于在图中的叶节点周围构建标签。叶节点形成了一个排他性的集除了地标节点集之外。一个顶点u的BL标签被定义为可以到达u或u可以到达它们的叶节点。因此,如果u的BL标签中存在一个叶节点,而它不出现在v的BL标签中,则u不能到达v。总之,DL可以快速确定可达对,而补充DL的BL可以修剪断开的对来纠正那些DL不能立即确定的对。
有效的索引维护:DL和BL标签都是轻量级索引,其中每个顶点只存储一个恒定大小的标签。当插入新的边时,使用有效修剪的BFS,并且只访问其标签需要更新的顶点。特别是,一旦顶点的标签不受边缘更新的影响,我们就可以安全地从BFS中修剪顶点以及它的后代,从而实现有效的索引更新。
为了更好地利用现代体系结构的计算能力,我们采用简单而紧凑的位操作来实现DL和BL。我们的实现是基于OpenMP和CUDA,以便分别利用并行架构、多核cpu和图形pu(图形处理单元)。
在此,我们将这些贡献总结如下:
我们引入了DBL框架,它结合了两个互补的DL和BL标签,以实现在大型图上高效的可达性查询处理。
我们提出了一种新的针对DL和BL的索引更新算法。据我们所知,这是不保持DAG的动态可达性指数的第一个解决方案。此外,该算法还可以很容易地通过并行接口来实现。
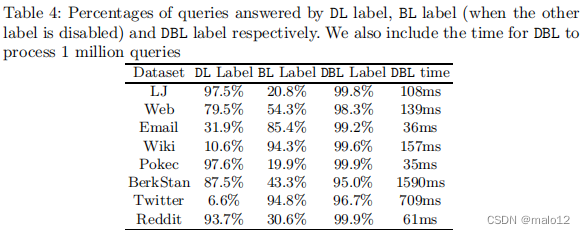
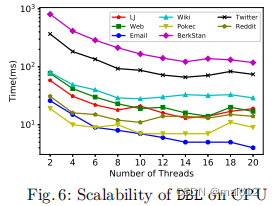
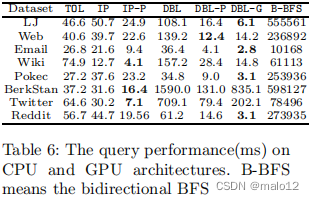
我们进行了大量的实验来验证DBL的性能与最先进的动态方法[27,24]的比较。DBL实现了具有竞争力的查询性能和索引更新的数量级加速。我们还在多核和gpu的系统上实现了DBL,与我们的顺序实现相比,我们展示了显著的性能提高。
本文的其余部分组织如下。第二节介绍了初步工作和背景工作。第3节介绍了相关的工作。第4节介绍了索引定义和查询处理。第5节展示了DL和BL标签的更新机制。第6节报告了实验结果。最后,我们在第7节中总结了论文。
2 Preliminaries
一个有向图被定义为G =(V,E),其中V是顶点集,E是带有n个= |V |和m个= |E|的边集。我们将从顶点u到顶点v的一条边表示为(u,v)。G中从u到v的路径表示为P ath(u,v)= (u,w1,w2,w3,…其中∈和相邻的顶点连接的边缘G我们说v是由u当存在一个P∈(u,v)在G,此外,我们使用子(∈)表示u的直接继承人和u的直接前辈表示为P re (u)。同样地,我们把u(包括u)所有的祖先表示为Anc (u),并且u(包括u)的所有后代为Des (u)。我们将G的反过来的图表示为G‘=(V,E’),其中G的所有边都在G‘的相反方向上。在本文中,正向是指在G‘的边缘上遍历。对称地,反向是指在G’的边缘上遍历。我们将q(u,v)表示为从u到v的可达性查询。本文研究了图中的动态情况。表1总结了常见的符号。
3 Related Work
对动态图[4,6,8,10,15,16,17]有一些研究。Yildirim等人提出匕首[26],在插入和删除后将图保持为DAG。该索引构建在DAG上,以方便可达性查询处理。DAG维护的主要操作是强连接组件(SCC)的合并和拆分。不幸的是,匕首在处理大型图形时(即使顶点只有数百万个[27])的查询处理性能也不理想。
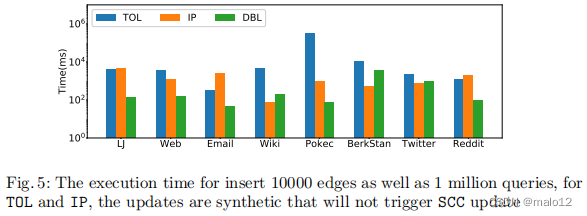
最先进的方法: TOL [27]和IP [24]采用匕首式对DAG的维护方法,在DAG上提出新的动态指标,以提高查询处理性能。我们注意到,TOL和IP只适用于DAG中的SCC/s对更新保持不变的情况。在SCC合并/崩溃的情况下,仍然需要匕首来恢复SCC/s。例如,TOL和IP可以处理图1(a)中的边缘插入(v1、v5),而不需要调用匕首。但是,当插入(v9、v2)时,两个SCC/s {v2}和{v5、v6、v9}将合并为一个较大的SCC {v2、v5、v6、v9}。对于这种情况,TOL和IP首先依赖于匕首来维护DAG,然后执行它们各自的方法来进行索引维护和查询处理。
然而,SCC维护的费用被排除在他们的实验[27,24]中,这样的费用实际上是不可忽视的[26,14]。
在本文中,我们提出了一个DBL框架,它只维护图中所有顶点的标签,而不构造DAG。这意味着,DBL可以有效地避免在图形更新时进行昂贵的DAG维护。DBL通过最先进的解决方案(即TOL和IP)实现了具有竞争力的查询处理性能,同时在索引更新方面提供了数量级的加速。
4 DBL Framework
DBL框架由DL和BL标签组成,它们具有独立的查询和更新组件。在本节中,我们将介绍DL和BL标签。然后,我们设计了一种基于DBL索引的查询处理算法。
4.1 Definitions and Construction
我们提出了由两个索引组件组成的DBL框架: DL和BL。
定义1 (DL标签)。给定一个地标顶点集L⊂V和|L| = k,我们为每个顶点v∈V定义两个标签: DLin (v)和DLout (v)。DLin (v)是L中可以到达v的节点的子集,而DLout (v)是L中v可以到达的节点的子集。
需要注意的是,DL标签是2跳标签[5]的一个子集。事实上,当地标设置为L = V时,DL标签的特殊情况是DL标签。然而,我们发现在动态图场景中保持2-Hop标签会导致索引爆炸。因此,我们建议只选择一个顶点的子集作为地标集L来索引DL标签。这样,DL标签具有高达O(n|L|)的空间复杂度,通过调整L的选择可以很容易地控制索引大小。下面的引理显示了DL标签在可达性查询处理中的一个重要特性。
引理1。给定两个顶点u,v及其对应的DL标签,DLout (u)∩DLin (v) =∅推导出u到达v,但反之亦然。
例子1。我们在图1(a).中展示了一个正在运行的示例假设选择地标集为{v5,v8},对应的DL标签如图1(b).所示q(v1,v10)返回true,因为DLout(v1)∩DLin(v10)= {v8}。然而,尽管有DLout(v3)∩DLin(v11)=∅,但标签还是不能对q(v3,v11)给出否定的答案。这是因为从v3到v11的路径上的中间顶点v7不包括在地标集中。

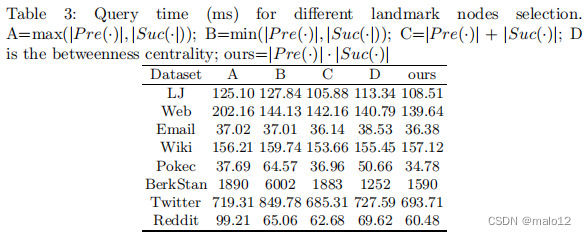
为了实现良好的查询处理性能,我们需要选择一组顶点作为地标,这样它们可以覆盖图中大部分可达顶点对,即DLout(u)∩DLin(v)包含至少一个任意可达顶点对u和v。最优的地标选择已被证明是np硬[13]。本文采用一种启发式的方法来选择DL标签节点。特别地,我们用M (u) = |P re (u)|·|Suc (u)|对顶点进行排序,以近似它们的中心性,并选择前k个顶点。其他的地标选择方法也将在第6.2节中进行讨论。
定义2 (BL标签)。BL为每个顶点v∈V引入了两个标签: BLin (v)和BLout (v)。BLin (v)包含所有可以达到v的零度内顶点,而BLout (v)包含v可以达到的所有零度外顶点。为了方便起见,我们将内度或出度为零的顶点称为叶节点。
引理2。给定两个顶点u,v及其对应的BL标签,如果BLout(v)6⊆BLout (u)或BLin(u)6⊆BLin (v),u不能达到G中的v。
BL标签可以给出q (u、v)的否定答案。这是因为如果你可以达到v,那么你就可以到达v可以到达的所有叶节点,而所有到达u的叶节点也应该达到v。DL标签对于给予可达性查询的积极答案是有效的,而BL标签通过剪枝不可达的对来发挥互补的作用。在本文中,我们以内度/出度为零的顶点作为叶节点。我们还将在第6.2节中讨论其他的叶片选择方法。
例子2。图1©显示了正在运行的示例的BL标签。BL标签对BLin(v6)的回答是否定的,因为BLin(v4)不包含在q(v6)中。直观地说,顶点v1到达顶点v4,但不能到达v6,这说明v4不应该到达v6。BL标签不能给出肯定的答案。以q(v5、v2)为例,标签满足包含条件,但不能给出肯定的答案。
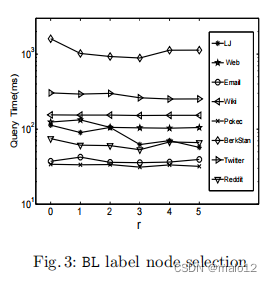
BL标签节点的数量可能会很大。为了开发高效的索引操作,我们为BL构建了一个大小为k‘的哈希集,如下所示。BLin和BLout都是{1,2,……,k‘}的子集,其中k’是用户定义的标签大小,它们存储在位向量中。一个哈希函数用于将叶节点映射到相应的位。对于我们的例子,叶子是{v1、v2、v3、v10、v11}。当k‘=2时,所有的叶子都被散列为两个唯一的值。假设h(v1)= h(v10)= 0,h(v2)= h(v3)= h(v11)= 1。我们在图1©中显示了其中所表示的散列BL标签集如h(BLin)和h(BLout)。在本文的其余部分中,我们直接使用BLin和BLout来表示相应标签的哈希集。值得注意的是,我们仍然可以使用引理2来修剪与散列BL标签不可到达的对。
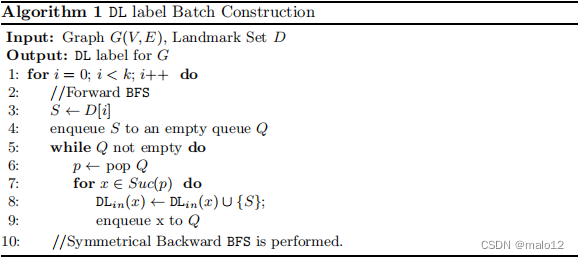
我们简要讨论了DBL的批索引构建,因为本工作的重点是动态场景。算法1提出了DL标签的构造,该算法遵循现有的2跳标签[5]的工作。对于每个地标节点D[i],我们从S(Line 4)开始一个BFS,并在S可以到达的每个顶点(行5-9)的DLin标签中包含S。为了构造DLout,我们在反向图G‘对称执行BFS(第10行)执行BFS。为了构造BL标签,我们只需简单地将地标集D替换为叶集D‘,并将S替换为算法1中散列到桶i(Line 3)的所有叶节点。构建DBL的复杂性是O((k+k‘)(m+n))。
请注意,尽管我们使用[5]来构建离线索引,但我们工作的贡献是,我们将DL和BL作为高效查询处理的补充索引。此外,我们是第一个在不假设SCC/s保持不变的情况下支持高效的动态可达性指数维护的工作。空间复杂性。DL和BL标签的空间复杂度分别为O(kn)和O(k‘n)。