在流行病学研究中,相较于单一因素的暴露,多因素同时暴露的情况更为常见。传统模型在评价多因素联合暴露时存在数据维度高、多重共线性等问题. WQS 回归模型的基本原理是通过分位数间距及加权的方法,将多种研究因素的效应综合成为一个指数,再进行回归分析。不同因素赋予的权重反映了其对结局的影响程度。使用该模型时应满足各研究因素
对结局影响的方向相同这一基本假设.
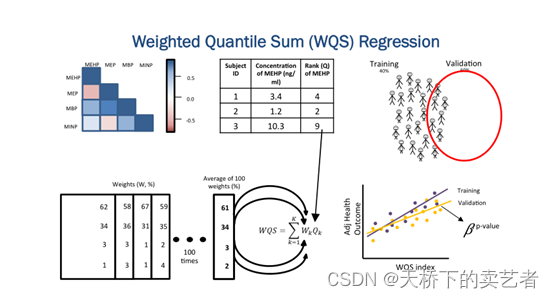
模型的一般形式为:
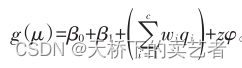
式中:c 表示污染物种类;β 0 表示截距;β 1 表示回归系数,用于限制联合效应对结局影响的方向;w i 表示第 i 种因素的未知权重,取值范围[0,1],且 ∑wi = 1,q i 表示对因素 i 进行 q 分位(如三、四分位等);

上公式表示c 种研究因素的综合权重指数;z 为协变量矩阵,φ为该矩阵的回归系数;g ( )为连接函数,μ 为均数。

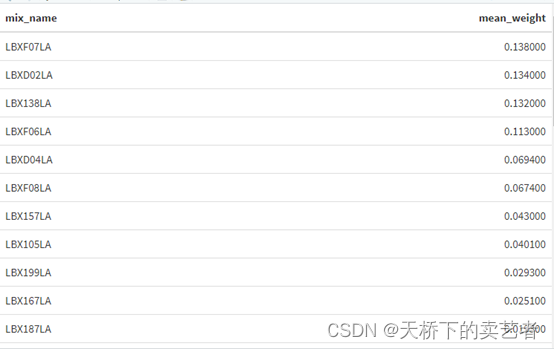
下面咱们来进行演示一下,先导入R包和数据,数据使用的是gWQS自带的数据
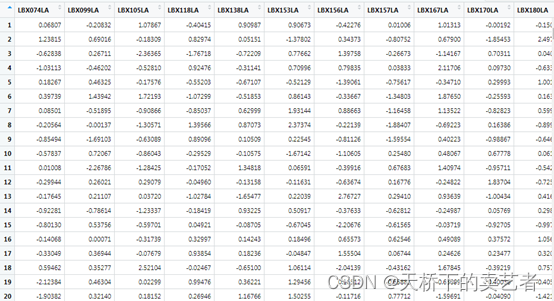
数据挺大的,上图只是数据的一部分,这些数据反映了参与NHANES研究(2001-2002)的受试者中34种多氯联苯暴露和25种邻苯二甲酸酯生物标志物的分布模拟的59种暴露浓度,概括来说就是一些指标的浓度,结局有连续变量和分类变量,还有性别作为协变量。
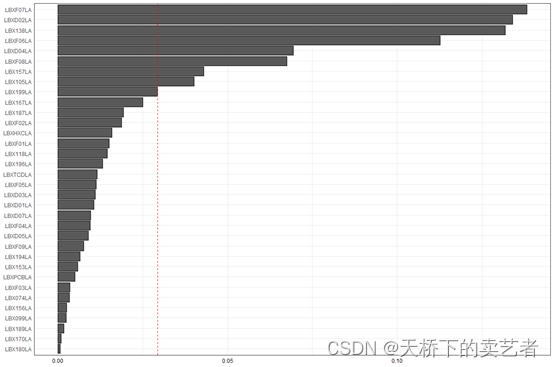
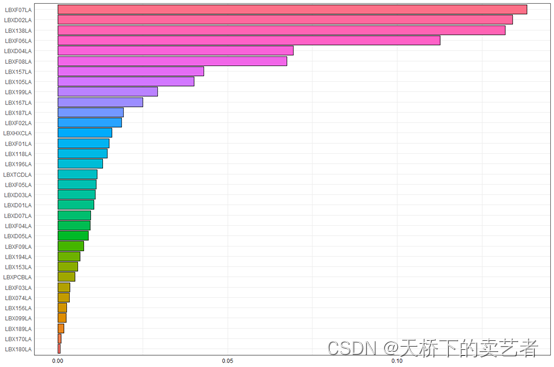
WQS 回归模型的思想就是把指标打包成一个指数,第一步先要确定咱们研究哪些指标,假设咱们研究的是前面34种指标

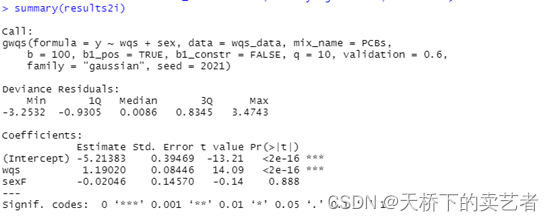
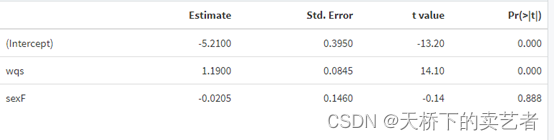
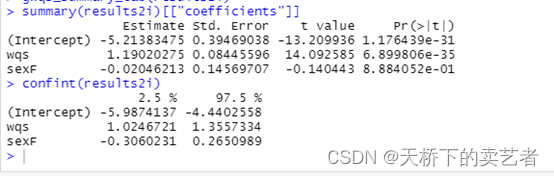
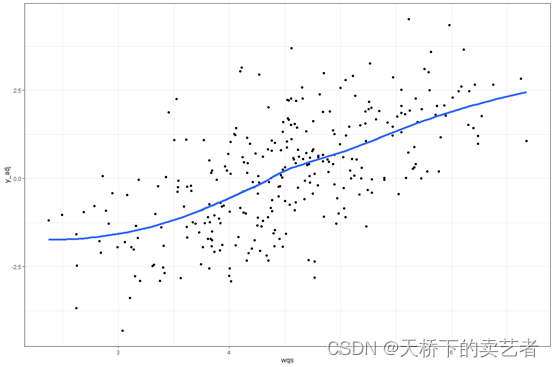
然后就可以生成模型了, 通过 y ~ wqs+sex 将 y 与 34种 PCBs 的联合效应,建立回归方程并调整性别(sex)。其中wqs 是固定参数(即:必须包含项), mix_name=mix 表示指定联合暴露污染物,data =wqs_data 表示输入的数据集为 wqs_data;q=10表示将联合效应进行10分位,在实际运用过程中研究者可设置不同的分位数;validation=0.6 表示随机抽取数据集中的 60% 作为验证集,余下的 40% 作为训练集;b表示 bootstrap 随机抽样次数,该参数至少为 100;b1_pos=TRUE 表示设定联合效应的权重为正 (若为
负则设置为 FALSE);b1_constr=FALSE 表示使用优化算法对权重进行估计时不进行限制(若进行限制则设置为 TURE);family=”gaussian”表示采用高斯分布进行拟合,也可根据研究对象的数据类型采用二项分布、多项式或泊松分布等进行拟合;由于涉及 boot⁃strap 随机抽样过程,将随机种子数 (seed) 设置为2021。