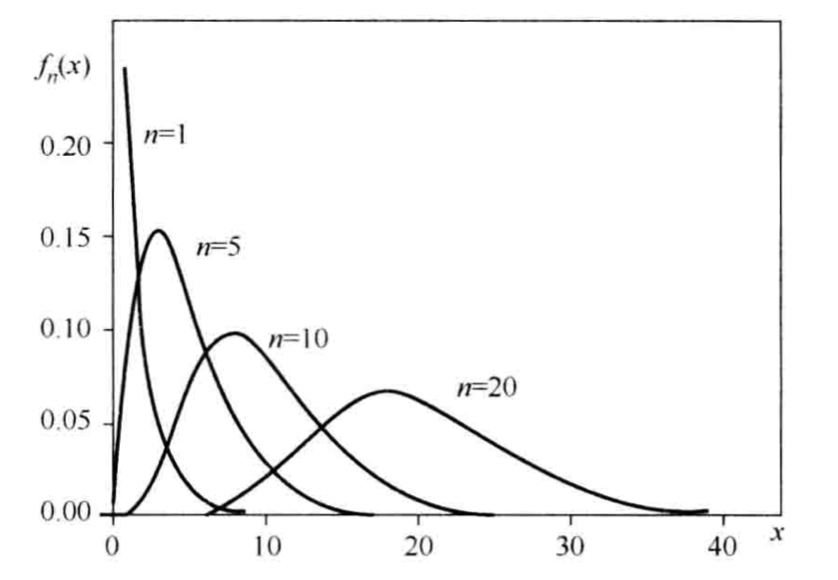
X称为自由度为
n
n
n的
F
F
F分布:设
X
∼
χ
2
(
n
1
)
X∼χ2(n1),
Y
∼
χ
2
(
n
2
)
Y∼χ2(n2),且
X
X
X与
Y
Y
F
=
X
/
n
1
Y
/
n
2
F = frac{X / n_1}{Y / n_2}
F=Y/n2X/n1称为自由度为
(
n
1
,
n
2
)
(n_1, n_2)
(n1,n2)的
F
F
F分布,记作
F
∼
F
(
n
1
,
n
2
)
F sim F(n_1, n_2)
X称为自由度为
n
n
n的
t分布,记作
T
∼
(
n
)
T∼t(n)。
t
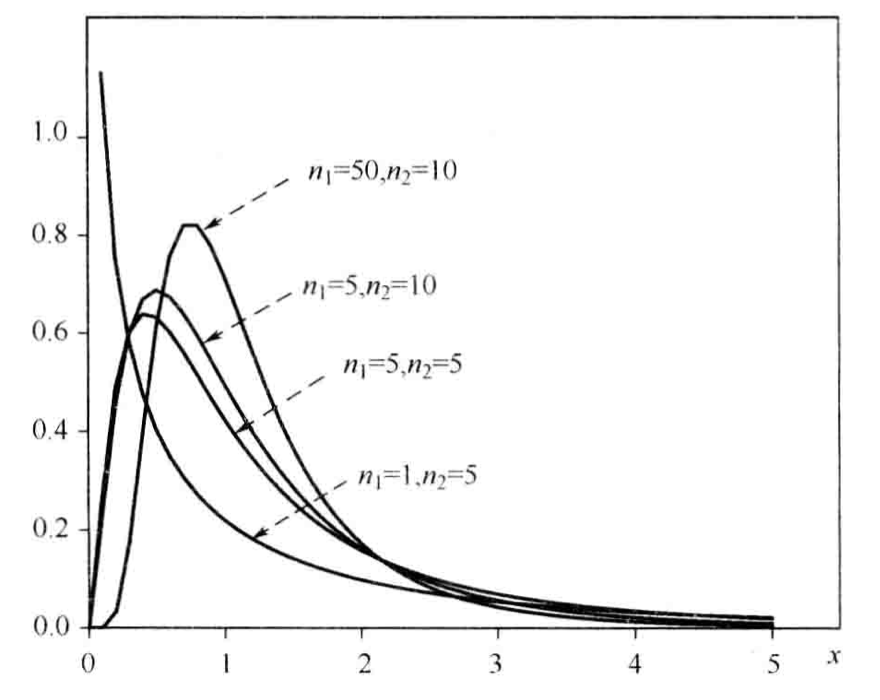
F
F
F分布:设
X
∼
χ
2
(
n
1
)
X∼χ2(n1),
Y
∼
χ
2
(
n
2
)
Y∼χ2(n2),且
X
X
X与
Y
Y
F
=
X
/
n
1
Y
/
n
2
F = frac{X / n_1}{Y / n_2}
F=Y/n2X/n1称为自由度为
(
n
1
,
n
2
)
(n_1, n_2)
(n1,n2)的
F
F
F分布,记作
F
∼
F
(
n
1
,
n
2
)
F sim F(n_1, n_2)

这三个分布有什么用呢?
分布:在信息不足的情况下,要对总体均值进行估计和检验,就会使用到
P
(
A
∩
B
)
P(A∩B)。
P
(
A
∣
B
)
Ω
P
(
B
)
>
0
P(B)>0。那么在事件B发生的条件下,事件A发生的条件概率为:
P
(
A
∣
B
)
=
P
(
A
∩
B
)
P
(
B
)
{P(A|B)=frac{P(A cap B)}{P(B)}}
P(A∣B)=P(B)P(A∩B),当$ P(B)=0
时,规定
时,规定
时,规定 P(A|B) = 0 $。
思考:
事件A在事件B已发生的条件下发生的概率,与事件B在事件A已发生的条件下发生的概率是不一样的。然而,这两者是有确定的关系的,贝叶斯定理就是对这种关系的陈述,如下所示:
P
(
A
∣
B
)
=
P
(
B
∣
A
)
P
(
B
)
P
(
A
)
P(A|B)=frac{P(B|A)}{P(B)}P(A)
P(A∣B)=P(B)P(B∣A)P(A)
P
(
A
∣
B
)
P(A|B)
P(A∣B)是已知
B
B
B发生后,
A
A
A的条件概率,也称为
A
A
A的后验概率。
P
(
A
)
P(A)
P(A)是
A
A
A的先验概率也称作边缘概率,是不考虑
B
B
B时
A
A
A发生的概率。
P
(
B
∣
A
)
P(B|A)
P(B∣A)是已知
A
A
A发生后,
B
B
B的条件概率,称为
B
B
B的似然性。
P
(
B
)
P(B)
P(B)是
B
B
B的先验概率。
ϵ
ϵ,有:
lim
n
→
∞
P
(
∣
X
n
ˉ
−
μ
∣
>
ϵ
)
=
0
lim_{n to infty}P(|bar{X_n}-mu|>epsilon)=0
limn→∞P(∣Xnˉ−μ∣>ϵ)=0。
P
(
lim
n
→
∞
X
n
ˉ
=
μ
)
=
1
P(lim_{n to infty}bar{X_n}=mu)=1
P(limn→∞Xnˉ=μ)=1。
假设检验就是通过抽取样本数据,并且通过小概率反证法去验证整体情况的方法。假设检验的核心思想是小概率反证法(首先假设想推翻的命题是成立的,然后试图找出矛盾,找出不合理的地方来证明命题为假命题),即在零假设(通常记为
H
0
H_0
H0)的前提下,估算某事件发生的可能性,如果该事件是小概率事件,在一次试验中本不应该发生,但现在却发生了,此时我们就有足够的理由怀疑零假设,转而接受备择假设(通常记为
H
A
H_A
HA)。
假设检验会存在两种错误情况,一种称为“拒真”,一种称为“取伪”。如果原假设是对的,但你拒绝了原假设,这种错误就叫作“拒真”,这个错误的概率也叫作显著性水平
α
α,或称为容忍度;如果原假设是错的,但你承认了原假设,这种错误就叫作“取伪”,这个错误的概率我们记为
β
β。
描述性统计通常用于研究表象,将现象用数据的方式描述出来(用整体的数据来描述整体的特征);推理性统计通常用于推测本质(通过样本数据特征去推理总体数据特征),也就是你看到的表象的东西有多大概率符合你对隐藏在表象后的本质的猜测。
原文地址:https://blog.csdn.net/ml202187/article/details/134704386
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_10525.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!