[PyTorch][chapter 2][李宏毅深度学习-Regression]

本文介绍: torch.opt i m.SGD是PyTorch中实现的Stoch a s t ic Grad ient Des cent(SGD)优化器，用于更新神经网络中的参数，以最小化损失函数，从而提高模型的精度。- we i g ht_d ecay：权重衰减（we i g ht d e cay），也称权重衰减（we i ght re g ul ar izati on），用于防止过拟合。一些常见情况时，如上次梯度过大，导致进入局部最小点时，下一次更新能很容易借助上次的大梯度跳出局部最小点。- lr：学习率（le arnin g rate），控制每次参数更新的步长。

前言：

Re g res s ion 模型主要用于股票预测,自动驾驶,推荐系统等领域.

这个模型的输出是一个 scalar。这里主要以下一个线性模型为基础

它是神经网络的基础模块，

总体流程
常见问题
Num py 例子
PyTorch 例子

一总体流程

1 : 建模(model)

$y=w^Tx+b$

$=sum_{i}w_ix_i+b$

其中： w: weight权重系数向量

b：bi a s 偏置系数 scalar

x：输入数据向量

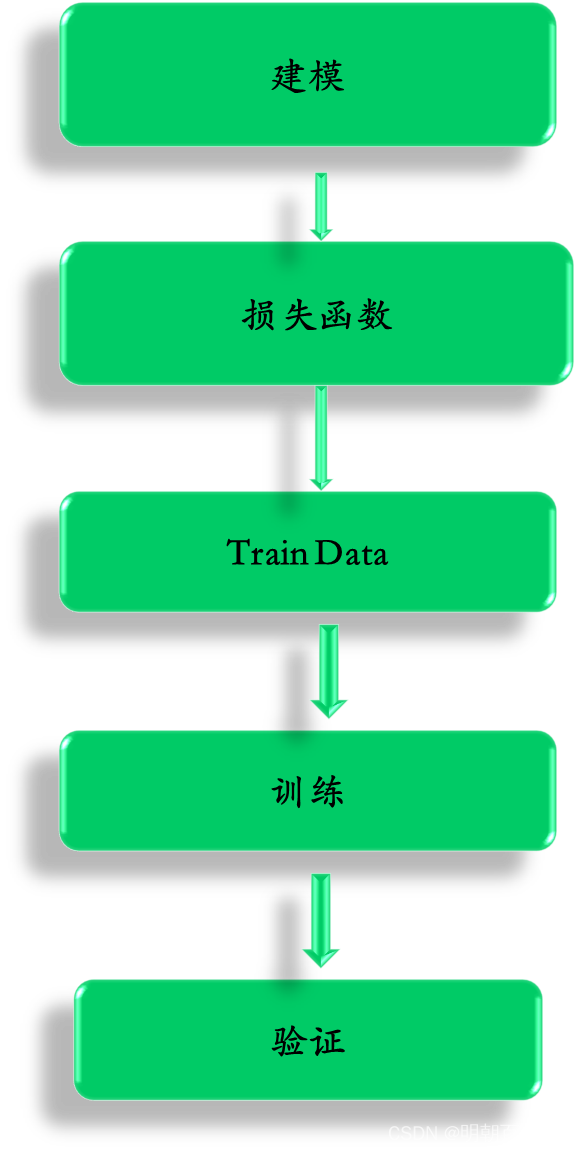
2： TrainData

收集N个样本，其中

$hat{y}$ : 标签 target

$x:$ [n,1]的列向量

$x^i,hat{y}^{i}$ : 一组训练数据

数据集如下：

$begin{bmatrix} (x^1,hat{y}^1)\ (x^2,hat{y}^2) \ .... \ (x^N,hat{y}^N) \ end{bmatrix}$

3：损失函数

用来度量Goodnes s of Function，一般用MSE loss

$L(w.b)=sum_{n=1}^{N}(hat{y}^{n}-(w^Tx^n+b))^2$

我们训练的目标是找到最优的参数w,b使得loss 最小

$w^{*},b^{*}=argminL_{w,b}(w,b)$

4: 训练

训练的时候,主要通过梯度下降方法 Grad ient Des cent

二常见问题

2.1 Grad ient Discent 局部极小值问题

当损失函数是非凸函数，可能有多个局部极小点.如下图

如上图，当梯度为0 的时候，此刻参数就无法更新了，导致

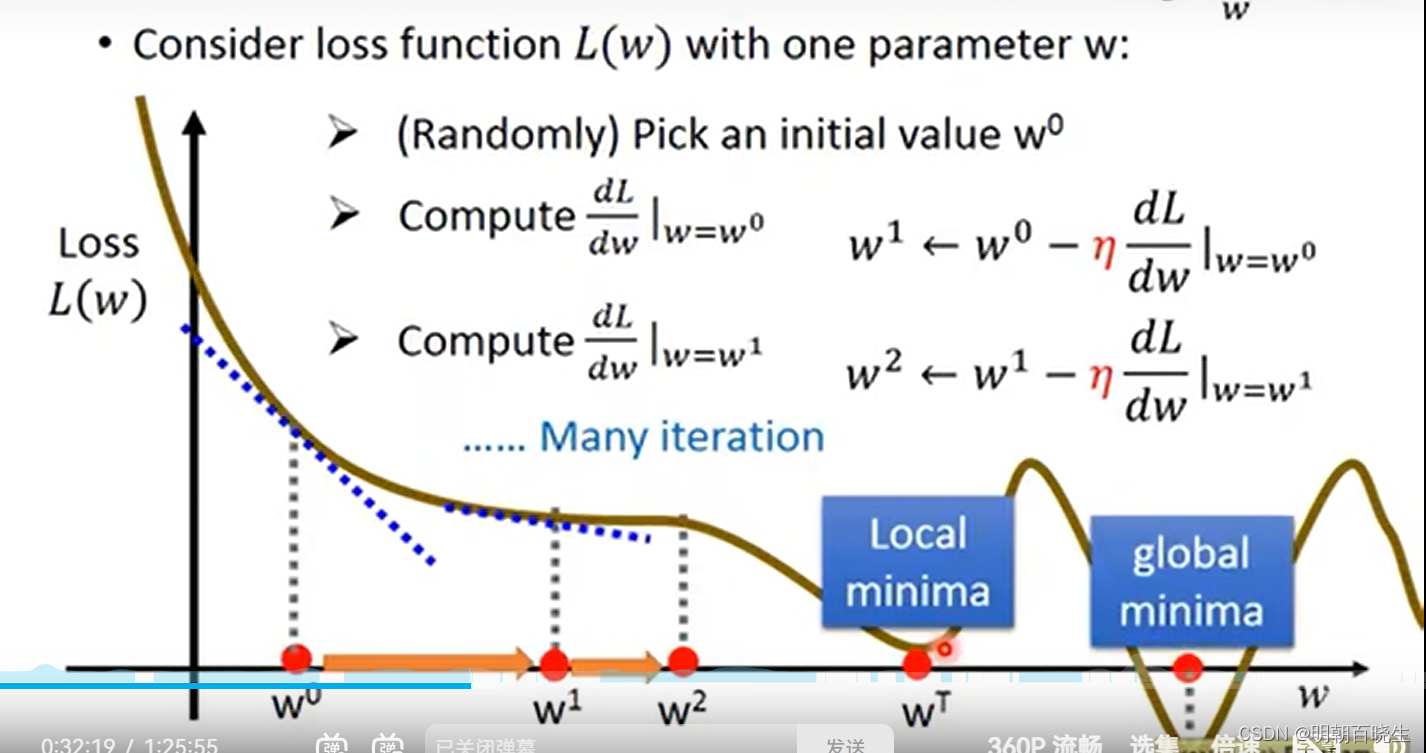
loss 陷入了局部极小值点，无法更新到全局最小值点.当多维参数的时候

在sad dle point 陷入到局部极小值点.

解决方案：

Adagrad: 自适应学习率,会根据之前的梯度信息自动调整每个参数的学习率。
RMSprop: 自适应学习率,根据历史梯度信息,采用了指数加权移动平均,
stochastic GD: 其每次都只使用一个样本进行参数更新，这样更新次数大大增加也就不容易陷入局部最优
Mini-Batch GD: 每次更新使用一小批样本进行参数更新
每次更新前加入部分上一次的梯度量，这样整个梯度方向就不容易过于随机。
一些常见情况时，如上次梯度过大，导致进入局部最小点时，下一次更新能很容易借助上次的大梯度跳出局部最小点。

2.2 过拟合问题

如上图, 五个拟合函数。函数5最复杂，在Training 数据集上的loss 最小

但是在Testing 数据集上 loss 最大,这种称为过拟合.

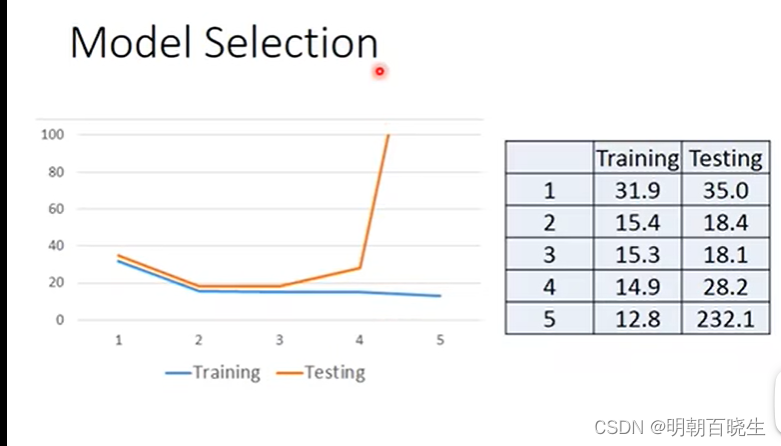
解决方案：

在Training Data 收集更多的数据集

L2 正规化

三 Numpy 代码例子

# -*- coding: utf-8 -*-
"""
Created on Tue Nov 28 16:19:48 2023

@author: chengxf2
"""

# -*- coding: utf-8 -*-
"""
Created on Tue Nov 28 14:47:32 2023

@author: chengxf2
"""

import numpy as np
import matplotlib.pyplot as plt




def load_trainData():
    
    x_data =[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    y_data =[3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
    
    #y_data = b+w*xdata 
    return x_data, y_data


def draw(x_data,y_data,b_history, w_history):
    #plot the figure
    #x = np.arange(-200, -100, 1.0) #bias
    
    x = np.arange(-5, 5, 0.1) #bias
    y = np.arange(-10, 10, 0.1) #weight
    Z = np.zeros((len(y),len(x))) #ndarray
    X, Y = np.meshgrid(x,y)
    print("n-----z ---",Z.shape)

    for i in range(len(x)):#100
        for j in range(len(y)):#40
            w = x[i]
            b = y[j]
            #print(j,i)
            Z[j,i]=0
            for n in range(len(x_data)):
                Z[j,i]=Z[j,i]+(y_data[n] -b-w*x_data[n])**2
                
            Z[j,i]== Z[j,i]/len(x_data)
   
    #绘制等高线,cmp = plt.get_cmap('jet')
   
    plt.contourf(x,y,Z, 50, alpha = 0.5, cmap='rainbow')
    plt.plot([1.0], [2.0], 'x', ms=10, markeredgewidth =30, color ='red')
    
    plt.plot(w_history, b_history, 'o-', ms=3, lw =5, color ='green')
    plt.xlim(-10, 10)
    plt.ylim(-10, 10)
    plt.xlabel(r'$b$',fontsize =16)
    plt.ylabel(r'$w$',fontsize =16)
    plt.show()
            
                


class regression():
    
    
    def learn(self,x_data,y_data):
        
        N = len(x_data)
        b_history = []
        w_history = []
        for i in range(self.iteration): 
            w_grad = 0.0
            b_grad = 0.0
            
            for n in range(N):
                w_grad = w_grad +2.0*(self.b+self.w*x_data[n]-y_data[n])*x_data[n]
                b_grad = b_grad +2.0*(self.b+self.w*x_data[n]-y_data[n])*1.0
                
               
            self.b = self.b -self.lr*b_grad
            self.w = self.w- self.lr*w_grad
            
            b_history.append(self.b)
            w_history.append(self.w)
        print("n 偏置: ",round(self.b,1), "n 权重系数 ",round(self.w,1))
        return w_history,b_history
            
        
        
        
    
    
    def initPara(self):
        
        self.b = -120 #initial b
        self.w = -4.0 #initial w
        self.lr = 1e-3 #learning rate
        self.iteration = 10000 #iteration Number
        
    
    
    def __init__(self):
        
        
        self.b = 0 
        self.w = 0
        self.lr = 0
        self.iteration = 0
        
        

if __name__ == "__main__":
    
    
    model = regression()
    x_data,y_data = load_trainData()
    
    model.initPara()
    w_history,b_history = model.learn(x_data, y_data)
    draw(x_data,y_data,b_history, w_history)

四 PyTorch API 例子

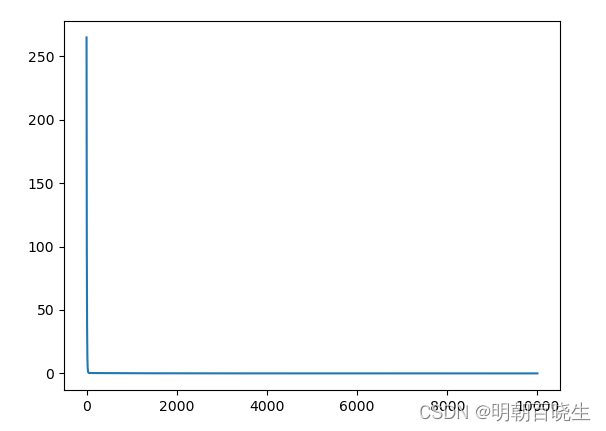
loss 情况

torch.optim.SGD是PyTorch中实现的Stochastic Gradient Descent(SGD)优化器，用于更新神经网络中的参数，以最小化损失函数，从而提高模型的精度。它的一些重要参数如下：

– lr：学习率（learning rate），控制每次参数更新的步长。默认值为0.001。
– momentum：动量（momentum），加速SGD在相关方向上前进，抑制震荡。常常取值为0.9。若设为0，则为经典的SGD算法。
– dampening：阻尼（dampening），用于防止动量的发散。默认值为0。
– weight_decay：权重衰减（weight decay），也称权重衰减（weight regularization），用于防止过拟合。默认值为0。
– nesterov：采用Nesterov加速梯度法（Nesterov ac celerated gradient，NAG）。默认值为False

# -*- coding: utf-8 -*-
"""
Created on Tue Nov 28 16:27:30 2023

@author: chengxf2
"""



import torch
import numpy as np
import matplotlib.pyplot as plt
from torchsummary import summary


#加载PyTorch数据集
def load_data():
    x_data =[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    y_data =[3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
    x = torch.Tensor(x_data)   #将列表a转成tensor类型
    one = torch.ones_like(x)
    Y = torch.Tensor(y_data)  
    X = torch.stack([x,one],dim=1)
    
    return  X,Y.view(10,1)

#建模
class NN(torch.nn.Module):
    
    def __init__(self, xDim, yDim):
        super(NN,self).__init__()
        self.predict = torch.nn.Linear(xDim, yDim,bias=False)
        
    def forward(self, x):
        y = self.predict(x)
        return y
    

#训练
def learn(X,Y):
    #X 数据集 Y 标签集

    model = NN(2,1)
    optimizer = torch.optim.SGD(model.parameters(),lr=0.001)  #优化方法为随机梯度下降
    loss_f = torch.nn.MSELoss()
    
    lossHistory =[]

    for i in range(10000):

         predict = model(X)
         loss = loss_f(predict, Y)
         #print("n loss ",loss.item())
         lossHistory.append(loss.item())
         optimizer.zero_grad()
         loss.backward()
         optimizer.step()

     #y_predict = y_predict.detach().numpy()
    N = len(lossHistory)
    x = np.arange(0, N)
    plt.plot(x, lossHistory)
    summary(model, input_size=(1,2), batch_size=-1)
    for param in model.parameters():
        print("n 参数 ",param)



    

 

        


if __name__ == "__main__":
    
  x,y = load_data() 
  learn(x,y )

参考：

sam+yolov8

1 [2023] 李宏毅机器学习完整课程 43
https://www.bi libili.com/video/BV1NX4y1r7nP/?spm_id_from=333.337.search-card.all.click&vd_source=a624c4a1aea4b867c580cc82f03c1745

2 【2022】最新李宏毅大佬的深度学习与机器学 P90

https://www.bi libili.com/video/BV1J94y1f7u5/?spm_id_from=333.337.search-card.all.click&vd_source=a624c4a1aea4b867c580cc82f03c1745

3 [2020 ]李宏毅机器学习深度学习(完整版)国语 P119

https://www.bilibili.com/video/BV1JE411g7XF/?spm_id_from=333.337.search-card.all.click&vd_source=a624c4a1aea4b867c580cc82f03c1745

4 [2017 ]李宏毅机器学习 P40

https://www.bilibili.com/v ideo/BV13x411v7US/?spm_id_from=333.337.search-card.all.click&vd_source=a624c4a1aea4b867c580cc82f03c1745

5 李宏毅: 强化学习 P11

https://www.bilibili.com/v ideo/BV1XP4y1d7Bk/?spm_id_from=333.337.search-card.all.click&vd_source=a624c4a1aea4b867c580cc82f03c1745
————————————————
版权声明：本文为CSDN博主「明朝百晓生」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/chengxf2/art icle/details/134643845