7-1 这是一道送分题
为了让更多的同学参与程序设计中来,这里给同学们一个送分题,让各位感受一下程序设计的魅力,并祝贺各位同学在本次比赛中取得好成绩。
注:各位同学只需将输入样例里的代码复制到右侧编译器,然后直接提交即可。
输入格式:
无。
输出格式:
无。
输入样例:
#include<bits/stdc++.h>
using namespace std;
int main(){
int i,j,k,l,m;
char c='/*';
cout<<endl;
for (i=1;i<=3;i++){
for (j=1;j<=32-2*i;j++)
cout<<" ";
for (k=1;k<=4*i+1;k++)
cout<<c;
for (l=1;l<=13-4*i;l++)
cout<<" ";
for (m=1;m<=4*i+1;m++)
cout<<c;
cout<<endl;
}
for (i=1;i<=3;i++){
for (j=1;j<=24+1;j++)
cout<<" ";
for (k=1;k<=29;k++)
cout<<c;
cout<<endl;
}
for (i=7;i>=1;i--){
for (j=1;j<=40-2*i;j++)
cout<<" ";
for (k=1;k<=4*i-1;k++)
cout<<c;
cout<<endl;
}
for (i=1;i<=39;i++)
cout<<" ";
cout<<c<<endl;
return 0;
}
输出样例:
这里为输入样例的代码运行出来的结果,不嫌麻烦的同学也可以使用printf对下面的结果一行一行去输出。
***** *****
********* *********
************* *************
*****************************
*****************************
*****************************
***************************
***********************
*******************
***************
***********
*******
***
*
#include<bits/stdc++.h>
using namespace std;
int main(){
int i,j,k,l,m;
char c='/*';
cout<<endl;
for (i=1;i<=3;i++){
for (j=1;j<=32-2*i;j++)
cout<<" ";
for (k=1;k<=4*i+1;k++)
cout<<c;
for (l=1;l<=13-4*i;l++)
cout<<" ";
for (m=1;m<=4*i+1;m++)
cout<<c;
cout<<endl;
}
for (i=1;i<=3;i++){
for (j=1;j<=24+1;j++)
cout<<" ";
for (k=1;k<=29;k++)
cout<<c;
cout<<endl;
}
for (i=7;i>=1;i--){
for (j=1;j<=40-2*i;j++)
cout<<" ";
for (k=1;k<=4*i-1;k++)
cout<<c;
cout<<endl;
}
for (i=1;i<=39;i++)
cout<<" ";
cout<<c<<endl;
return 0;
}7-2 求一元二次方程
输入格式:
无
输出格式:
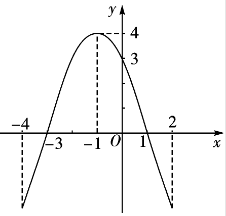
注:本题作者已经给你求出a和b的结果,请通过看图得到c的值,并完成正确结果的输出。
输入样例:
在这里给出一组输入。例如:
无
输出样例:
在这里给出相应的输出。例如:
a=-1,b=-2,c=0#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<"a=-1,b=-2,c=3";
return 0;
}7-3 求积分
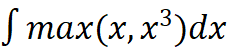
输入格式:
输出格式:
保留两位小数输出结果。
输入样例:
在这里给出一组输入。例如:
2
输出样例:
在这里给出相应的输出。例如:
4.00#include<bits/stdc++.h>
using namespace std;
int main(){
double x,y=0;
cin>>x;
if(x>1||(x>-1&&x<0))y=pow(x,4)/4;
else y=pow(x,2)/2;
printf("%.2f",y);
return 0;
} #include<bits/stdc++.h>
using namespace std;
int main(){
double x,z,y=0;
cin>>x;
z=x*x*x;
if(x<z)y=pow(x,4)/4;
else y=pow(x,2)/2;
printf("%.2f",y);
return 0;
} 7-4 小袁的X
小袁想出一道循环输出图形,然后他看到了X,请各位同学告诉他应该怎么输出。
输入格式:
输入一个整数n。
输出格式:
输出一个有n行的“X”型图形。
输入样例1:
在这里给出一组输入。例如:
3
输出样例1:
在这里给出相应的输出。例如:
* *
*
* *
输入样例2:
在这里给出一组输入。例如:
4
输出样例2:
在这里给出相应的输出。例如:
* *
**
**
* *#include<bits/stdc++.h>
using namespace std;
int main(){
int a;
cin>>a;
for(int i=1;i<=a;i++)
{
for(int j=a;j>=1;j--)
{
if((i+j==a+1)||(i==j)) printf("*");
else printf(" ");
}
printf("n");
}
return 0;
}你了解回文串嘛?简单来说回文串指正读和反读都是一样的字符串。例如:“abba”是一个回文串,“abca”则不是。现在我们需要对回文串进行一个“简单”操作,我相信每个同学都能够做到。
操作:你需要做的操作是在一串N长度的字符串中删除K个字符,任意排列此字符串能否使它成为回文串,如果能输出YES,不能输出NO。
输入格式:
第一行给出T(T < 100)组测试数据。
接下来每组测试输入一个N(1 <= N <= 1e5)和 K(0 <=k <= N)。
下一行输入一个长度为N的字符串进行上述操作。
输出格式:
按照样例即可。
输入样例1:
1
1 0
b
输出样例1:
在这里给出相应的输出。例如:
YES
输入样例2:
10
1 0
a
2 0
ab
2 1
ba
3 1
abb
3 2
abc
6 2
bacacd
6 2
fagbza
6 2
zwaafa
7 2
taagaak
14 3
ttrraakkttoorr
输出样例1:
在这里给出相应的输出。例如:
YES
NO
YES
YES
YES
YES
NO
NO
YES
YES#include<bits/stdc++.h>
using i64 = long long;
using u64 = unsigned long long;
#define IOS std::ios::sync_with_stdio(false), std::cin.tie(nullptr), std::cout.tie(nullptr)
#define all(v) (v).begin(),(v).end()
void debug(std::vector <int> &a, int n){for (int i = 1; i <= n; i ++){std::cout << a[i] << " n"[i == n];}}
void YES(){std::cout << "YESn";}
void NO(){std::cout << "NOn";}
void Yes(){std::cout << "Yesn";}
void No(){std::cout << "Non";}
void yes(){std::cout << "yesn";}
void no(){std::cout << "non";}
const int N = 2e5 + 10;
constexpr i64 mod1 = 998244353, mod2 = 1e9 + 7;
//先独自构造出一个回文串看需要的是否满足,然后有单的尽量再放一个进去,与需要的字符个数进行判断即可
void solve(){
int n, k;
std::string s;
std::cin >> n >> k >> s;
if (n - k == 1){
YES();
return ;
}
std::map <char, int> mp;
int need = n - k;
for (auto x : s){
mp[x] ++;
}
int ans = 0, dan = 0;
for (auto [x, y] : mp){
ans += y / 2;
if (y % 2){
dan ++;
}
}
int res = ans * 2 + (dan > 0 ? 1 : 0);
if (res >= need){
YES();
}else {
NO();
}
}
int main()
{
IOS;
int _;
std::cin >> _;
while (_ --) solve();
return 0;
}7-6 钟离的尘世一日闲游
海灯节快到了,往生堂陆陆续续开始组织员工们进行休假,今天就轮到了钟离。对这种难得一次的休假,钟离已经做好了尘世闲游的规划,当假期批准时就踏上了旅程。在路经石门时,他发现这次出门又没有带摩拉,而石门距离邻国蒙德已经不远了,于是钟离决定去蒙德寻找温迪帮忙。由于两国之间还存在多条关口路径,且只能够经由若干个关口路经才可能到达蒙德,钟离想知道这些关口之间是不是互相连通的,以便他判断是否可以从任意关口出发最终都可以到达蒙德,现在已知两地之间共有N个关口(关口从1—N编号),这些关口之间存在M条关口路径。想请你设计程序,帮助钟离判断这些关口是不是互相连通的。
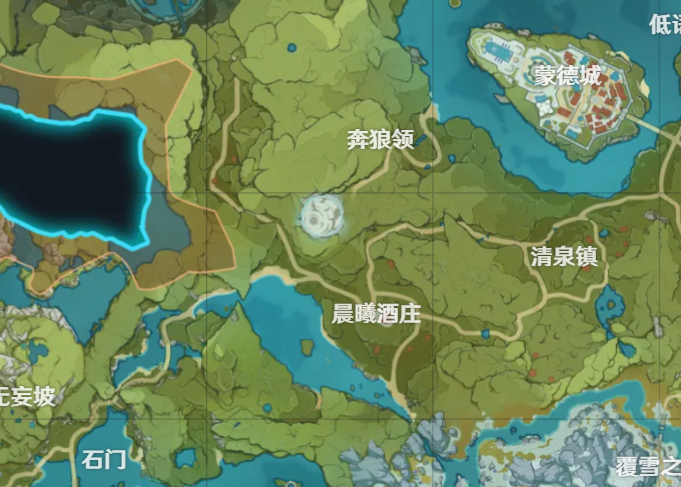
输入格式:
第一行输入一个正整数N和正整数M(1<=N<=10,0<=M<=10)。
接下来M行,每行输入三个正整数R1,R2(1<=R1,R2<=M),表示关口R1与关口R2之间存在一条关口路经。
输出格式:
如果所有关口都是连通的,那么输出一行”Accept”(引号不输出)。
如果所有关口并不是连通的,那么在一行中输出一个整数S,代表这些关口组成的集合数。
这里给出关口集合的定义:连通的多个关口(也可以只有一个关口)被称为一个关口集合。
比如:
(1)一共有3个关口,其中关口1、2、3是连通的,那么称关口1、2、3是一个关口集合;
(2)一共有3个关口,其中仅关口1、2是连通的,那么称关口1、2是一个关口集合,关口3单独也是一个关口集合。
注:关口集合的子集不能够作为一个关口集合。
输入样例:
4 3
1 2
2 3
1 3
输出样例:
2#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
using namespace std;
const int MAX=15;
//最大路经数
int p[MAX];
//并查集根节点数组
int find(int);
//建立并查集函数
int main(void){
IOS;
int N, M;
cin>>N>>M;
for(int i=1;i<=N;i++) //初始化并查集根节点数组,初始时各个关口节点互不相关
p[i]=i;
for(int i=0;i<M;i++){ //输入N个关口路经连通关系
int R1, R2;
cin>>R1>>R2;
p[find(R1)]=find(p[R2]); //合并关口节点
}
int cnt=0;
for(int i=1;i<=N;i++)
if(p[i]==i) cnt++; //对并查集中的集合数计数
if(cnt==1)
//如果集合数为1,说明其中所有结点都是连通的
cout<<"Acceptn";
else
//否则不连通,输出集合的个数
cout<<cnt<<endl;
return 0;
}
int find(int x){
if(x!=p[x]) return find(p[x]);
return p[x];
}任意输入一个n阶矩阵,将该矩阵旋转 r*90° 后输出。当 r < 0 时逆时针旋转,当 r > 0 时顺时针旋转。例如,当 r = -1 时逆时针旋转90°,当 r = 2 时顺时针旋转180°。
输入格式:
第一行输入两个整数 n 和 r( 1 ≤ n ≤ 1000,-1000 ≤ r ≤ 1000) 。
输出格式:
输入样例:
在这里给出一组输入。例如:
3 1
1 2 3
4 5 6
7 8 9
输出样例:
在这里给出相应的输出。例如:
7 4 1
8 5 2
9 6 3#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int a[N][N], n, r;
void rotate(int r);
int main()
{
cin >> n >> r;
for(int i = 0; i < n; i ++)
for(int j = 0; j < n; j ++)
cin >> a[i][j];
if(r < 0) r = (-r)%4==0 ? 0 : 4 - (-r)%4; // 求补数
else r = r % 4; //求余数
rotate( r );
return 0;
}
void rotate(int r)
{
if(r == 0) { // 旋转0°
for(int i = 0; i < n; i ++) {
for(int j = 0; j < n; j ++) {
if(j != 0) cout << " ";
cout << a[i][j];
}
cout << endl;
}
} else if(r == 1) { // 旋转90°
for(int j = 0; j < n; j ++) {
for(int i = n - 1; i >= 0; i --) {
if(i != n - 1) cout << " ";
cout << a[i][j];
}
cout << endl;
}
} else if(r == 2) { // 旋转180°
for(int i = n - 1; i >= 0; i --) {
for(int j = n - 1; j >= 0; j --) {
if(j != n - 1) cout << " ";
cout << a[i][j];
}
cout << endl;
}
} else if(r == 3) { // 旋转270°
for(int j = n - 1; j >= 0; j --) {
for(int i = 0; i < n; i ++) {
if(i != 0) cout << " ";
cout << a[i][j];
}
cout << endl;
}
}
}7-8 我只想要分
完全赛题目由N个部分组成,每个部分有两个题,分别是A类题和B类题,答题者可从两道题中选一道题作答,两题分数可能不同
现有一位完全AC大佬,对于完全AC大佬的解释我们可以理解为对大佬来说,所有题都是送分题,我们只需要帮助大佬算出他所能取得的最高分数
注意:机制要求最终答题者所选的A类题和B类题题数之差不得大于1
输入格式:
接下来N行每行给出两个正实数,分别为该部分A类题与B类题的分数
输出格式:
输出该场完全赛大佬在合规的情况下所能取得的最高分数,分数要求保留两位小数输出
输入样例:
在这里给出一组输入。例如:
5
2 3
8.05 4
25 24
89 68
25 23
输出样例:
在这里给出相应的输出。例如:
149.05
样例中我们把第2、4、5部分选A类,第1、3部分选B类,结果为3+8.05+24+89+25=149.05
#include<bits/stdc++.h>
using namespace std;
double a,b[10001];
bool com(double a,double b){
return a>b;
}
int main(){
int n;
double sum;
cin>>n;
if(n==0){
cout<<"0.00";
return 0;
}
for(int i=0;i<n;i++){
cin>>a>>b[i];
b[i]=b[i]-a;
sum+=a;
}
sort(b,b+n,com);
for(int i=0;i<n/2;i++){
sum+=b[i];
}
if(n%2){
sum=max(sum,sum+b[n/2]);
}
printf("%.2lf",sum);
return 0;
} 水神不歪^_^
在提瓦特大陆上总是能够遇见许多元素方碑,这不,孙俊豪带着纳西妲在须弥的雨林里散步时就发现有一处草方碑的解密,走近一看发现是N个元素方碑的排列解密问题,必须要按照固定的排列顺序激活方碑才可以完成这个解密,由于孙俊豪没有看攻略的习惯,他就决定自己动手解密,他打算拿出草稿本写出所有可能的排列,然后一一进行测试,但是人工计算排列的时间成本实在太高了,所以还得交给计算机来实现。由于孙俊豪是个混子,学艺不精,设计不出这种程序,于是现在他想请你帮忙,设计出这样一个程序,帮助他成功解密拿到原石。

N个元素方碑从左到右依次线性排列,依次编号为1-N(2 <= N <= 10),并且每一个方碑都有其对应的基础权值(权值依次为999,9999,99999,.…..)。当元素方碑被点亮时,它对应的实际权值=i×基础权值,其中i代表该元素方碑是第i个被点亮的。最终点亮全部方碑时,系统会计算出全部方碑的实际权值和,以此做出判断。
解密成功的条件是:
当N个元素方碑都被点亮并且它们实际权值的合等于Q。
注:每一个元素方碑只能被点亮一次。
样例1解释:
第一次点亮编号为2的方碑,此时它的实际权值为1*9999=9999
第二次点亮编号为3的方碑,此时它的实际权值为2*99999=199998
第三次点亮编号为1的方碑,此时它的实际权值为3*999=2997
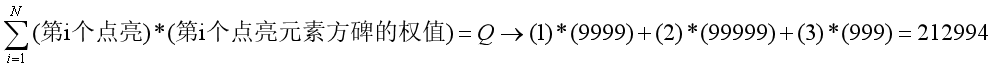
输入格式:
第一行输入一个N(表示这是N个元素方碑的解密),第二行输入一个Q(表示解密成功的实际权值合)。
输出格式:
输出孙俊豪解密成功时依次点亮的方碑编号,相邻两个方碑编号之间用“->”连接。
输入样例1:
3
212994
输出样例1:
2->3->1#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,arr[11],visit[11];
ll a[11]={0,999,9999,99999,999999,9999999,99999999,999999999,9999999999,99999999999,999999999999};
ll qsum,quan;
void dfs(int begin){
if(begin>n){
qsum=0;
for(int i=1;i<=n;i++){
qsum+=i*a[arr[i]];
}
if(qsum==quan){
for(int i=1;i<=n;i++){
if(i>1) cout<<"->";
cout<<arr[i];
}
return ;
}
}else{
for(int i=1;i<=n;i++){
if(visit[i]==0){
arr[begin]=i;
visit[i]=1;
dfs(begin+1);
visit[i]=0;
}
}
}
}
int main()
{
cin>>n>>quan;
dfs(1);
return 0;
}
// #include<bits/stdc++.h>
// using namespace std;
// typedef long long ll;
// ll a[10]={0,999,9999,99999,999999,9999999,99999999,999999999,9999999999,99999999999};
// int main()
// {
// int n,k;
// ll s=0;
// cin>>n;
// for(ll i=1;i<=n;i++){
// cin>>k;
// s+=i*a[k];
// }
// //元素方碑数据构造
// 输入:
// n
// 1 2 3 4
// 输出n个方碑解密-->顺序为1 2 3 4的解密权值和
// cout<<s;
// return 0;
// }原文地址:https://blog.csdn.net/m0_51863774/article/details/134529987
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_11599.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!