1 广度优先搜索
广度优先搜索(Breadth-First Search,BFS)是一种图遍历算法,用于系统地遍历或搜索图(或树)中的所有节点。BFS的核心思想是从起始节点开始,首先访问其所有相邻节点,然后逐层向外扩展,逐一访问相邻节点的相邻节点,以此类推。这意味着BFS会优先探索距离起始节点最近的节点,然后再逐渐扩展到距离更远的节点。BFS通常用于查找最短路径、解决迷宫问题、检测图是否连通以及广泛的图问题。
BFS的工作原理是通过队列数据结构来管理待访问的节点。它从起始节点开始,然后逐一访问该节点的相邻节点,并将它们加入队列。然后,它从队列中取出下一个节点进行访问,以此类推。这确保了节点按照它们的距离从起始节点逐层遍历,因此BFS可以用于查找最短路径。
BFS是一个宽度优先的搜索,它在查找最短路径等问题中非常有用。它不会陷入深度过深的路径,因为它会优先探索距离起始节点更近的节点。
2 应用示例
2.1 迷宫路径搜索
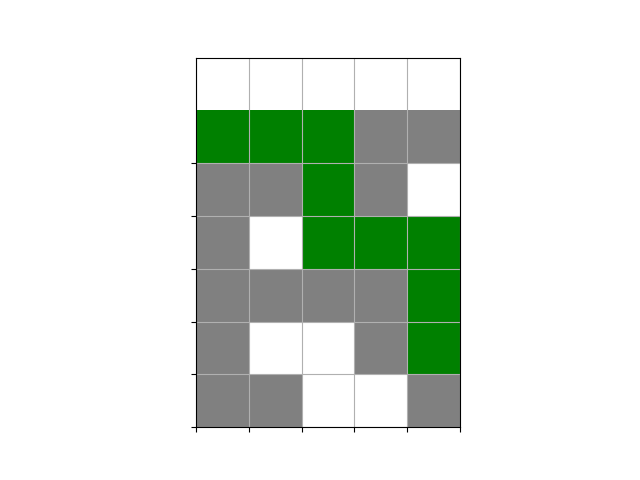
假设有一个迷宫,其中包含墙壁和通道,您希望找到从起始点到终点的最短路径。BFS是解决这类问题的理想选择。
示例迷宫:

S 0 0 1 1 1
1 1 0 1 0 1
1 0 0 0 0 1
1 1 1 1 0 1
1 0 0 1 0 1
1 1 1 1 1 E
S表示起始点E表示终点0表示可以通过的通道1表示墙壁
BFS会优先探索距离
S最近的通道,因此它会找到从S到E的最短路径。在上面的迷宫中,BFS将找到一条最短路径,经过标有数字0的通道,最终到达终点E。这是BFS在寻找最短路径问题中的一个实际应用示例。
示例:
import matplotlib.pyplot as plt
from collections import deque
def bfs_shortest_path(maze, start, end):
# 定义四个方向移动的偏移量,分别是上、下、左、右
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
rows, cols = len(maze), len(maze[0])
# 创建队列用于BFS
queue = deque([(start, [start])])
visited = set()
while queue:
(x, y), path = queue.popleft()
visited.add((x, y))
if (x, y) == end:
return path # 找到了最短路径
for dx, dy in directions:
new_x, new_y = x + dx, y + dy
if 0 <= new_x < rows and 0 <= new_y < cols and maze[new_x][new_y] == 0 and (new_x, new_y) not in visited:
new_path = path + [(new_x, new_y)]
queue.append(((new_x, new_y), new_path))
return None # 没有找到路径
def draw_maze(maze, path=None):
rows, cols = len(maze), len(maze[0])
# 创建一个图形对象
fig, ax = plt.subplots()
# 绘制迷宫
for x in range(rows):
for y in range(cols):
if maze[x][y] == 0:
ax.add_patch(plt.Rectangle((y, -x - 1), 1, 1, facecolor="white"))
else:
ax.add_patch(plt.Rectangle((y, -x - 1), 1, 1, facecolor="gray"))
# 绘制路径(如果存在)
if path:
for x, y in path:
ax.add_patch(plt.Rectangle((y, -x - 1), 1, 1, facecolor="green"))
# 设置坐标轴
ax.set_aspect("equal")
ax.set_xticks(range(cols))
ax.set_yticks(range(-rows, 0))
ax.set_xticklabels([])
ax.set_yticklabels([])
plt.grid(True)
plt.show()
# 示例迷宫,0表示通道,1表示墙壁
maze = [
[0, 0, 0, 1, 1, 1],
[1, 1, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 0, 1],
[1, 0, 0, 1, 0, 0],
[1, 1, 0, 0, 1, 0]
]
start = (0, 0) # 起始点
end = (5, 5) # 终点
path = bfs_shortest_path(maze, start, end)
draw_maze(maze, path)
2.2 社交网络中的关系度排序
广度优先搜索(BFS)的排序应用示例之一是使用它在无权图中查找最短路径。在前面的示例中,我们已经展示了如何使用BFS查找迷宫中的最短路径。这是BFS的一个典型应用示例。
另一个排序应用示例是社交网络中的关系度排序。在社交网络中,您可以使用BFS来确定您与其他用户之间的关系度,即您与其他用户之间的最短路径,或者共同的朋友数量。以下是一个简单的示例:
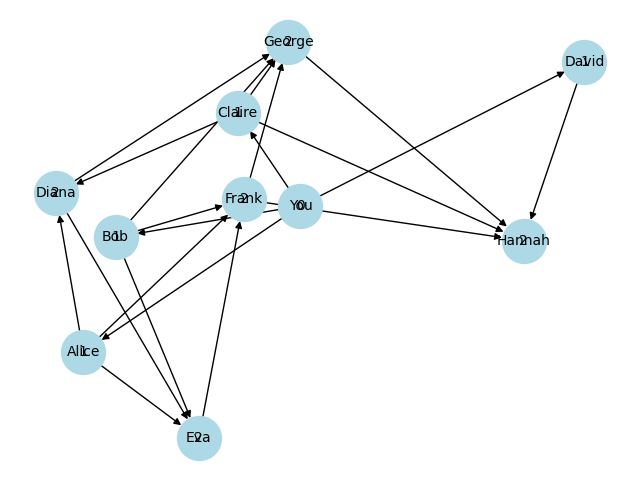
假设您有一个社交网络,其中用户之间的关系用图表示,其中节点代表用户,边代表用户之间的关系。您想知道您与其他用户之间的关系度,并按关系度对用户进行排序。
import networkx as nx
import matplotlib.pyplot as plt
from collections import deque
# 创建一个复杂的社交网络图
social_network = {
'You': ['Alice', 'Bob', 'Claire', 'David'],
'Alice': ['Diana', 'Eva', 'Frank'],
'Bob': ['Eva', 'Frank', 'George'],
'Claire': ['Diana', 'George', 'Hannah'],
'David': ['Hannah'],
'Diana': ['Eva', 'George'],
'Eva': ['Frank'],
'Frank': ['George', 'Hannah'],
'George': ['Hannah'],
'Hannah': [],
}
def bfs_relationship_degree(graph, start):
visited = set()
queue = deque([(start, 0)]) # 用于存储节点和关系度
relationship_degree = {} # 存储关系度
while queue:
node, degree = queue.popleft()
if node not in visited:
visited.add(node)
relationship_degree[node] = degree
for friend in graph[node]:
if friend not in visited:
queue.append((friend, degree + 1))
return relationship_degree
# 使用BFS查找关系度
your_name = 'You'
relationship_degree = bfs_relationship_degree(social_network, your_name)
# 创建一个有向图
G = nx.DiGraph()
# 添加节点和边
for user, degree in relationship_degree.items():
G.add_node(user, degree=degree)
for user in social_network:
for friend in social_network[user]:
G.add_edge(user, friend)
# 绘制图形
pos = nx.spring_layout(G, seed=42)
labels = nx.get_node_attributes(G, 'degree')
nx.draw(G, pos, with_labels=True, node_size=1000, node_color='lightblue', font_size=10, font_color='black')
nx.draw_networkx_labels(G, pos, labels, font_size=10, font_color='black')
plt.title("复杂社交网络图")
plt.show()
# 输出排序结果
sorted_users = sorted(relationship_degree.items(), key=lambda x: x[1])
for user, degree in sorted_users:
print(f'{user}: 关系度 {degree}')
输出:
输出:
You: 关系度 0
Alice: 关系度 1
Bob: 关系度 1
Claire: 关系度 1
David: 关系度 1
Diana: 关系度 2
Eva: 关系度 2
Frank: 关系度 2
George: 关系度 2
Hannah: 关系度 2这段代码的目的是使用广度优先搜索(BFS)算法来查找社交网络中您(’You’)与其他用户之间的关系度,并绘制社交网络图。
首先,定义了一个复杂的社交网络图,其中包括不同用户之间的关系。这个社交网络图存储在
social_network字典中。
bfs_relationship_degree函数实现了BFS算法来查找您与其他用户之间的关系度。它从您开始,逐层查找与您相连接的用户,计算它们之间的关系度。结果存储在relationship_degree字典中。创建一个有向图(DiGraph)
G以绘制社交网络图。添加节点和边到图
G,其中节点代表用户,边代表用户之间的关系。此时,节点的颜色和大小被设置为lightblue和1000,并且边的颜色为gray。运行该代码将绘制出社交网络图,并输出用户的关系度排序结果。这可以帮助您可视化您与其他用户之间的关系,并查看谁与您更亲近。
2.3 查找连通区域
在图像处理中,连通区域是由相邻像素组成的区域,具有相似的特性(如颜色或灰度)。BFS可以用来查找和标记这些连通区域。
import cv2
import numpy as np
# 读取图像
image = cv2.imread('img.jpg', 0) # 以灰度模式读取图像
ret, binary_image = cv2.threshold(image, 127, 255, cv2.THRESH_BINARY)
# 创建一个与图像大小相同的标记图
height, width = binary_image.shape
markers = np.zeros((height, width), dtype=np.int32)
# 定义一个颜色映射
color_map = {
1: (0, 0, 255), # 红色
2: (0, 255, 0), # 绿色
3: (255, 0, 0), # 蓝色
4: (0, 255, 255), # 黄色
# 您可以根据需要添加更多颜色
}
# 连通区域计数
region_count = 0
# 定义8个邻域的偏移
neighbor_offsets = [(-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 1), (1, -1), (1, 0), (1, 1)]
# 开始查找连通区域
for y in range(height):
for x in range(width):
if binary_image[y, x] == 255 and markers[y, x] == 0:
region_count += 1
markers[y, x] = region_count
queue = [(y, x)]
while queue:
current_y, current_x = queue.pop(0)
for dy, dx in neighbor_offsets:
ny, nx = current_y + dy, current_x + dx
if 0 <= ny < height and 0 <= nx < width and binary_image[ny, nx] == 255 and markers[ny, nx] == 0:
markers[ny, nx] = region_count
queue.append((ny, nx))
# 将连通区域标记为不同颜色
result_image = np.zeros((height, width, 3), dtype=np.uint8)
for y in range(height):
for x in range(width):
if markers[y, x] > 0:
result_image[y, x] = color_map[markers[y, x]]
# 显示结果图像
cv2.imshow('Connected Components', result_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
这段代码首先读取了一个灰度图像(也可以使用彩色图像),将其转换为二值图像。然后,它使用BFS算法查找连通区域,对不同的连通区域进行标记,并将它们标记为不同的颜色。最后,它显示带有标记的结果图像。
原文地址:https://blog.csdn.net/qq_35831906/article/details/133859867
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_11755.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!








