本文介绍: 某位著名计算机科学家有句话:“如果智能是蛋糕,无监督学习将是蛋糕本体,有监督学习是蛋糕上的糖霜,强化学习是蛋糕上的樱桃”现在的人工智能大多数应用有监督学习,但无监督学习的世界也是广阔的,因为如今大部分的数据都是没有标签的上一篇文章讲到的降维就是一种无监督学习技术,我们将在本章介绍聚类无监督学习的意义聚类的定义K-Means方法聚类绘制K-Means决策边界。
文章目录
机器学习专栏
无监督学习介绍
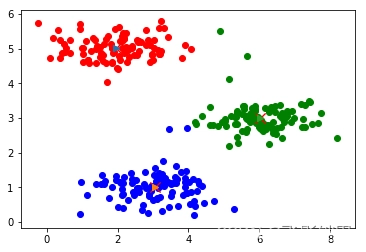
聚类
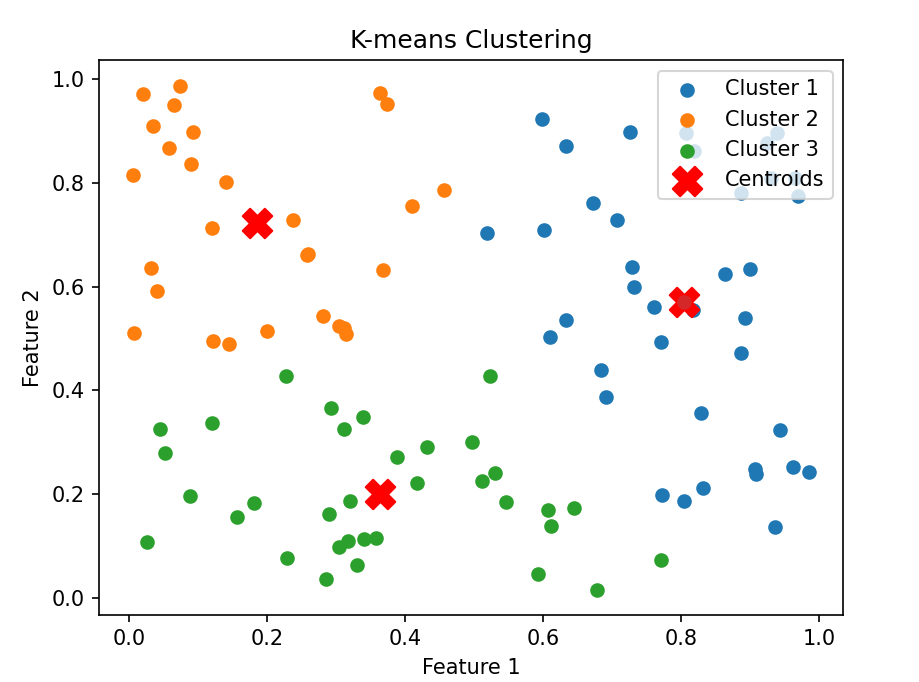
K-Means
使用方法
实例演示
代码解析
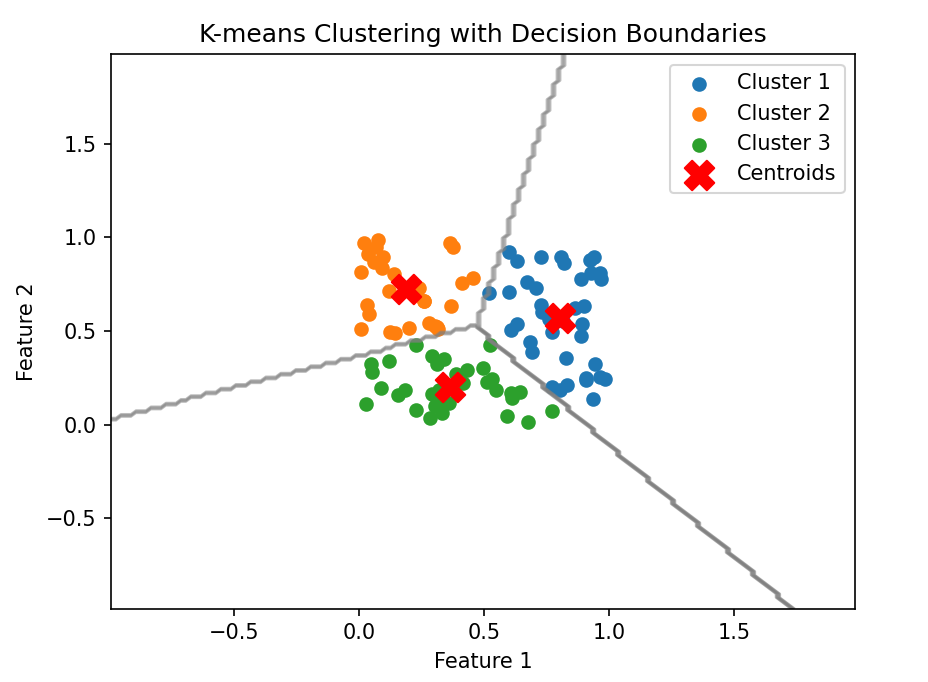
绘制决策边界
本章总结
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。