本文介绍: 考虑这样一个场景,如何统计一个大型网站的去重日活、月活用户(UV)?你可以通过 set 集合、bitmap 这类常用工具,但有个最大的缺点是,如果数据量巨大,比如 1 亿,甚至 10 亿将耗费巨大内存消耗。有人研究出了这样一种算法叫 `HyperLogLog`,是一种概率性的统计算法,每个 `HyperLogLog` 对象最大占用空间为 `12KB`,相当节省内存。你应该也猜到了,这么小的内存消耗,是无法记录真实的明细数据,统计数值也不是完全精准,有一定的误差比例。
前言
考虑这样一个场景,如何统计一个大型网站的去重日活、月活用户(UV)?
你可以通过 set 集合、bitmap 这类常用工具,但有个最大的缺点是,如果数据量巨大,比如 1 亿,甚至 10 亿将耗费巨大内存消耗。
有人研究出了这样一种算法叫 HyperLogLog,是一种概率性的统计算法,每个 HyperLogLog 对象最大占用空间为 12KB,相当节省内存。
你应该也猜到了,这么小的内存消耗,是无法记录真实的明细数据,统计数值也不是完全精准,有一定的误差比例。
一、动手试试?
redis HyperLogLog 主要提供了三个操作:PFADD、PFCOUNT、PFMERGE,分别用于添加、计数与合并。
1. 添加
2. 统计
3. 合并
二、原理
1. 伯努利过程
2. HyperLogLog
2.1 工作原理
2.2 占用内存大小
2.3 内存优化?
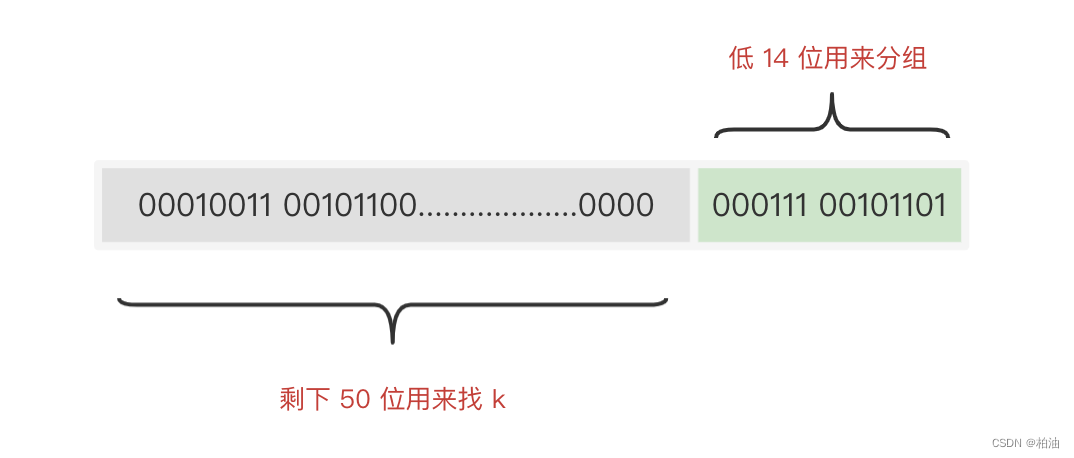
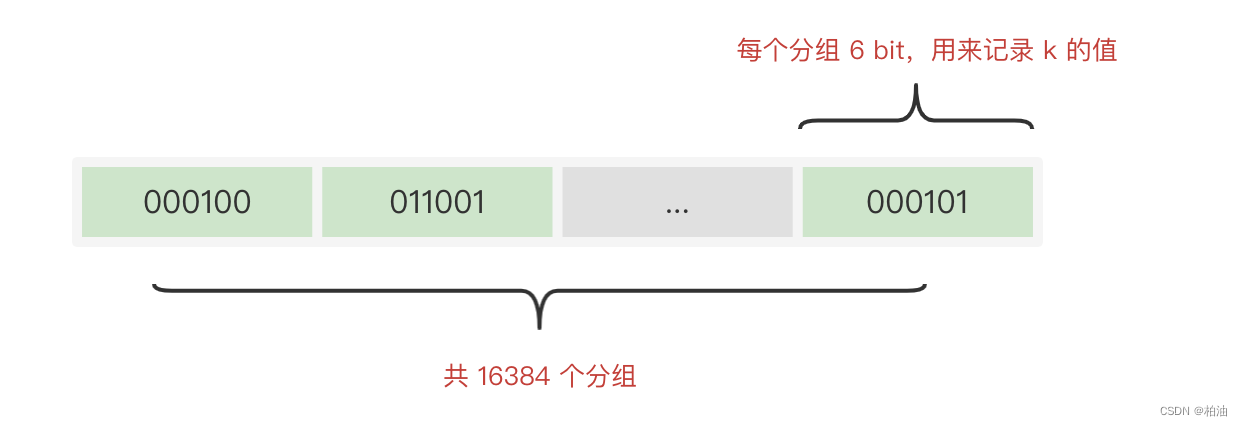
3. 数据编码
3.1 稀疏编码
3.2 密集编码
3.3 转码
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。





![[软件工具]文档页数统计工具软件pdf统计页数word统计页数ppt统计页数图文打印店快速报价工具](https://img-blog.csdnimg.cn/direct/09dfbaff3e9a47a9a551dd65fef5d482.jpeg)