LeetCode 106. 从中序与后序遍历序列构造二叉树——数据结构

本文介绍: 给定两个整数数组 inorder和postorder，其中inorder是二叉树的中序遍历，postorder是同一棵树的后序遍历，请你构造并返回这颗二叉树。**输入：**inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]**输入：**inorder = [-1], postorder = [-1][-1]postorder postorder inorder in order postorder。

106. 从中序与后序遍历序列构造二叉树

labuladong 题解思路

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

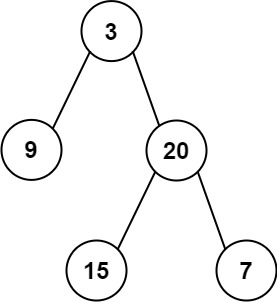
**输入：**i nor der = [9,3,15,20,7], p os torder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

**输入：**i norder = [-1], p os torder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由不同的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

题解

为了根据中序遍历（inorder）和后序遍历（postorder）重建二叉树，我们可以利用中序和后序遍历的特性：

中序遍历 inorder 的顺序是 左子树-根节点-右子树。
后序遍历 postorder 的顺序是 左子树-右子树-根节点。

重建的基本思路是使用后序遍历的最后一个元素确定根节点，然后根据这个根节点将中序遍历分割为左右子树。接着对左右子树递归地进行同样的操作。

以下是 C++ 中的实现：

class TreeNode {
public:
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    TreeNode* buildTree(vector<int&gt;&amp; inorder, vector<int&gt;&amp; postorder) {
        return buildTreeHelper(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }

    TreeNode* buildTreeHelper(vector<int&gt;&amp; inorder, int i_start, int i_end, vector<int&gt;&amp; postorder, int p_start, int p_end) {
        if (p_start == p_end) {
            return nullptr;
        }
        int root_val = postorder[p_end - 1];
        TreeNode* root = new TreeNode(root_val);

        int i_root_index = 0;
        for (int i = i_start; i < i_end; i++) {
            if (inorder[i] == root_val) {
                i_root_index = i;
                break;
            }
        }

        int left_num = i_root_index - i_start;
        root->left = buildTreeHelper(inorder, i_start, i_root_index, postorder, p_start, p_start + left_num);
        root->right = buildTreeHelper(inorder, i_root_index + 1, i_end, postorder, p_start + left_num, p_end - 1);
        
        return root;
    }
};

算法说明：

从 postorder 中取出最后一个元素，这是当前的根节点。
在 inorder 中找到这个根节点的位置，这将中序遍历分割为左右子树。
对左右子树递归地执行上述过程。
构建当前的根节点，并将其左右子树分别设置为递归调用返回的结果。
返回构建的树的根节点。

问：left_num是干什么的？
答：在提供的代码中，left_num 用于计算中序遍历数组 inorder 中根节点左侧的元素数量，即左子树的节点数量。这个值非常关键，因为它帮助我们在递归过程中正确地划分中序和后序遍历数组，从而构造出正确的左子树和右子树。

具体来说，left_num 的作用如下：

划分中序遍历数组：在中序遍历数组 inorder 中，根节点左侧的所有元素都属于左子树，右侧的所有元素属于右子树。left_num 指示了左子树元素的数量，因此我们可以使用 left_num 将中序遍历数组分为左右两部分。
划分后序遍历数组：在后序遍历数组 postorder 中，前 left_num 个元素对应于左子树的后序遍历，其余元素（除了最后一个元素，即当前的根节点）对应于右子树的后序遍历。

下面是如何使用 left_num 划分这两个数组的示例：

int left_num = i_root_index - i_start;
root->left = buildTreeHelper(inorder, i_start, i_root_index, postorder, p_start, p_start + left_num);
root->right = buildTreeHelper(inorder, i_root_index + 1, i_end, postorder, p_start + left_num, p_end - 1);

在这段代码中，buildTreeHelper 函数被两次调用，一次用于构建左子树，一次用于构建右子树：

左子树：inorder 数组中从 i_start 到 i_root_index 的部分，postorder 数组中从 p_start 到 p_start + left_num 的部分。
右子树：inorder 数组中从 i_root_index + 1 到 i_end 的部分，postorder 数组中从 p_start + left_num 到 p_end - 1 的部分。