本文介绍: 此处代码就开始简化了:时间复杂度为O(N),先用上等差数列的公式求前num个数字之和,再一一减去nums数组中的元素,最后得到的就是消失的数字!0^1^2^…中间有消失的数…^n ^1^2^…中间消失的数不在这里…^n = 0^中间有消失的数 =思路:用0先跟0~numsSize中数据异或,再跟nums数组中所有元素异或,最后的值就是所要找的值。3.满足交换律,如:(a^b) ^ c =a^(b^c)这个操作符是对二进制来用的,相同为零相异为一。此处不建议使用该方法,因为时间复杂度过大。
一、消失的数字
思路一(暴力求解)代码实现:
思路二(数列的思想)代码实现:
思路三(异或的运用)代码实现:
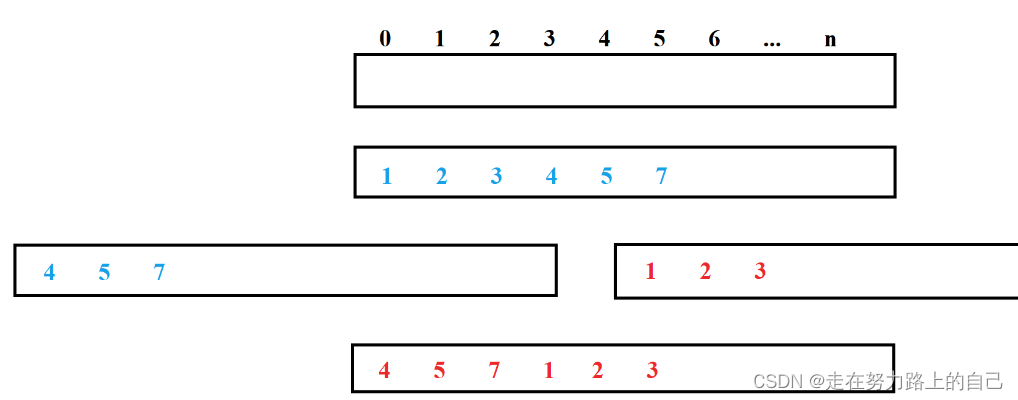
二、轮转数组
思路一(暴力求解)代码实现:
思路二使用额外的空间(以空间换时间)代码实现:
思路三(三步逆置)
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。










![[软件工具]文档页数统计工具软件pdf统计页数word统计页数ppt统计页数图文打印店快速报价工具](https://img-blog.csdnimg.cn/direct/09dfbaff3e9a47a9a551dd65fef5d482.jpeg)