1. 一元多项式拟合
使用方法 np.polyfit(x, y, deg)
polyfig 使用的是最小二乘法,用于拟合一元多项式函数。
参数说明: x 就是x坐标,y 就是y坐标,deg 为拟合多项式的次数。
实例:
根据 ti yi 两个列表来得到 一元二次多项式拟合函数 (deg为2)
import matplotlib.pyplot as plt
import numpy as np
import pylab as mpl
ti = [1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6, 6.5, 7, 7.5, 8]
yi = [33.40, 79.50, 122.65, 159.05, 189.15, 214.15, 238.65, 252.2, 267.55, 280.50, 296.65, 301.65, 310.4, 318.15, 325.15]
z1 = np.polyfit(ti, yi, 2)
print(z1)分别是二次多项式的 3 个系数,y = ax^2 + bx + c

2. 任意函数拟合
使用 curve_fit() 方法
curve_fit() 使用是非线性最小二乘法将函数进行拟合,适用范围:多元、任意函数
scipy.optimize.curve_fit(f,xdata,ydata,p0 = None)常用参数说明:
f: 模型函数f(x,…)。它必须将自变量作为第一个参数,其余你需要求的参数都放后面
xdata: 数组对象,测量数据的自变量。
ydata: 数组对象,因变量。
p0:参数的初始猜测(长度 N),如果为None,则初始值为1(如果可以使用自省来确定函数的参数数量,否则会引发 ValueError)。返回值:
popt: 数组,参数的最佳值,以使的平方残差之和最小。f(xdata, *popt) - ydata
pcov: 二维阵列,popt的估计协方差。对角线提供参数估计的方差。实例:
(1)初始化 x 和 y 数据集
x 为 0~19(包括0和19),y=2x^2 + (二十个0~100范围内的随机数)
import numpy as np
x = np.arange(0,20)
y = 2 * x ** 2 + np.random.randint(0, 100, 20)
#z = 2 * x ** 2 + np.random.randint(0, 100, (1,20))[0]
numpy.random.randint(low, high=None, size=None, dtype=int)
参数说明:
1. low: int 生成的数值的最小值(包含),默认为0,可省略。
2. high: int 生成的数值的最大值(不包含)。
3. size: int or tuple of ints 随机数的尺寸, 默认是返回单个,输入 20 返回 20个,输入 (3,4) 返回的是一个 3*4 的二维数组。(可选)。
4. dtype:想要输出的结果类型。默认值为int。(可选,一般用不上)。
(2)建立自定义函数
定义函数 y=ax^2
#变量一定要放在第一个位置
def func(x, a):
return a*x**2
popt, pcov = curve_fit(func, x, y, p0=1) #p0 = 1是因为只有a一参数
print(popt) #即参数a的最佳值
print(pcov)输出结果:

#变量一定要放在第一个位置
def func(x, a, b, c):
return a*x**2 + b*x + c
popt, pcov = curve_fit(func, x, y) #p0 = 1是因为只有a一参数
print(popt) #即参数a的最佳值
print(pcov)输出结果:

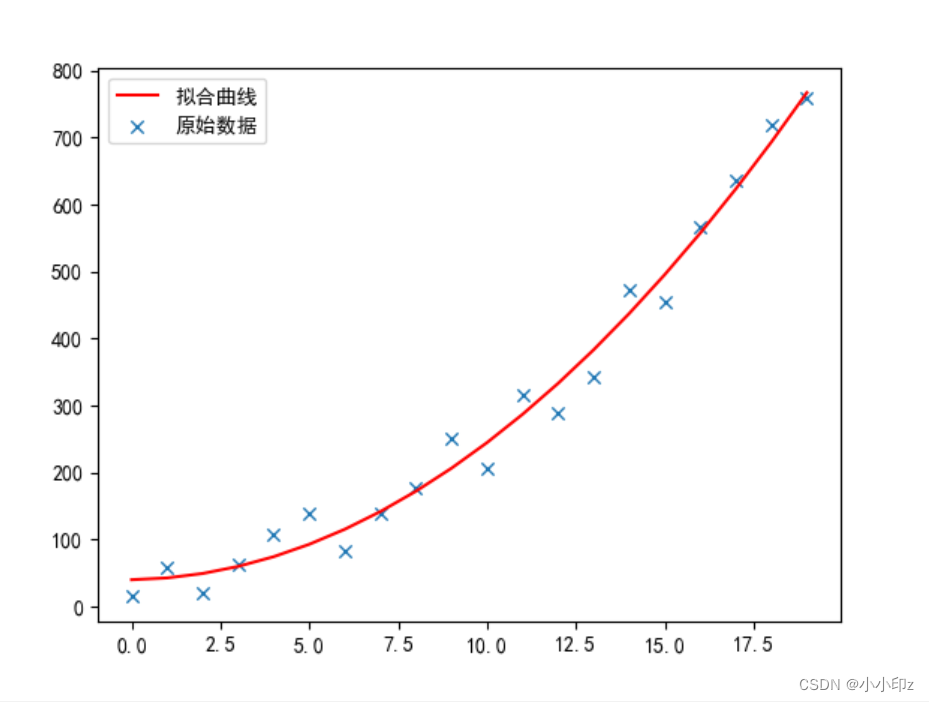
(3)使用自定义的函数生成拟合函数绘图
完整代码:
注意:在画图是可能会出现坐标中文乱码的问题,需要加入以下几行:
mpl.rcParams[‘font.sans-serif’] = [‘SimHei’] # 解决中文不显示问题 plt.rcParams[‘axes.unicode_minus’]=False #解决负数坐标显示问题
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import pylab as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文不显示问题
plt.rcParams['axes.unicode_minus']=False #解决负数坐标显示问题
x = np.arange(0,20)
y = 2 * x ** 2 + np.random.randint(0, 100, 20)
z = 2 * x ** 2 + np.random.randint(0, 100, (1,20))[0]
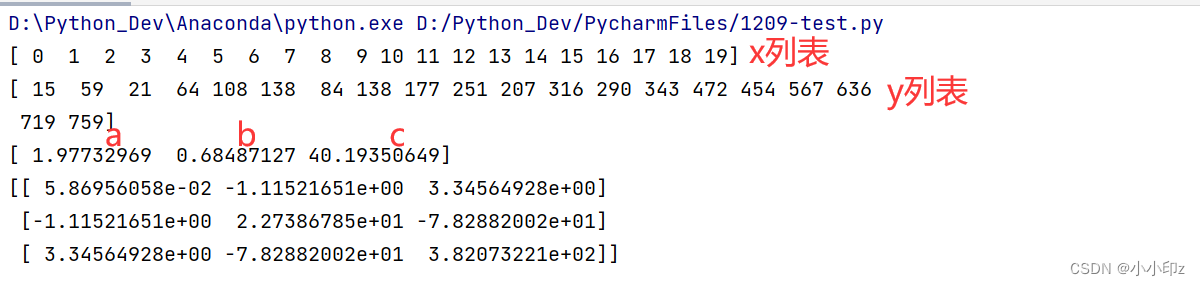
print(x)
print(y)
#变量一定要放在第一个位置
def func(x, a, b, c):
return a*x**2 + b*x + c
popt, pcov = curve_fit(func, x, y) #p0 = 1是因为只有a一参数
print(popt) #即参数a的最佳值
print(pcov)
#popt[0],popt[1],popt[2]分别代表参数a b c
y2 = func(x,popt[0],popt[1],popt[2])
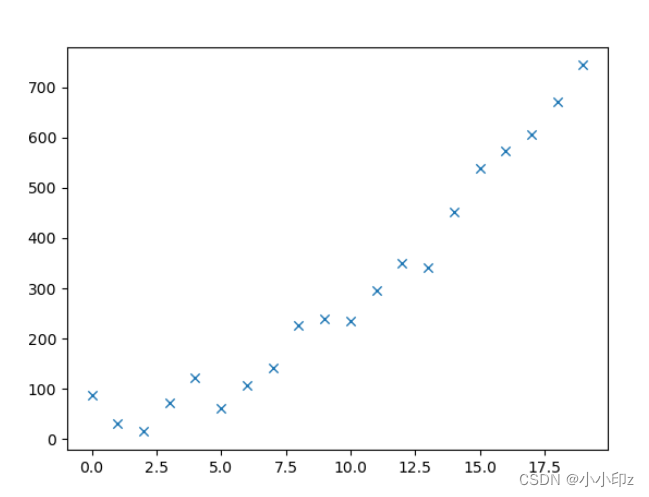
plt.scatter(x, y, marker='x',lw=1,label='原始数据')
plt.plot(x,y2,c='r',label='拟合曲线')
plt.legend() # 显示label
plt.show()运行结果:
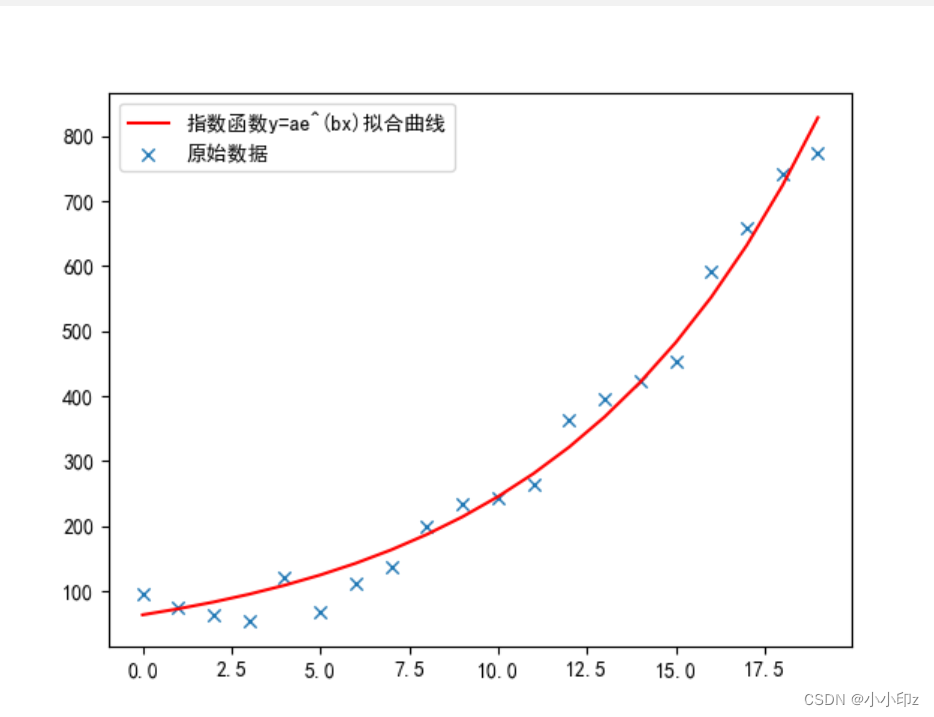
使用指数函数:
y = ae^(bx)

绘图效果:
原文地址:https://blog.csdn.net/weixin_49561506/article/details/128256485
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_13901.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!