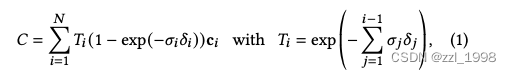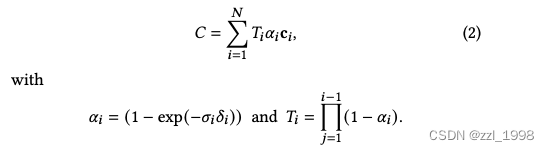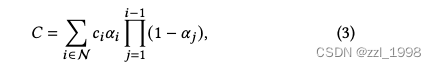本文介绍: NeRF效果好,但是训练和渲染很花时间;特别是对1080p分辨率渲染的场景,现有方法无法实现实时渲染。本文引入三个关键部分,实现sota视觉质量、较短训练时间和1080p分辨率下新视角实时渲染。。通过camera calibration中产生的稀疏点进行初始化。这种新的3D表达形式在保存NeRF优点的同时,避免了空白空间不必要的计算开销;。实现3D Gaussian的交替优化和密度控制,优化各向异性协方差矩阵实现对场景的准确表达;Rendering。

摘要
引言
近期工作
Traditional Scene Reconstruction and Rendering
Neural Rendering and Radiance Fields
Point-Based Rendering and Radiance Fields
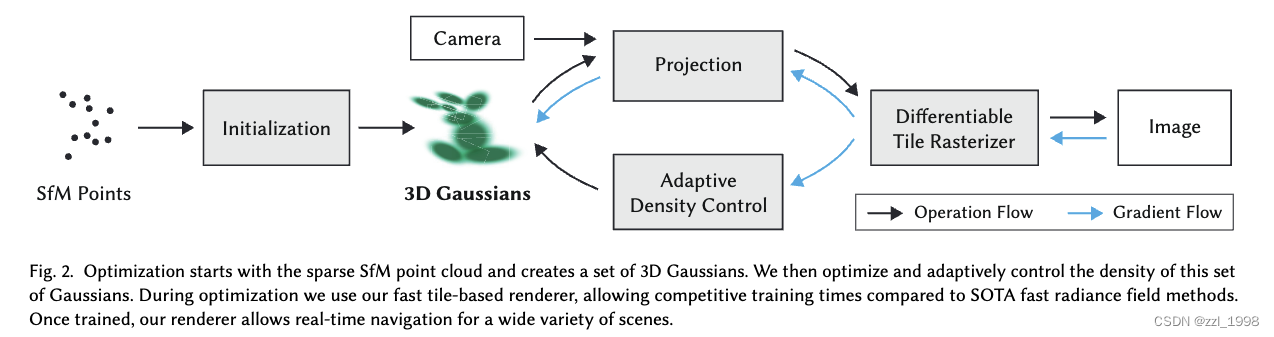
Overview
Differentiable 3D Gaussian Splatting
Optimization with Adaptive Density Control of 3D Gaussians
Fast Differentiable Rasterizer for Gaussians
Implementation, Results and Evaluation
Implementation
Results and Evaluation
Real-World Scenes
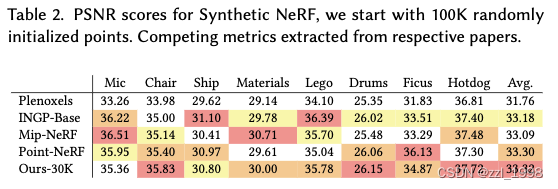
Synthetic Bounded Scenes
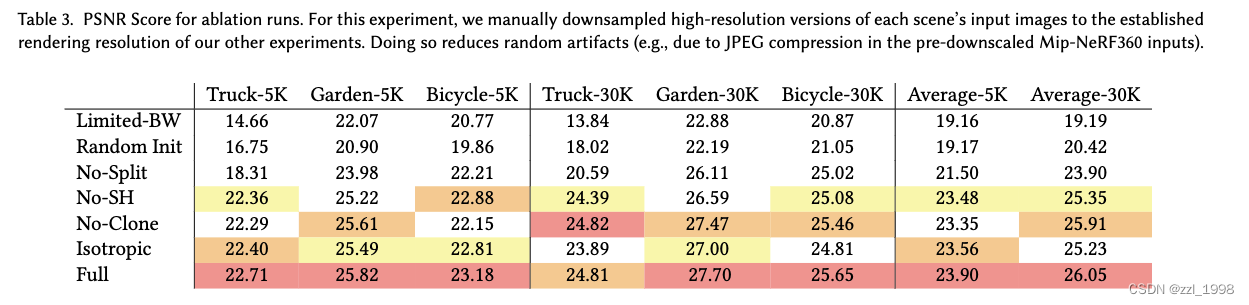
Ablations
Initialization from SfM
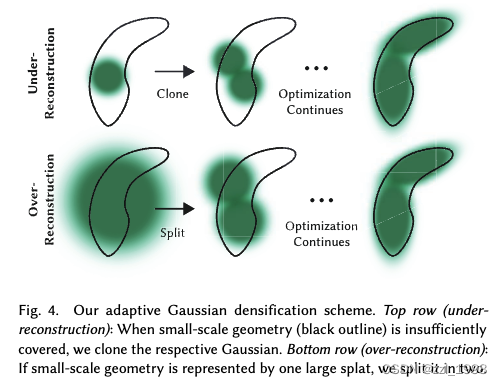
Densification
Unlimited depth complexity of splats with gradients
Anisotropic Covariance
Limitations
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。