LeetCode51. N-Queens

文章 目录

- 一、题目
- 二、题解

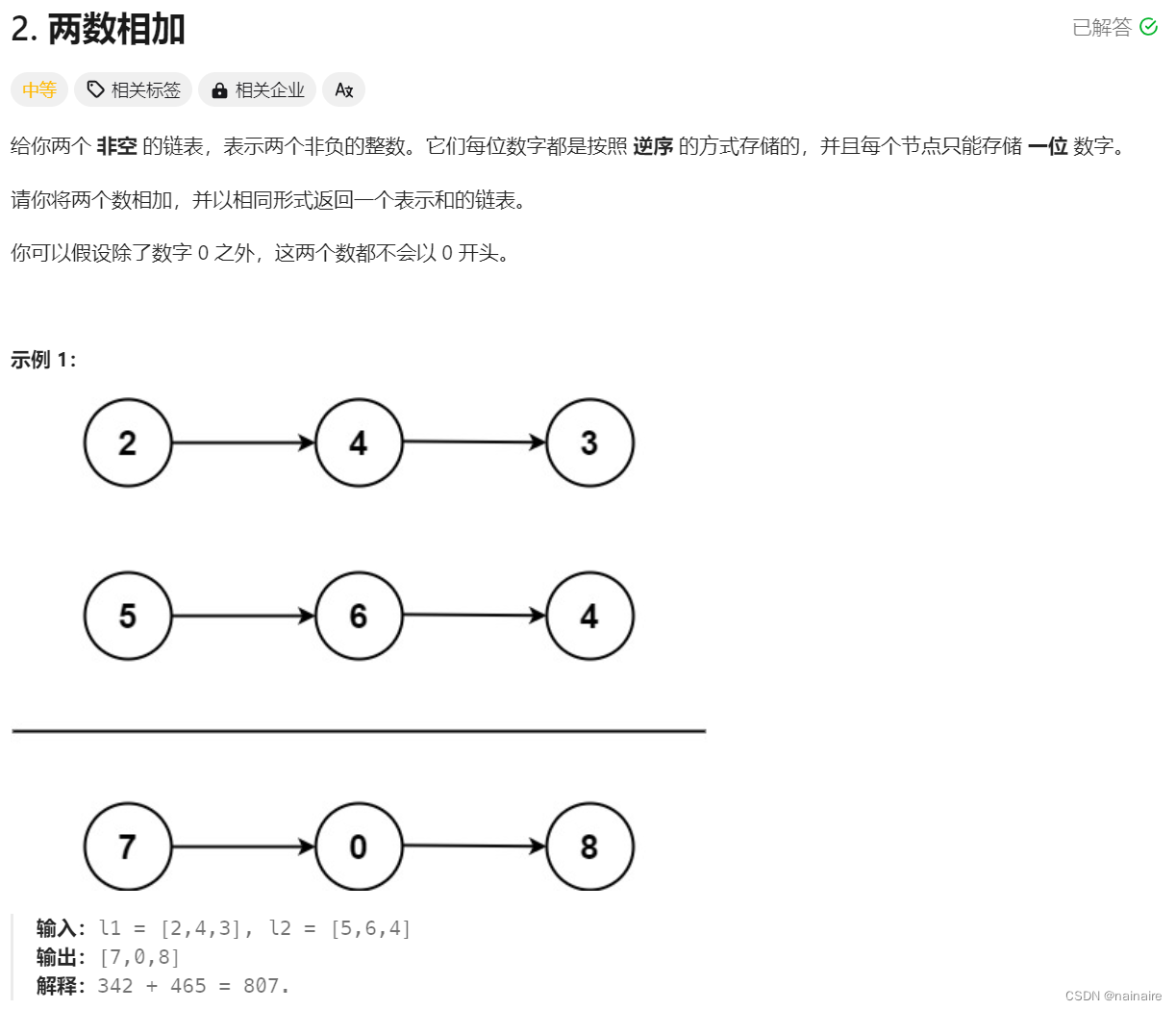
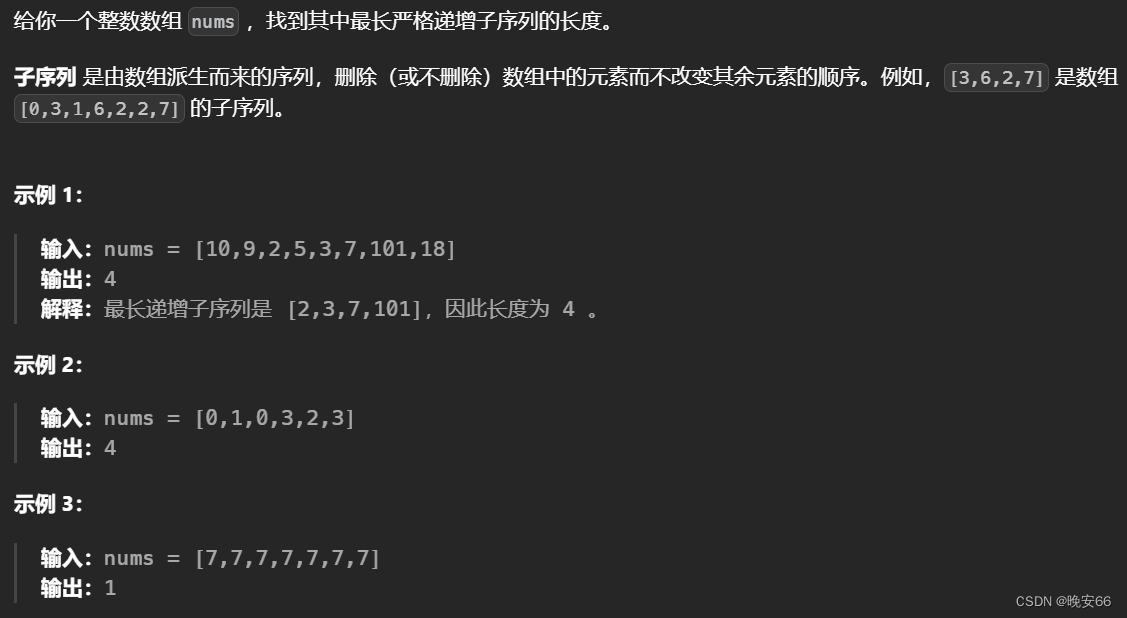
一、题目

Th e n-queens puzzle i s t h e pro blem of pla cing n queens on an n x n ch es s boar d su ch t ha t no two queens attack each oth e r.

Gi v en an integer n, return all distinct solutions to th e n-queens puzzle. You may return the answ e r in any order.

Each solution contain s a distinct boar d configuration of the n-queens’ place ment, where ‘Q’ and ‘.’ both indicate a queen and an empty space, r especti v ely.

Ex ample 1:

Input: n = 4
Output: [[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
Explanation: There ex i st two distinct solutions to the 4-queens puzzle as shown above
Ex ample 2:

Input: n = 1
Output: [[“Q”]]

Con s train ts:

1 <= n <= 9

二、题解

class Solution {
public:
    vector<vector<string&gt;&gt; res;
    bool isValid(vector<string&gt;&amp; chessboard,int row,int col,int n){
        //检查列
        for(int i = 0;i < row;i++){
            if(chessboard[i][col] == 'Q') return false;
        }
        //检查45度角
        for(int i = row - 1,j = col - 1;i &gt;= 0 &amp;&amp; j >= 0;i--,j--){
            if(chessboard[i][j] == 'Q') return false;
        }
        //检查135度角
        for(int i = row - 1,j = col + 1;i >= 0 &amp;&amp; j < n;i--,j++){
            if(chessboard[i][j] == 'Q') return false;
        }
        return true;
    }
    void backtracing(vector<string>&amp; chessboard,int row,int n){
        if(row == n){
            res.push_back(chessboard);
            return;
        }
        for(int i = 0;i < n;i++){
            if(isValid(chessboard,row,i,n)){
                chessboard[row][i] = 'Q';
                backtracing(chessboard,row+1,n);
                chessboard[row][i] = '.';
            }
        }
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<string> chessboard(n,string(n,'.'));
        backtracing(chessboard,0,n);
        return res;
    }
};