本文介绍: PCA的用处:找出反应数据中最大变差的投影(就是拉的最开)。在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的但是什么时候信息保留的最多呢?具体一点?首先:去中心化(把坐标原点放到数据中心,如上图所示)然后,找坐标系(找到方差最大的方向)问题是:怎么找到方差最大的方向呢????????
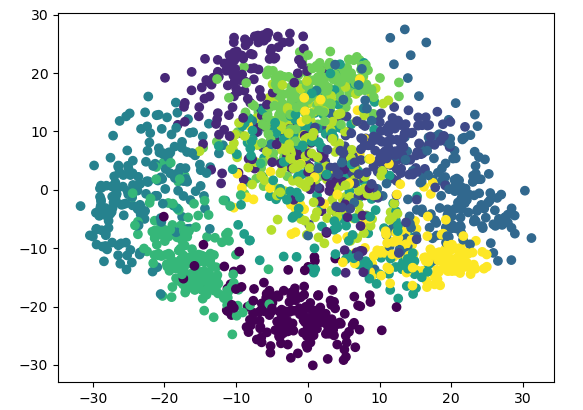
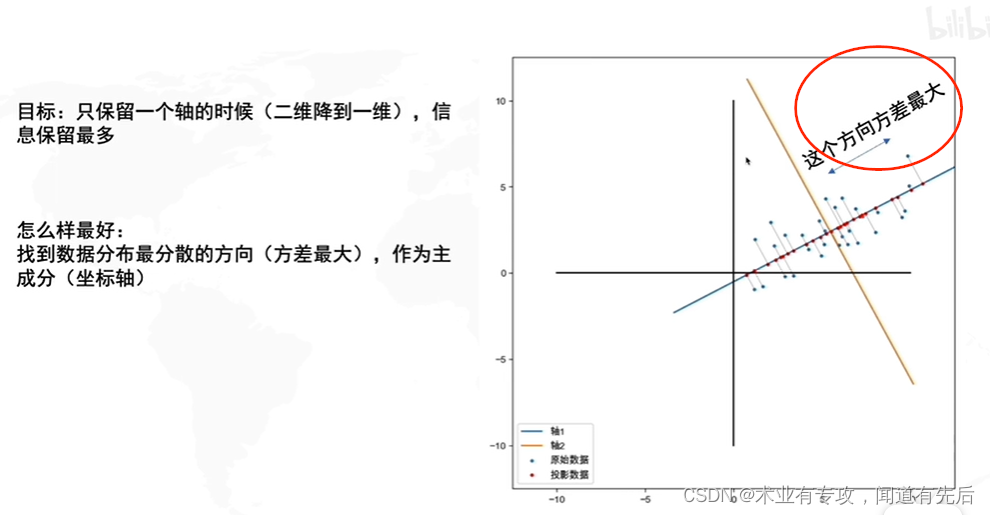
PCA的用处:找出反应数据中最大变差的投影(就是拉的最开)。
在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的
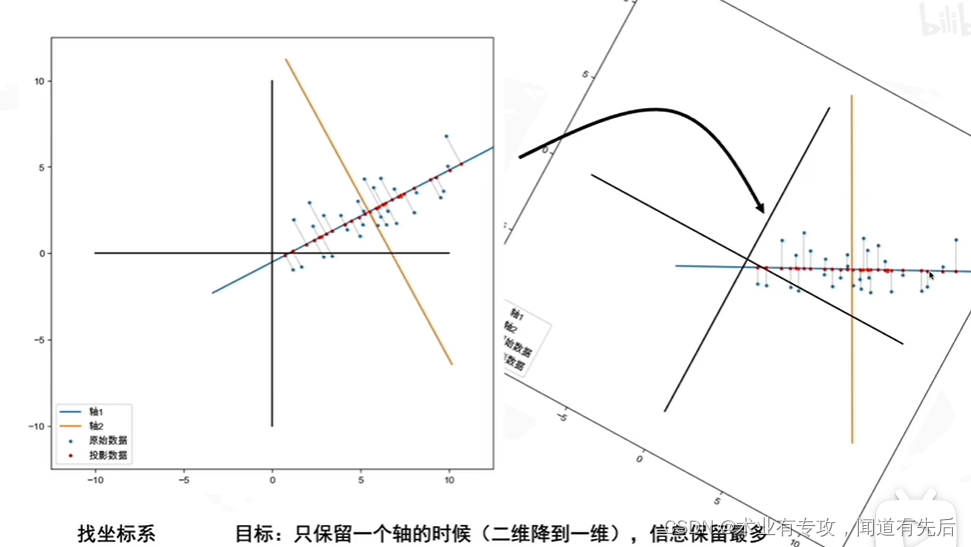
但是什么时候信息保留的最多呢?具体一点?

一.引子
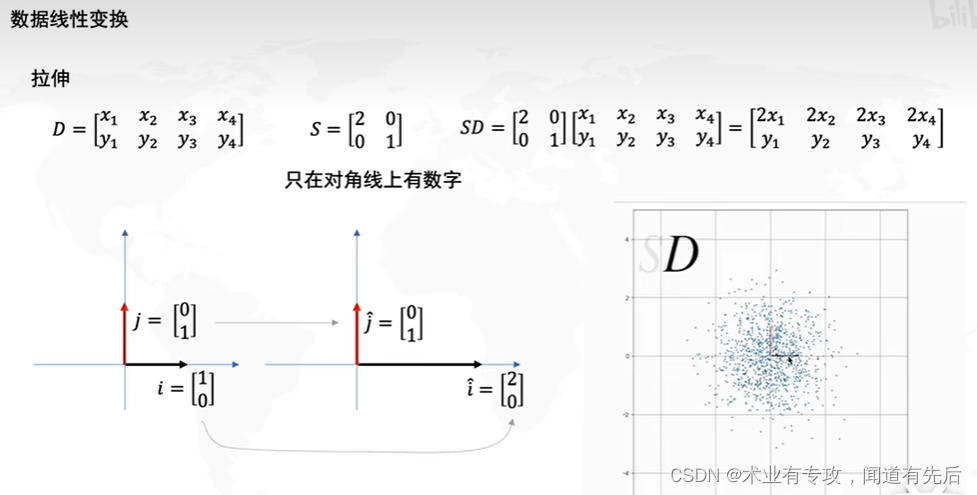
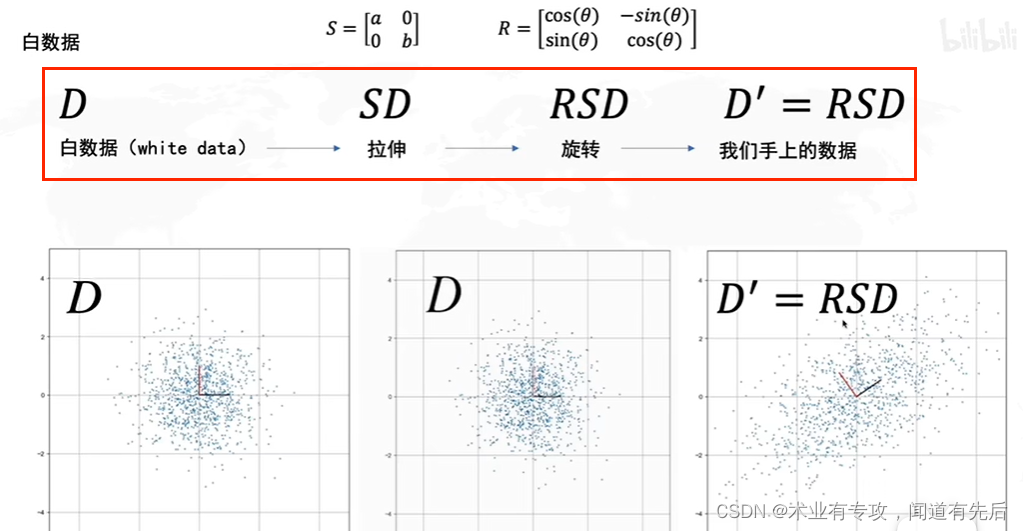
二.数学原理:
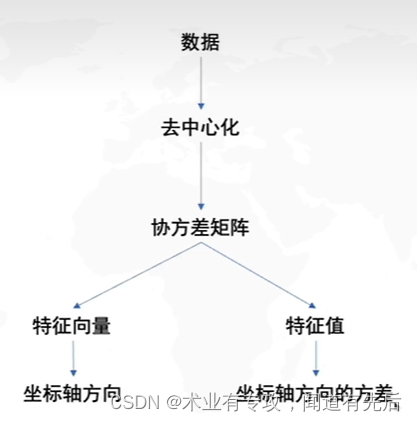
三.PCA流程图:
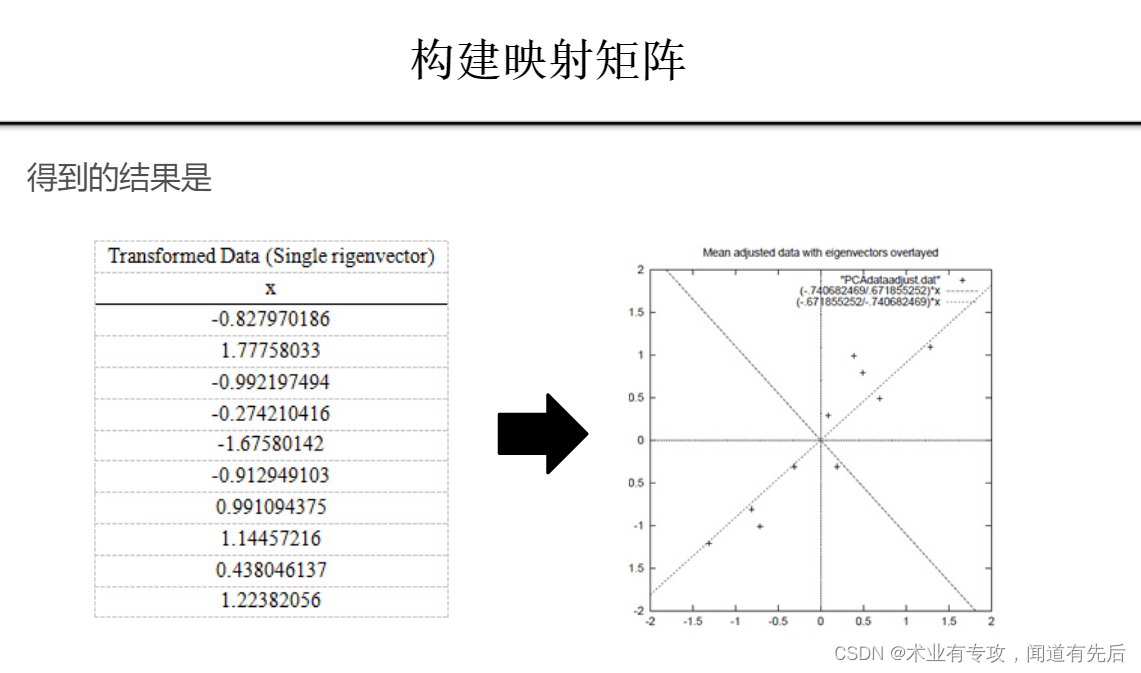
四.例子:
五.代码:
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。










![[PyTorch][chapter 5][李宏毅深度学习][Classification]](http://www.7code.cn/wp-content/themes/ripro-v2/assets/img/thumb-ing.gif)