本文介绍: 解释:我们无法移除任何一个元素使得和被 9 整除,最优方案是移除子数组 [5,2] ,剩余元素为 [6,3],和为 9。我们可以移除子数组 [4] ,剩余元素的和为 6。输入:nums = [1000000000,1000000000,1000000000], p = 3。输入:nums = [3,1,4,2], p = 6。输入:nums = [6,3,5,2], p = 9。输入:nums = [1,2,3], p = 3。输入:nums = [1,2,3], p = 7。,值就是其对应的下标。
题目链接
题目描述
n
u
示例 1:
示例 2:
提示3:
提示4:
提示5:
提示:
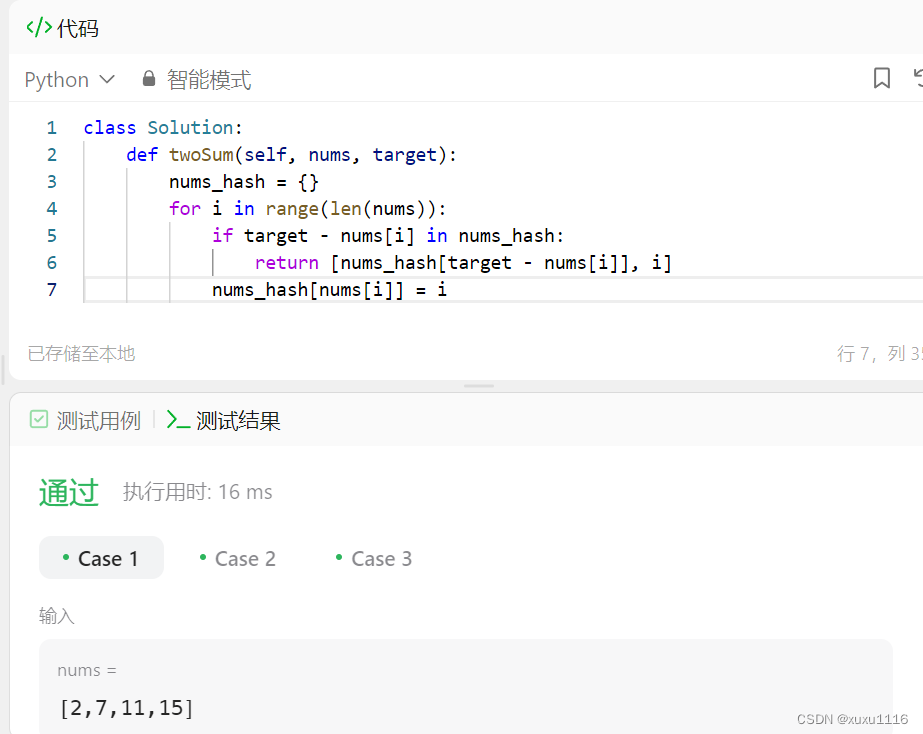
解法:前缀和 + 哈希表
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。