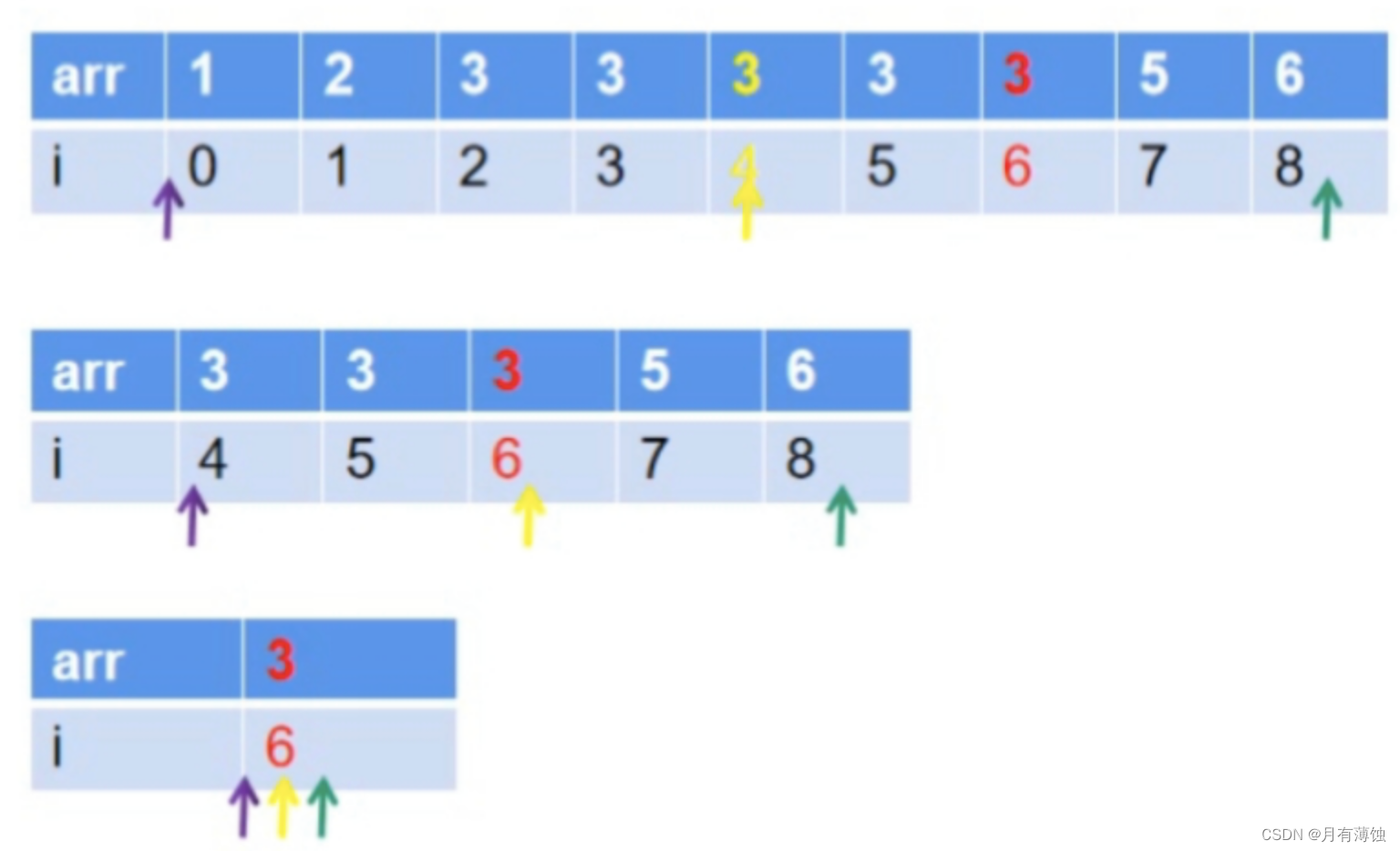
本文介绍: 此时区间变为[0,4],既保证了下标为4的2保留在区间里,又保证可以继续查找[0,4]中是否还有数字2,如果[0,3]中没有数字2了,则下标4就会是该区间唯一一个满足条件的值,也就会是最终结果。而如果[0,3]中还有其他的2,就如本例,那么下标为4的数字就会被下一次缩小区间所抛弃。另一种退出循环的方式就是l>r,l跑到r的右边,那么不管怎么说,l都不可能是最终目标。判断r是否是x:如果退出循环后a[r]==x,说明找到了x,并且这个x是左边界的x;接下来 q行,每行包含一个整数 k,表示一个询问元素。
二分
一、整数二分
(一)整数二分思路
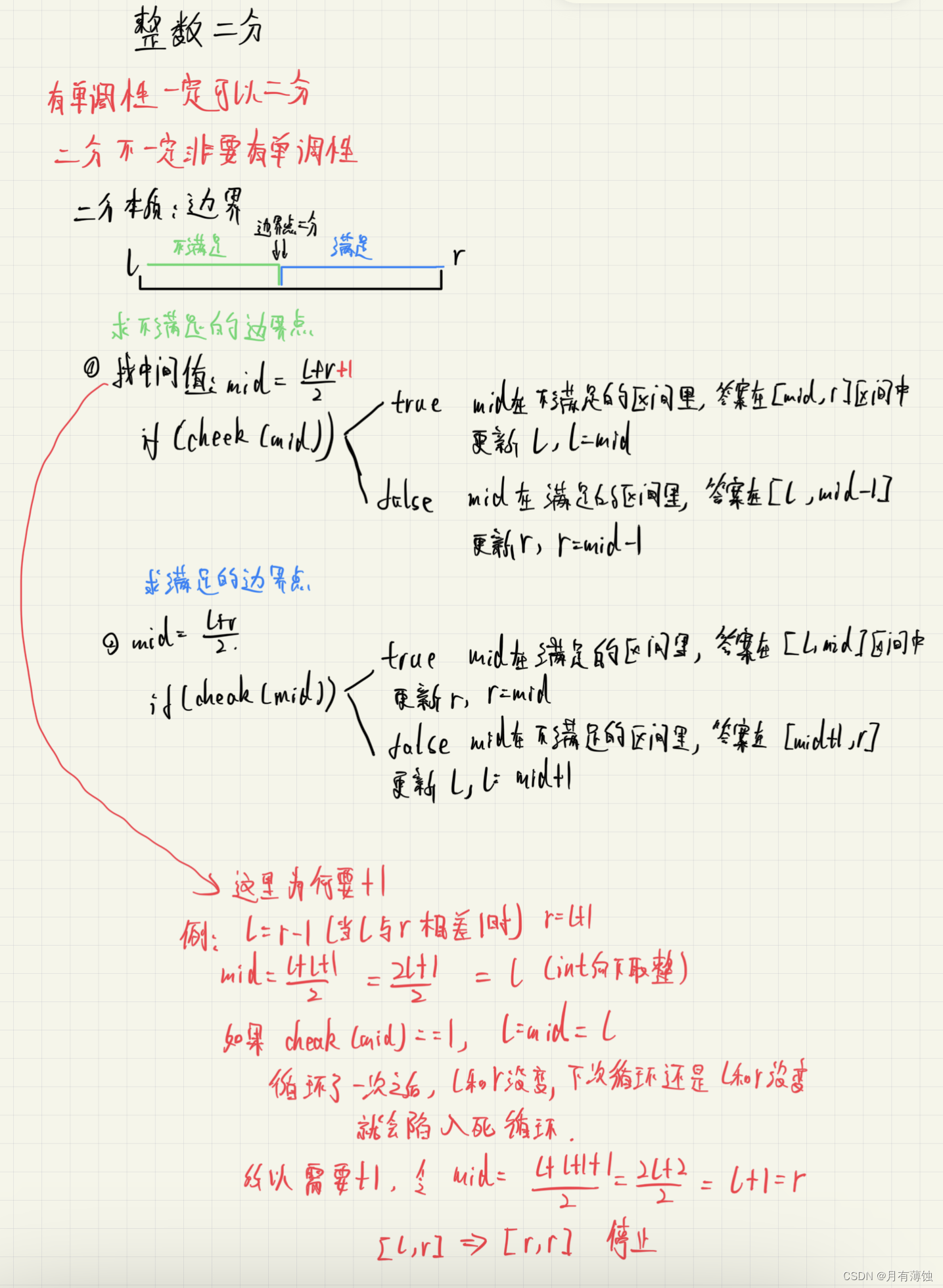
(二)整数二分算法模板
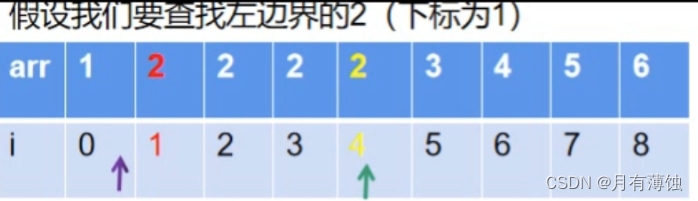
1.左查找(寻找左侧边界)
我们可以将等于和大于的情况合二为一,因为不管怎样最终都是要判断r是否为目标值的。所以,升级后的代码如下。
2.右查找(寻找右侧边界)
3.总模板
(三)题目:数的范围
给定一个按照升序排列的长度为 n的整数数组,以及 q个查询。对于每个查询,返回一个元素 k的起始位置和终止位置(位置从 0开始计数)。如果数组中不存在该元素,则返回 -1 -1。
二、浮点数二分
(一)浮点数二分思路
(二)浮点数二分算法模板
(三)题目:数的三次方根
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。