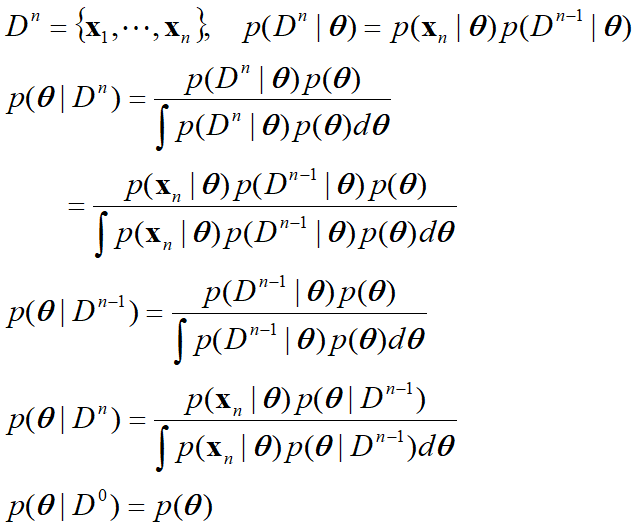本文介绍: 最大似然估计将参数看作是确定的量,只是其值是未知!通过最大化所观察的样本概率得到最优的。贝叶斯方法把参数当成服从某种先验概率分布的随机变量,对样本进行观测的过程,就是把先验概。率密度转化成为后验概率密度,使得对于每个新样本,后验概率密度函数在待估参数的真实值附近。如果可以将类条件密度参数化,则可以显著降低难度。在以下条件下我们可以设计一个可选择的分类器。在参数估计完后,两种方法都用后验概率。),用两个参数表示,这样就。贝叶斯框架下的数据收集,的正态性,P(x | w。但是方法本质是不同的。
1. 估计
贝叶斯框架下的数据收集,在以下条件下我们可以设计一个可选择的分类器 :
②对类条件密度的估计存在两个问题:1)样本对于类条件估计太少了;2) 特征空间维数太大
2. 最大似然估计
2.1 基本原理
2.2 高斯情况:μ未知
2.3 高斯情况:μ和Σ未知
3. 贝叶斯估计
3.1 类条件密度
3.2 参数分布
3.3 高斯过程
4. 贝叶斯参数估计一般理论
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。




















 。
。